考虑交叉耦合因素的IPMSM无传感器改进线性自抗扰控制策略
- 一级目录
- 二级目录
- 三级目录
- 控制原理
- ELADRC
- 信号提取
- 龙格贝尔观测器
- 方波注入
- simulink仿真
- 给定转速:
- 转速环:
- 电流环:
一级目录
二级目录
三级目录
首先声明一下,本篇博客是复现IEEE文章Enhanced Linear ADRC Strategy for Sensorless
Control of IPMSM Considering Cross-Coupling Factors
仅供参考
利用高频信号注入估计转子坐标系是一种有效的无传感器控制策略,可解决内装永磁同步电机低速范围内位置信息的解耦问题。但磁饱和引起的电感交叉耦合现象会导致转子角度提取精度下降,导致无传感器控制性能严重恶化。为了解决这一问题,提出了一种考虑d-q轴耦合电感的高频信号注入方法来估计高频电感和转子角度。在电流环控制中采用估计高频电感和电流环增强型线性自抗扰控制相结合的方法来估计干扰,提高电流控制系统的电流调节质量。在此基础上,从理论上分析了改进型**LADRC的稳定性和跟踪性能。**最后,分析了考虑高频电感的基于ELADRC的闭环IPMSM驱动系统的稳定性。
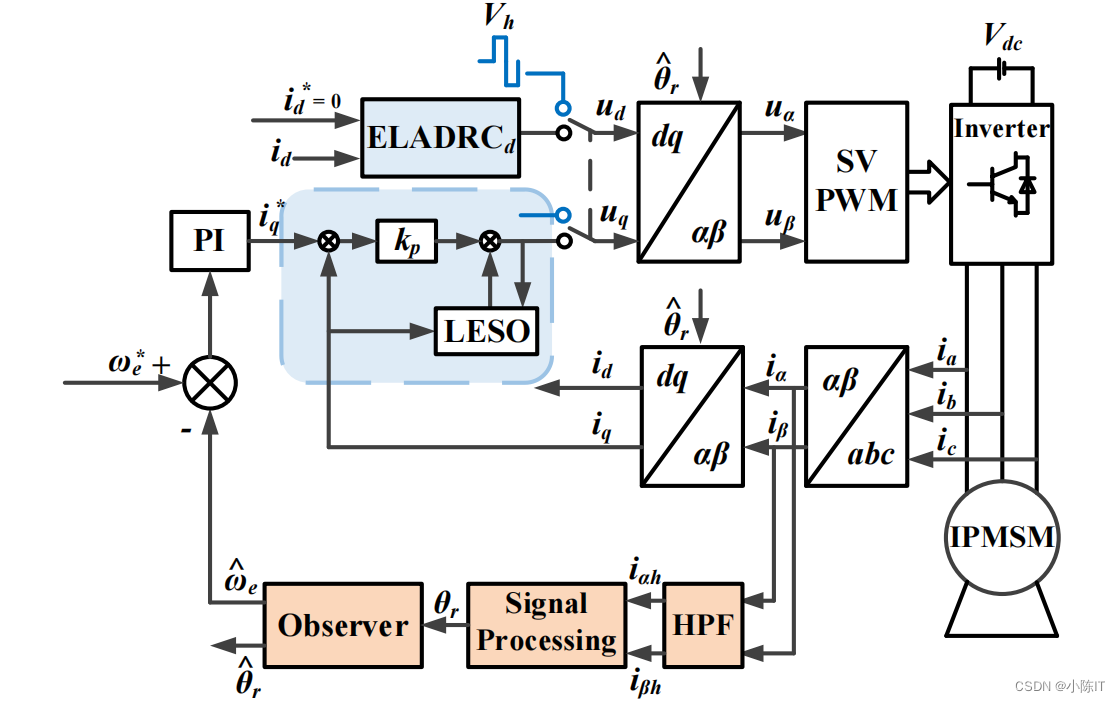
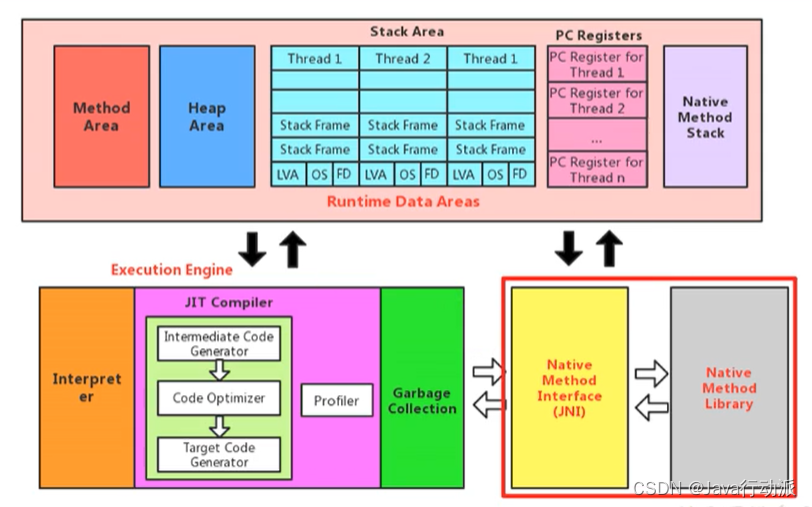
上面是文章的总控制框图,分成三个部分,第一个是ELADRC,代替电流环,第二个是信号提取,里面包含了Ldq的提取和θ的求解,第三个是观测器,用的是Luenberger observer
控制原理
ELADRC
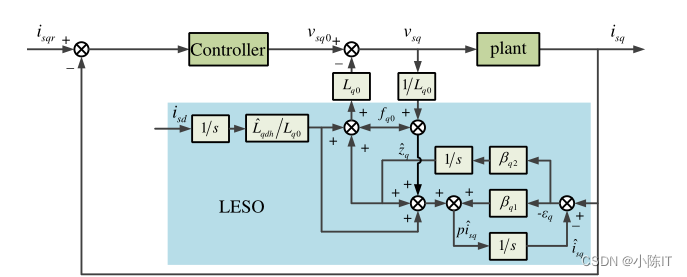
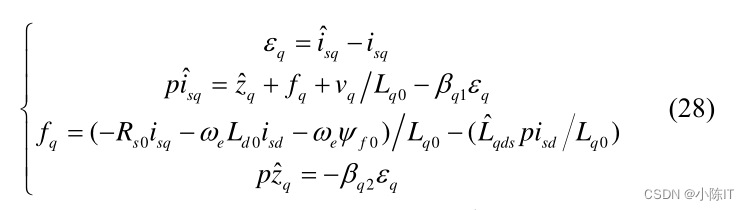

信号提取
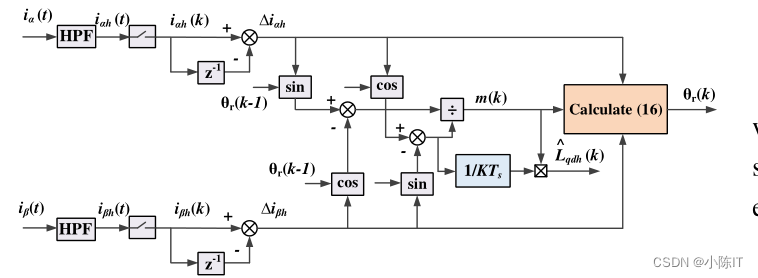
龙格贝尔观测器
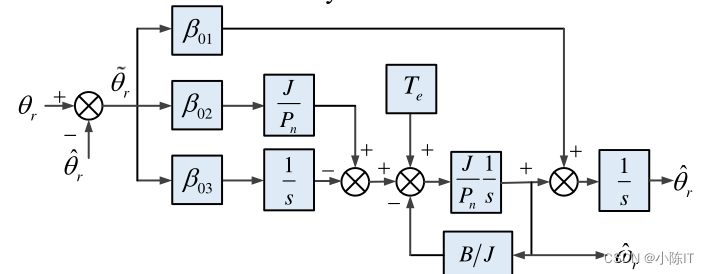
方波注入
注入的高频方波信号为:
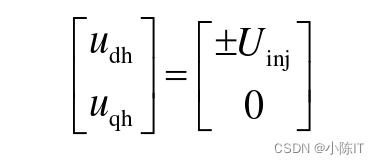
可以得到估计轴的高频响应电流为:
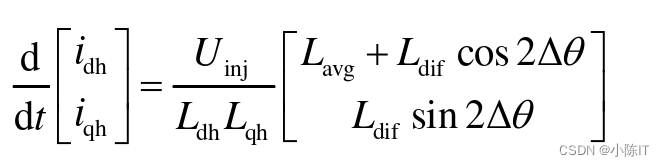
当向定子绕组注入高频电压信号时,所注入的高频信号频率远高于基波信号频率。因此,IPMSM 在a-β轴的电压模型可以表示为:
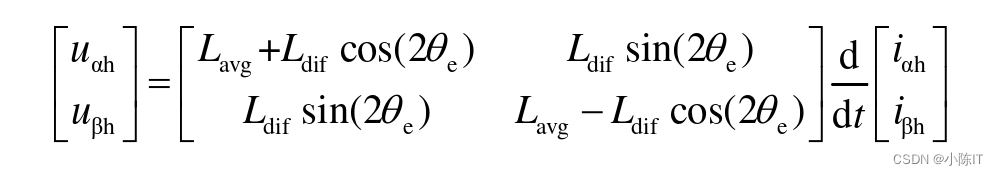
假定在一个采样周期内,电流线性变化,di/dt等于△i/△t,则可整理为:
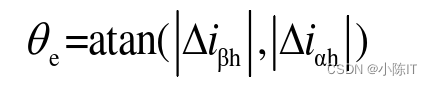
simulink仿真
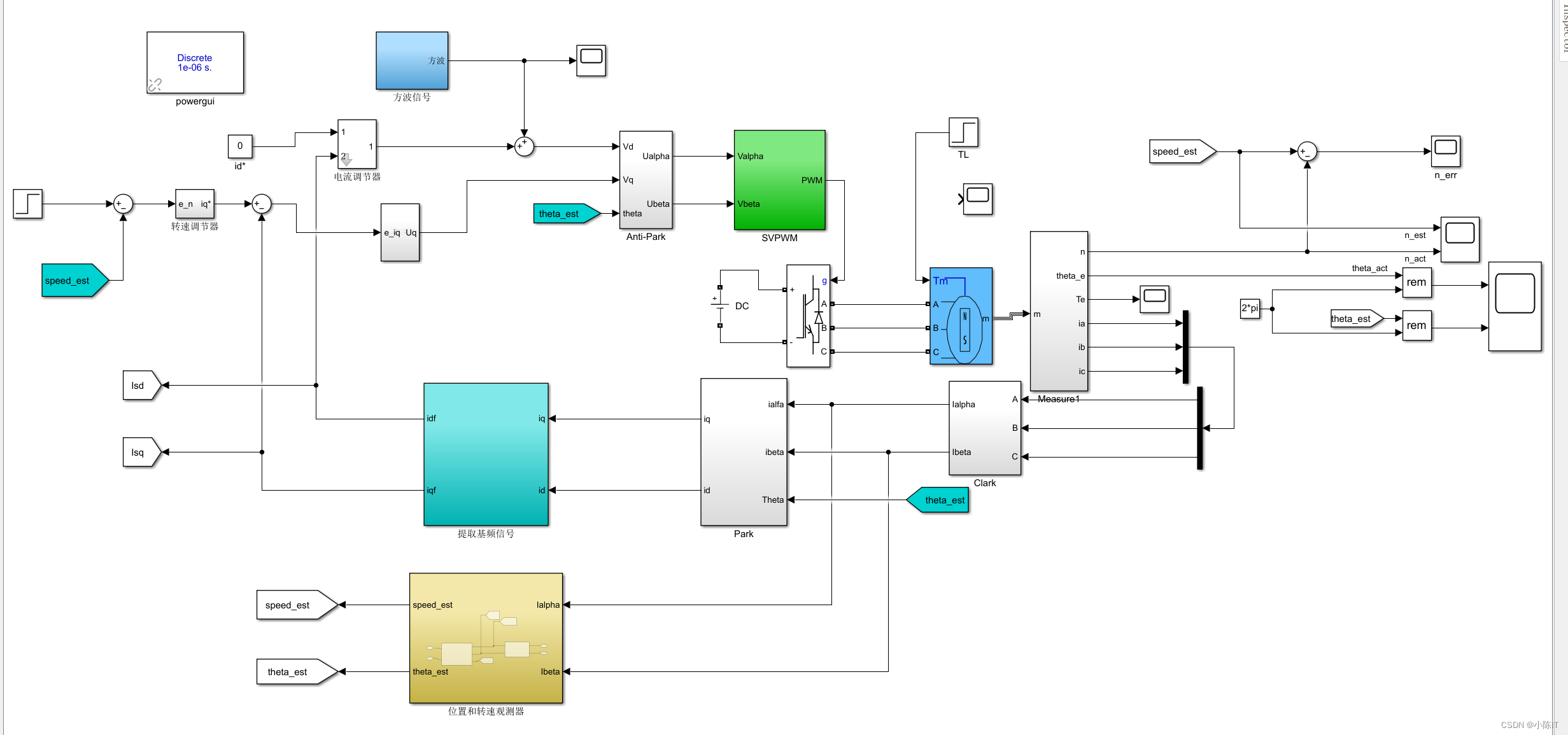
给定转速:
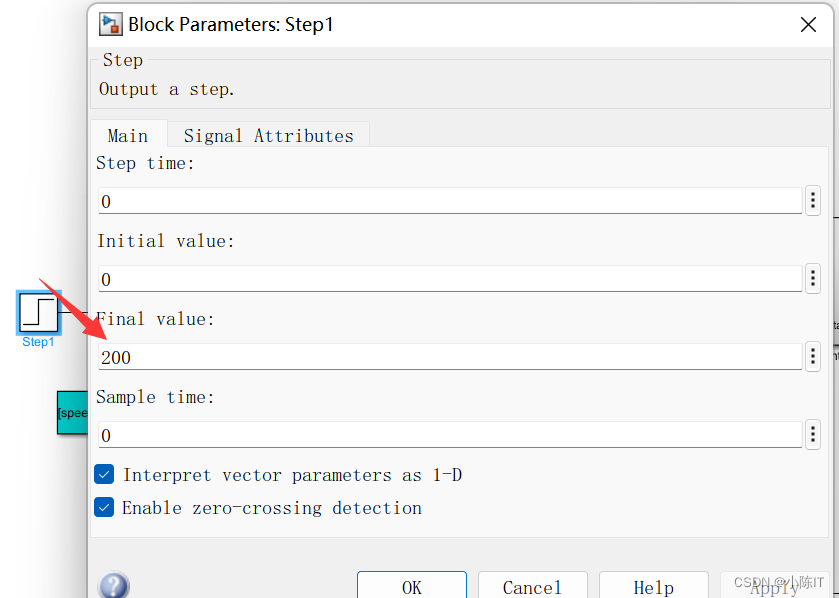
转速环:
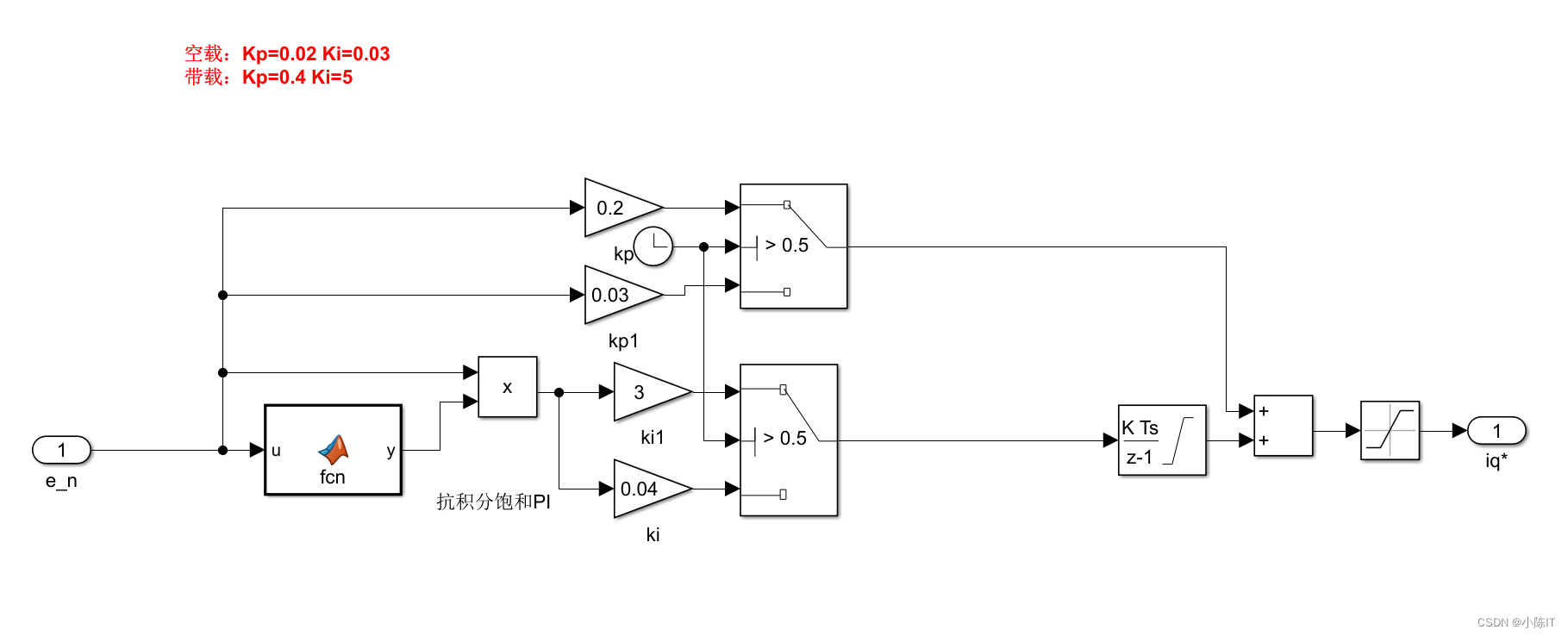
function y = fcn(u)
if (abs(u)>300)
y=0;
else
y=1;
end
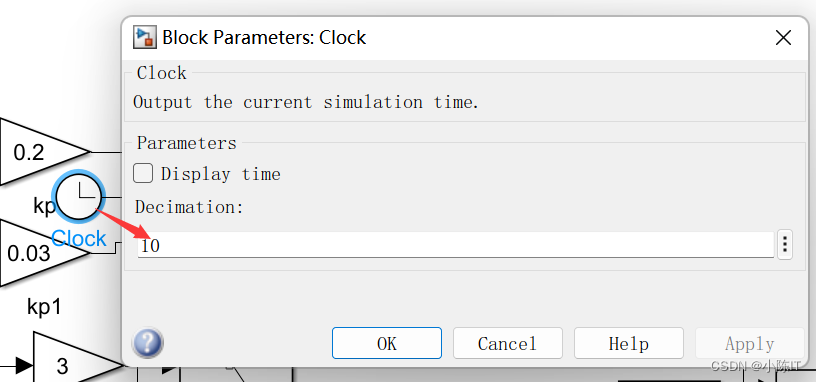
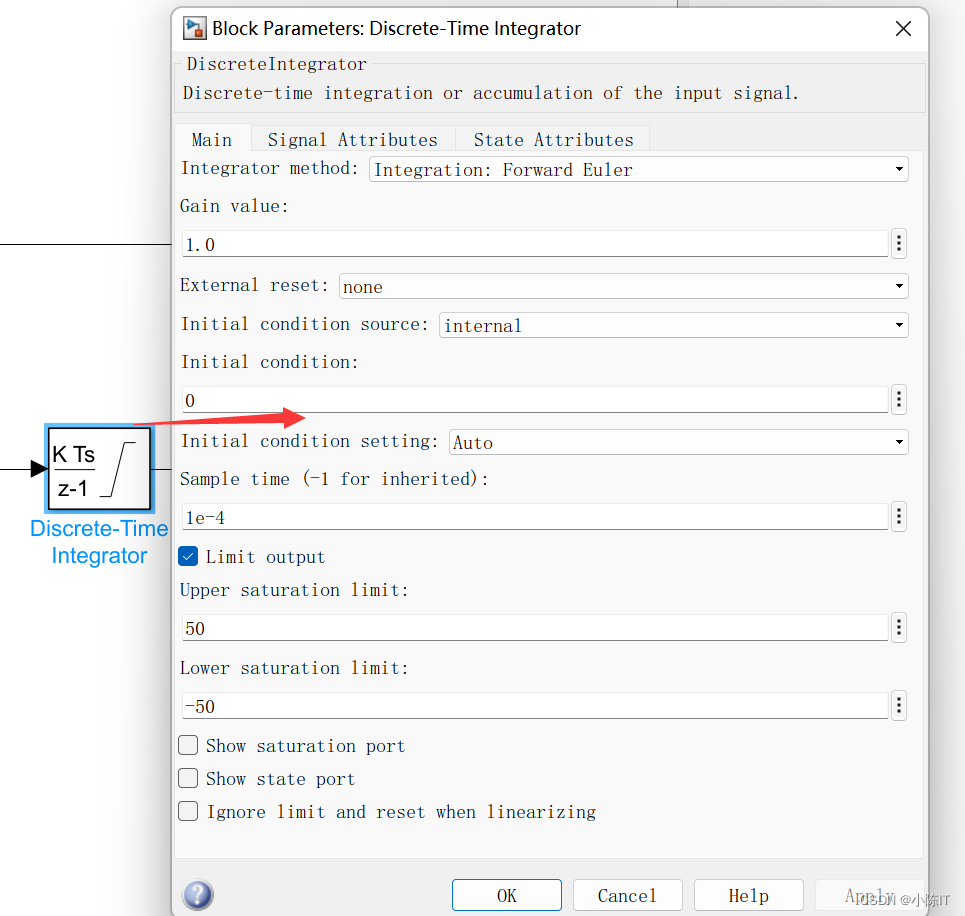
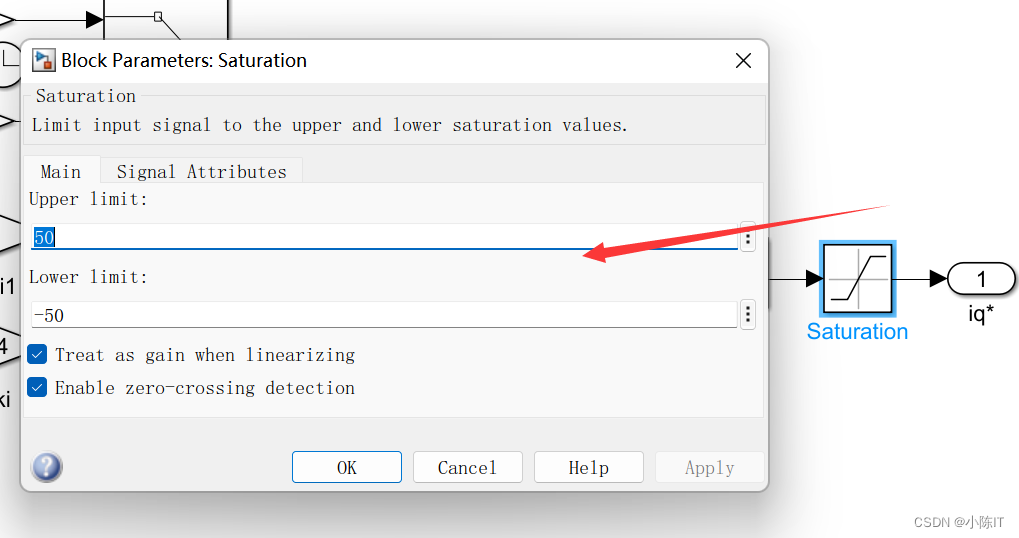
电流环:
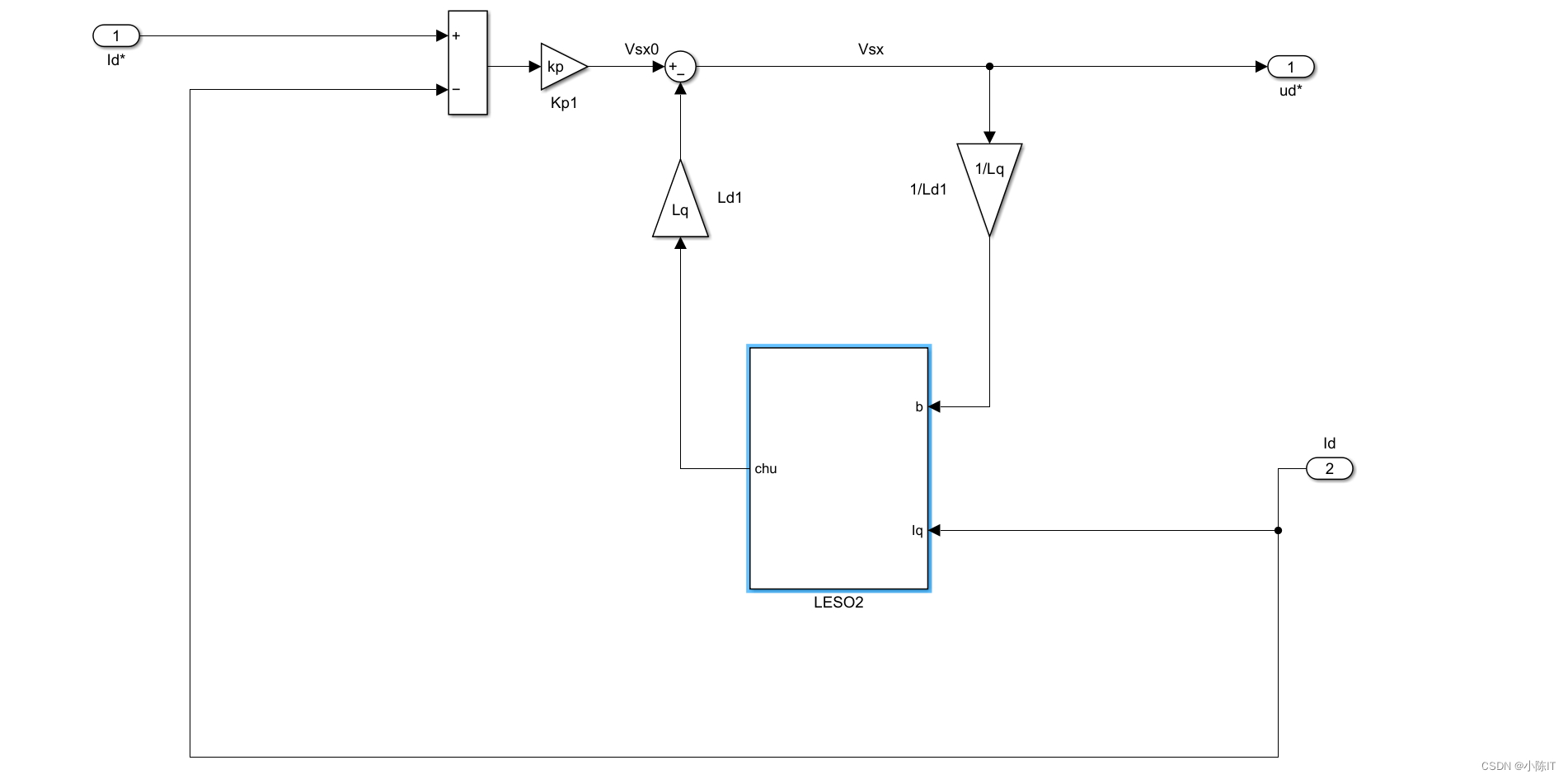
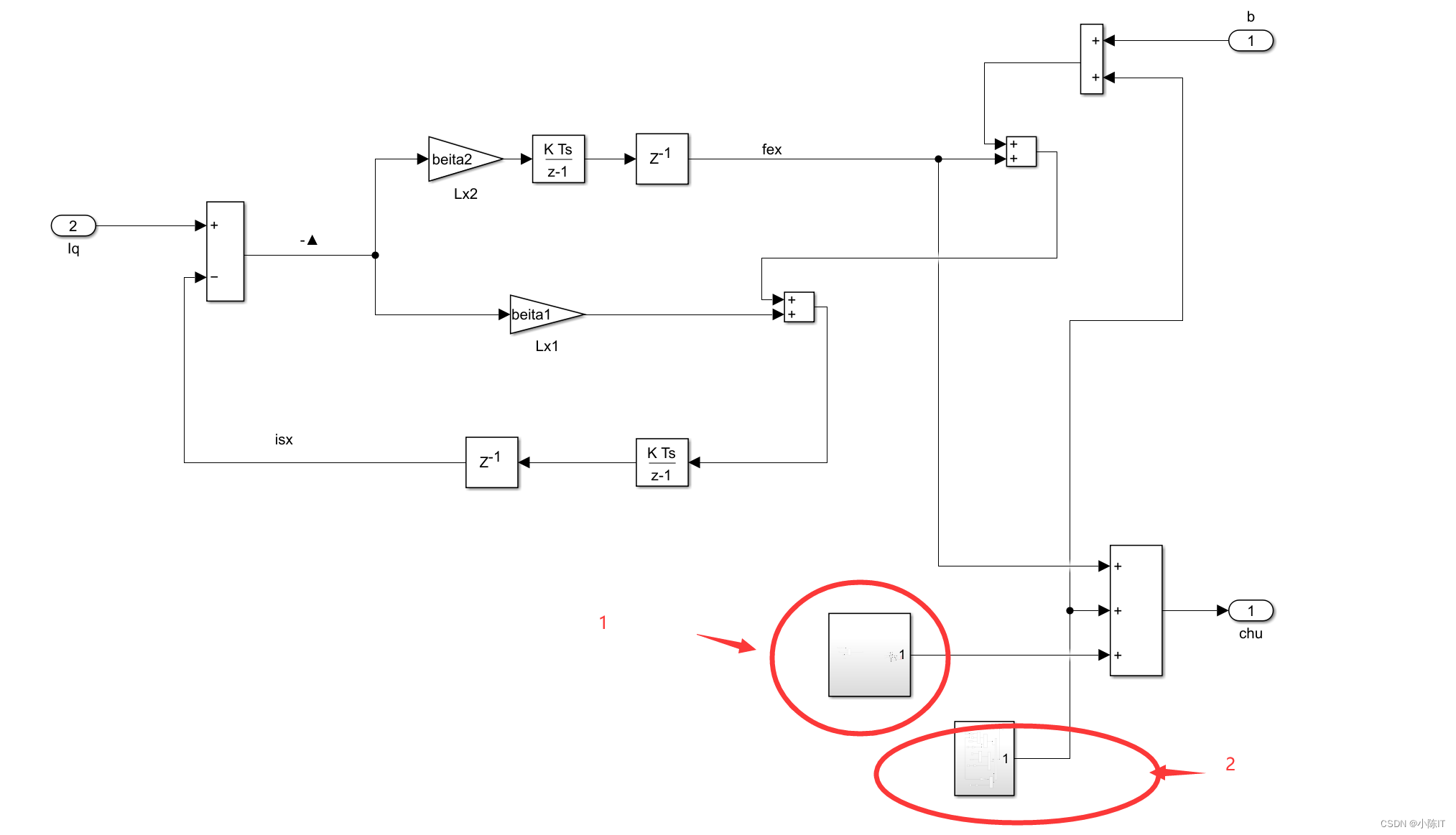
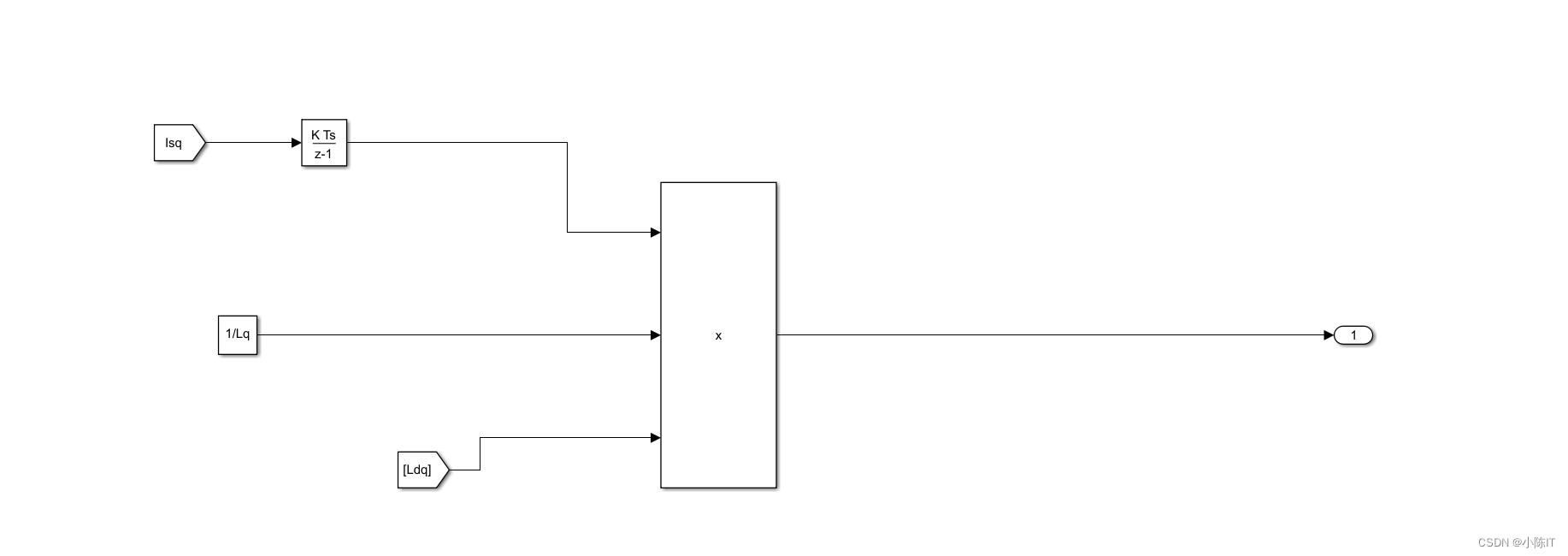
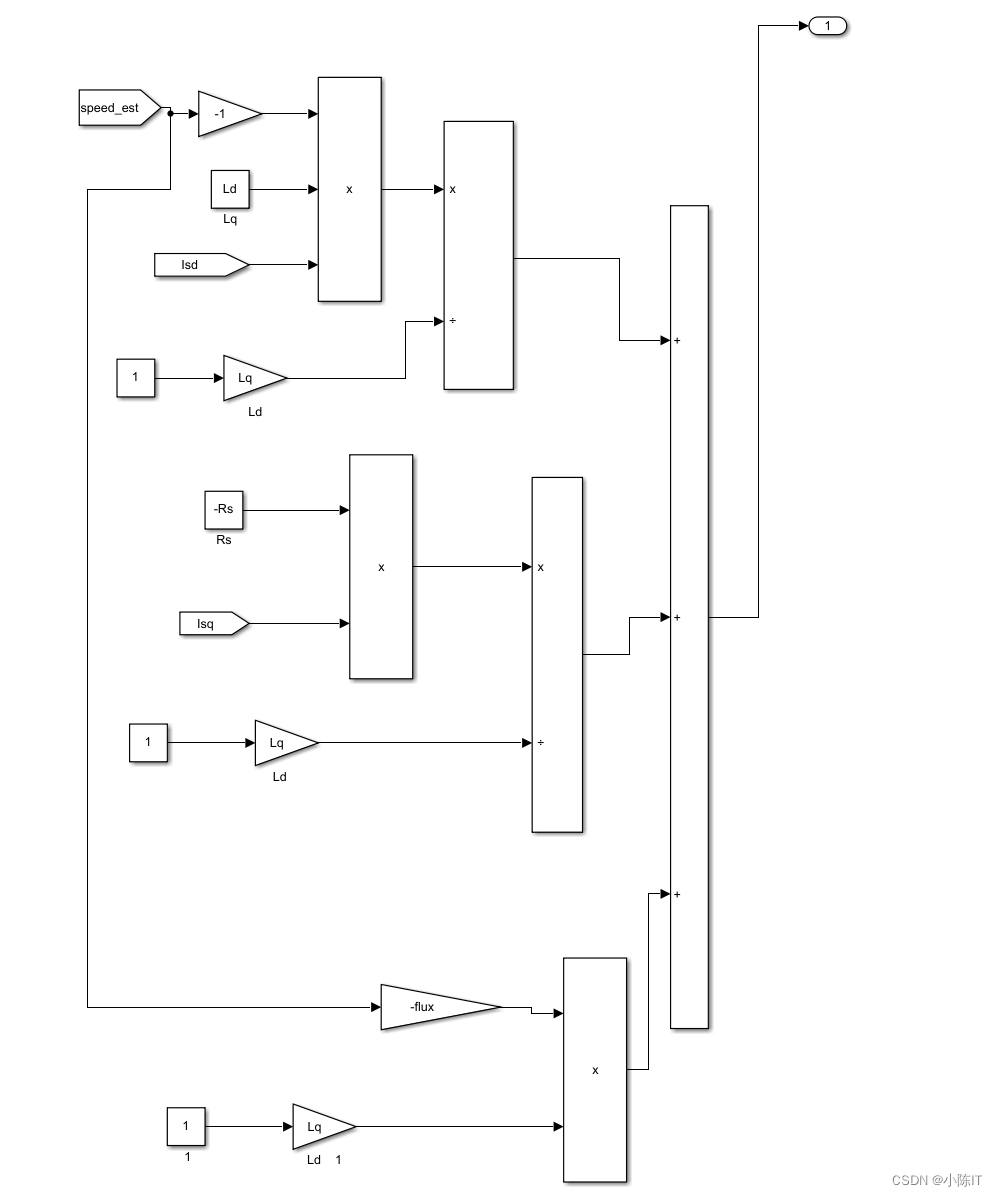
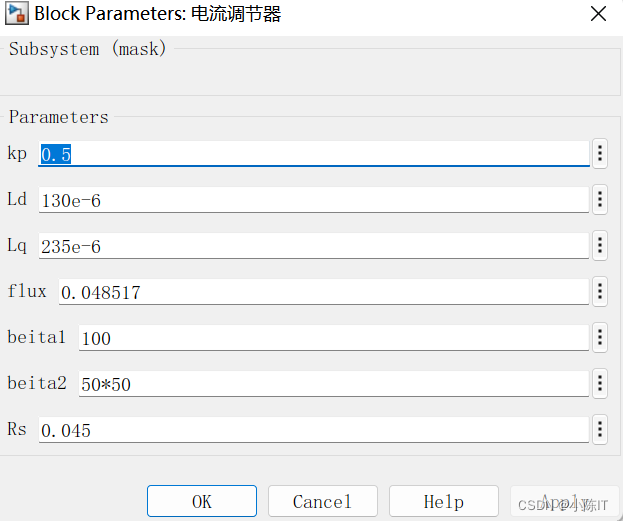
参数设置:
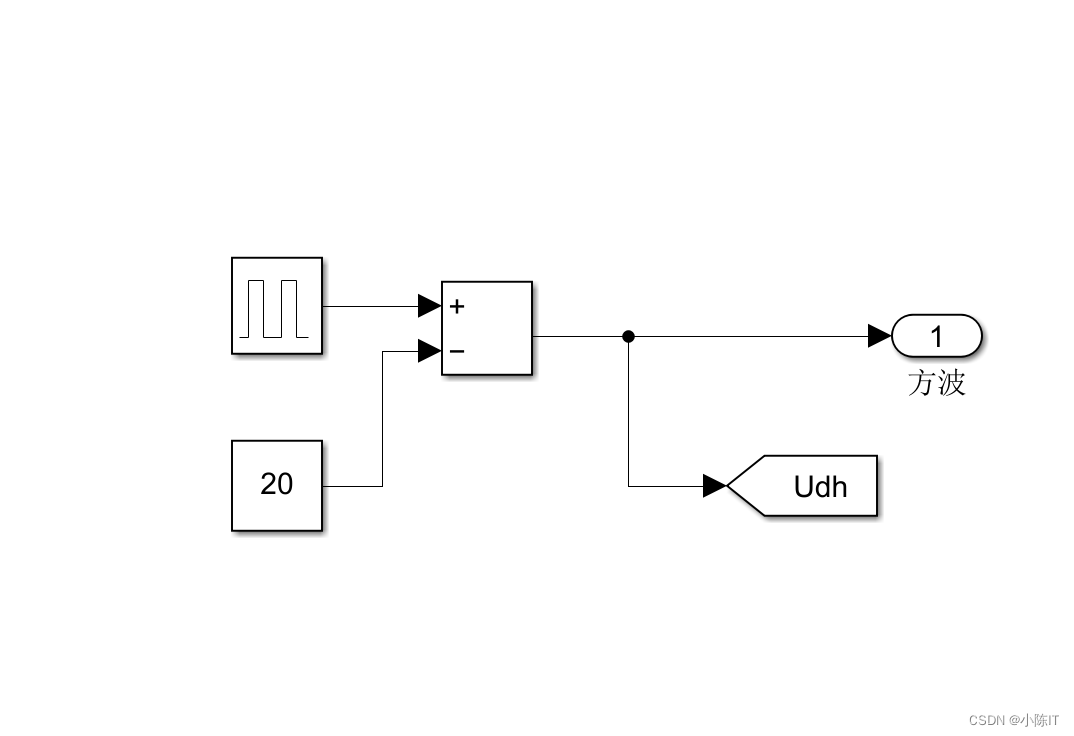
方波注入模块:
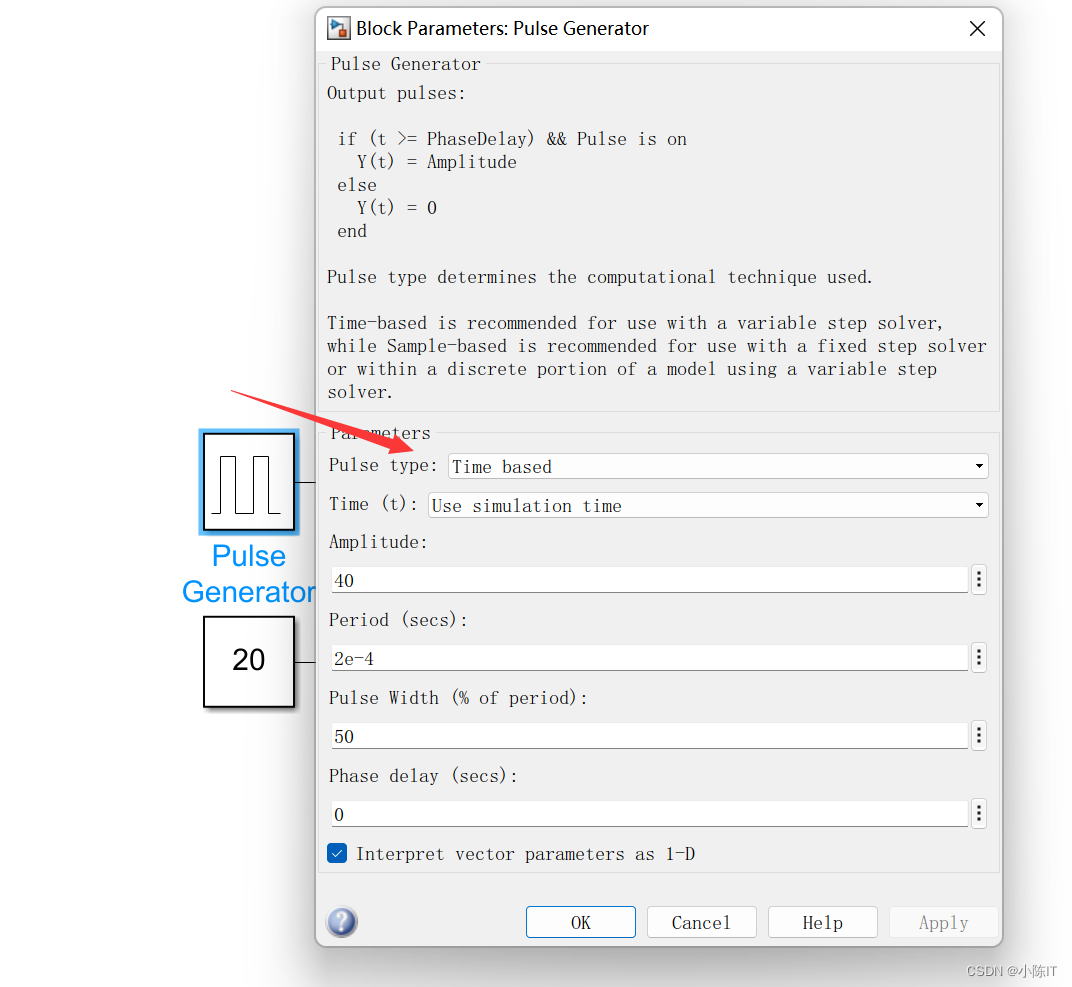
逆变器:
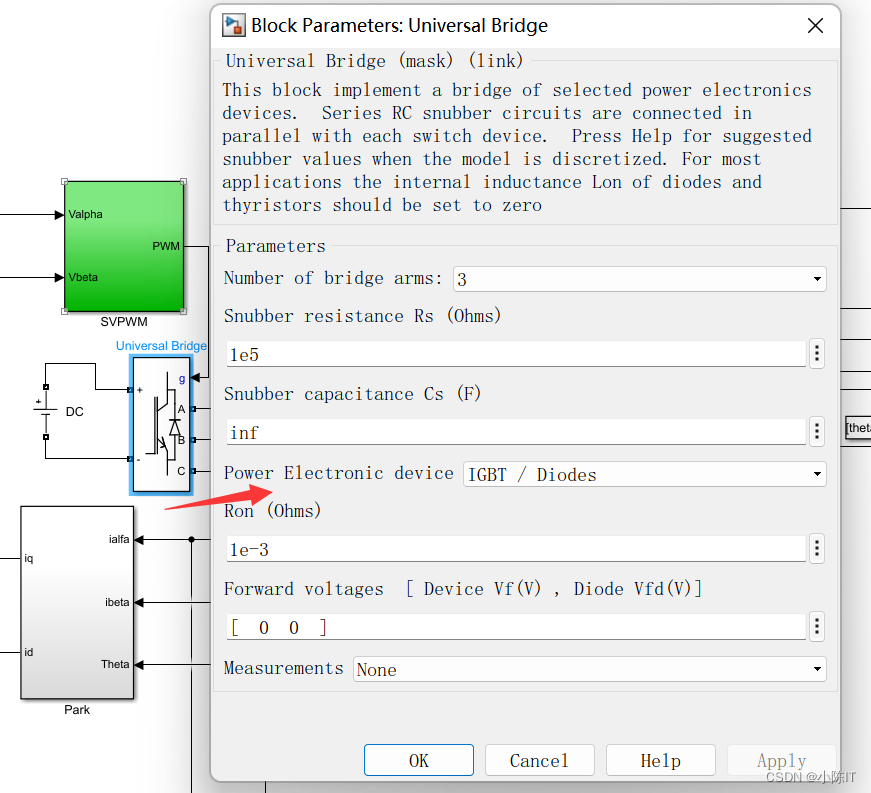
电机:
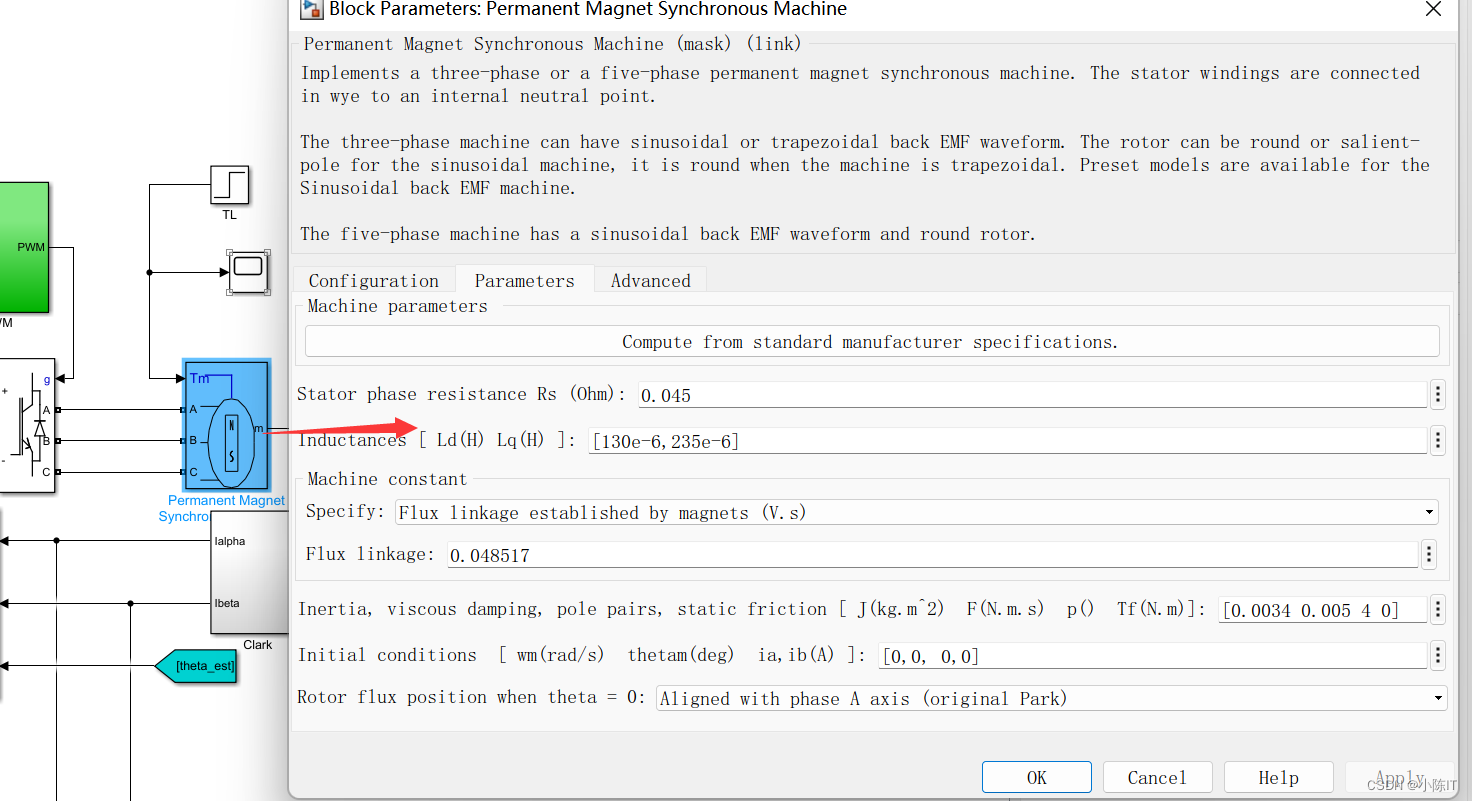
meaument模块:
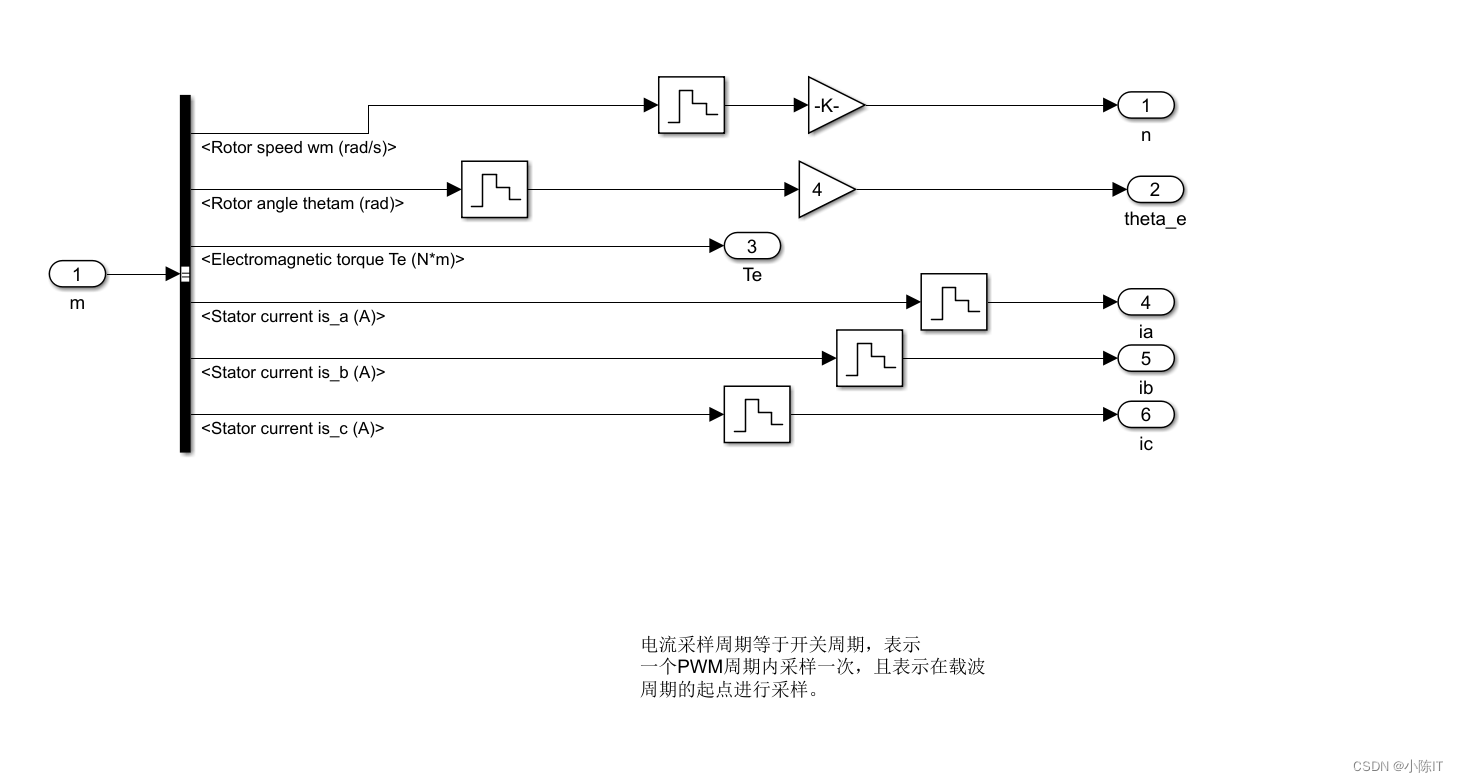
提取基频信号模型:
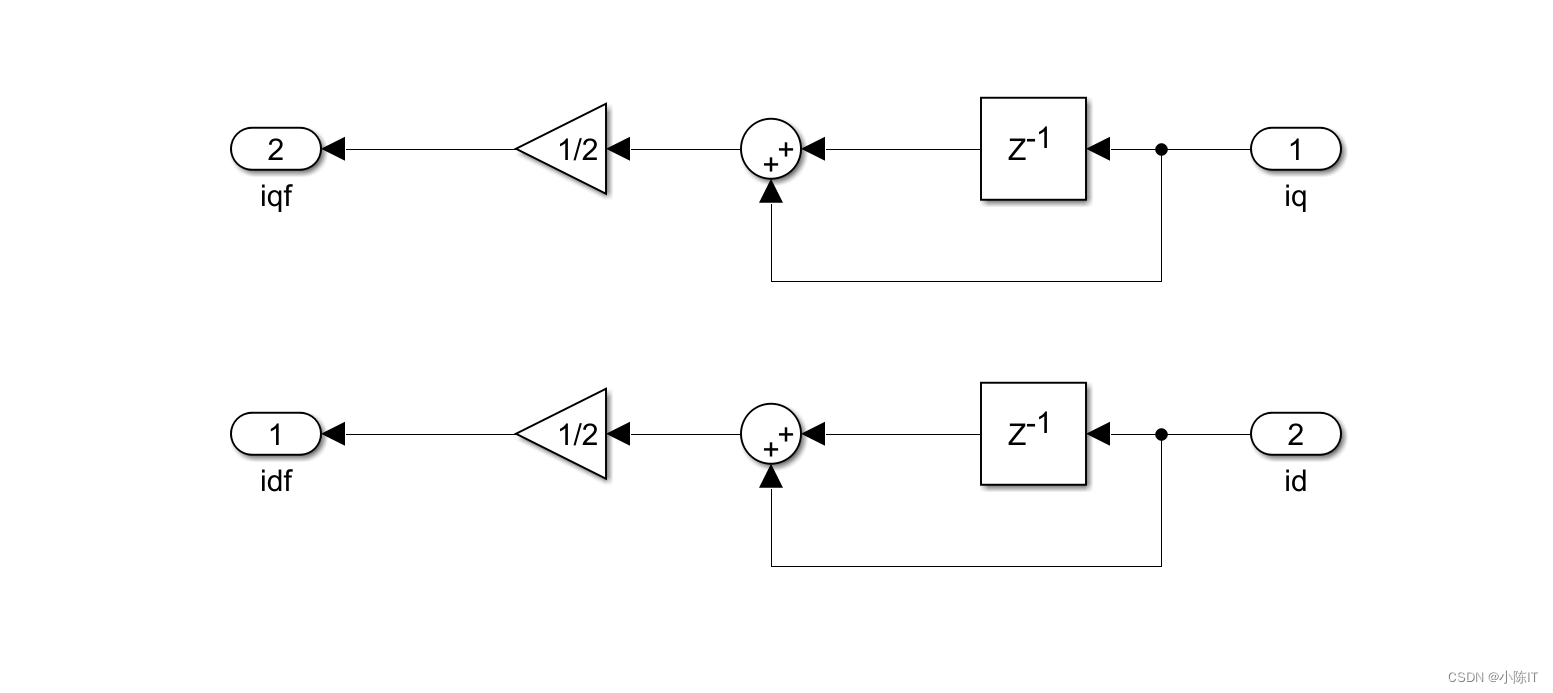
位置和转速观测器:
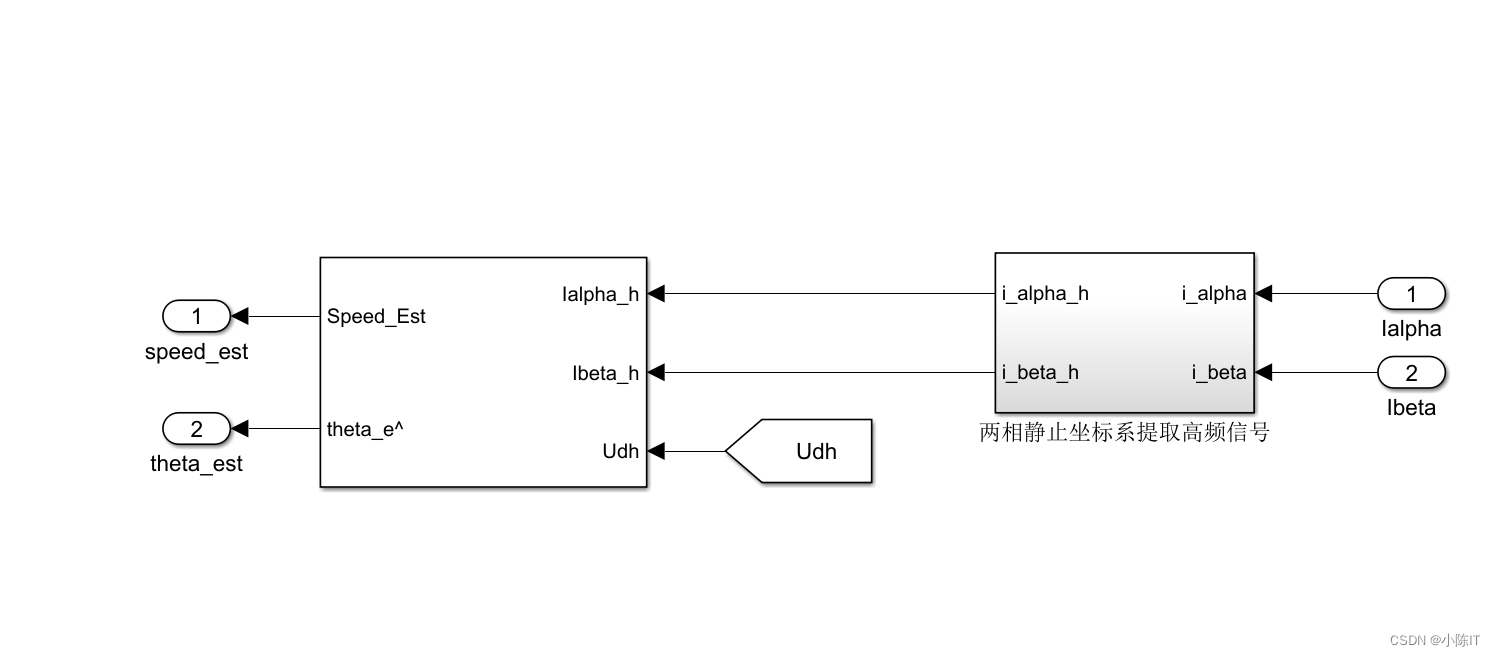
上面那个图的左边的模块:
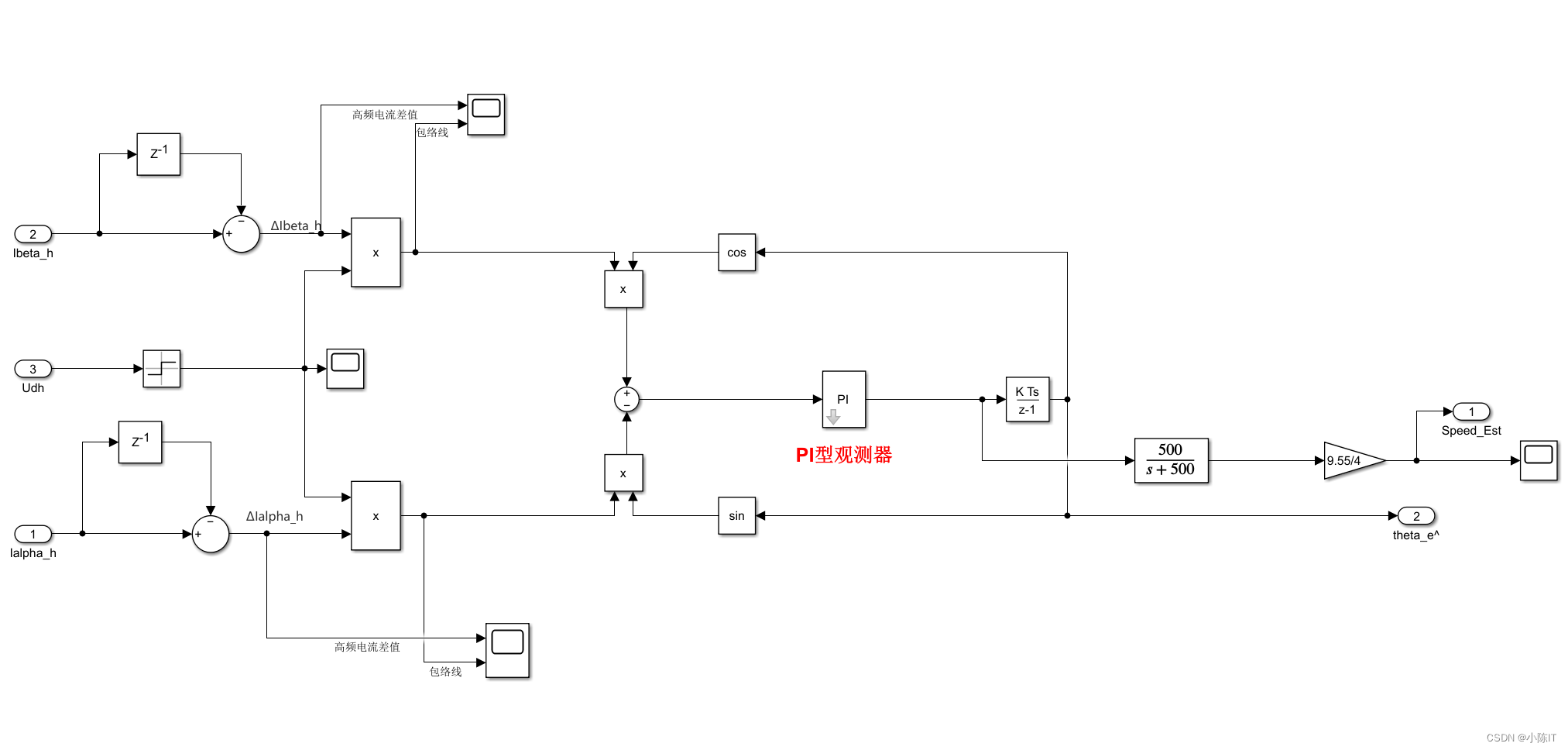
其中的PI:
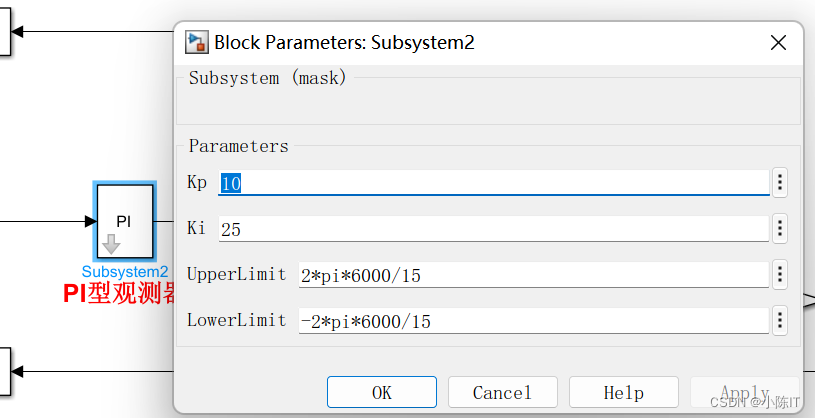
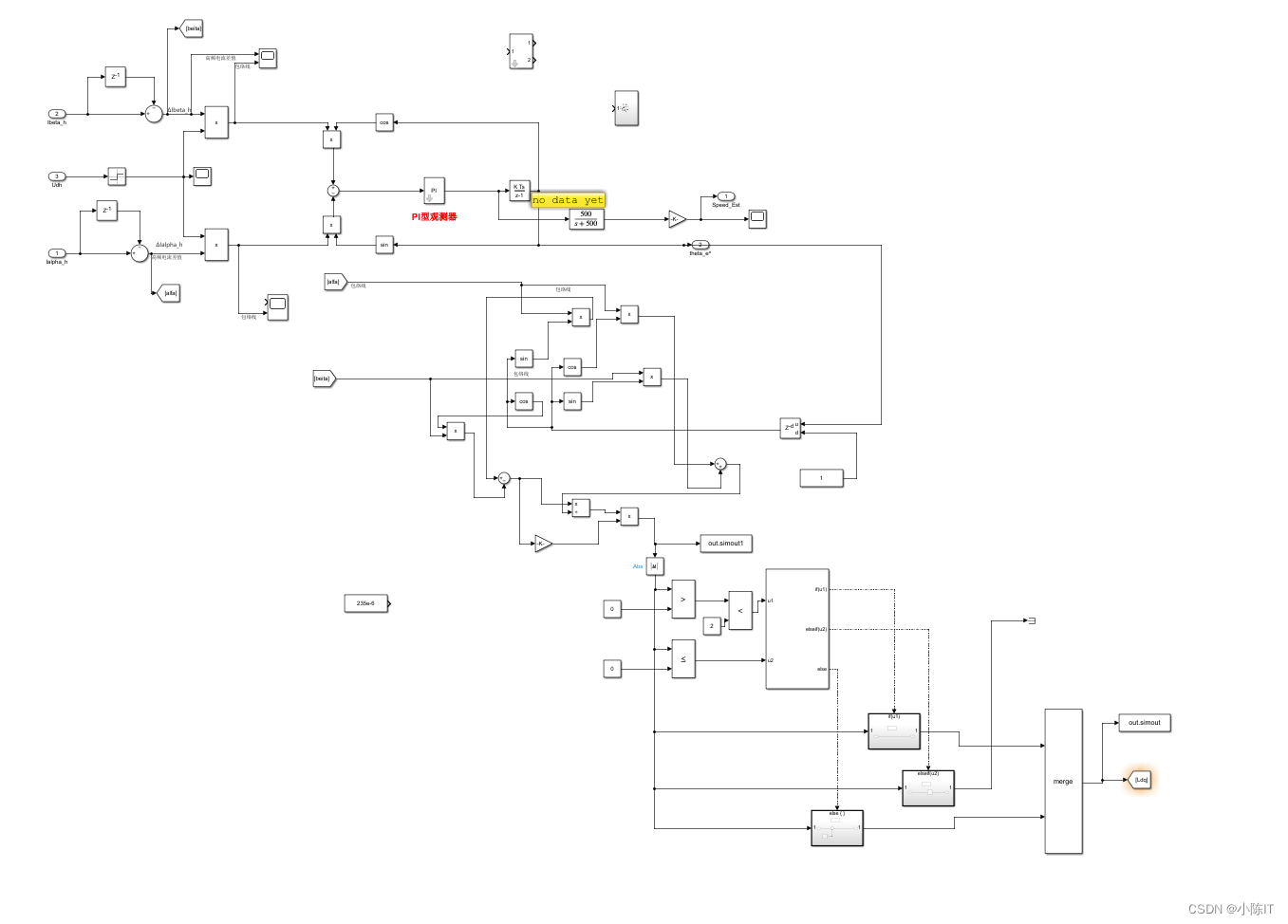
两相静止坐标系提取高频信号(右边模块):
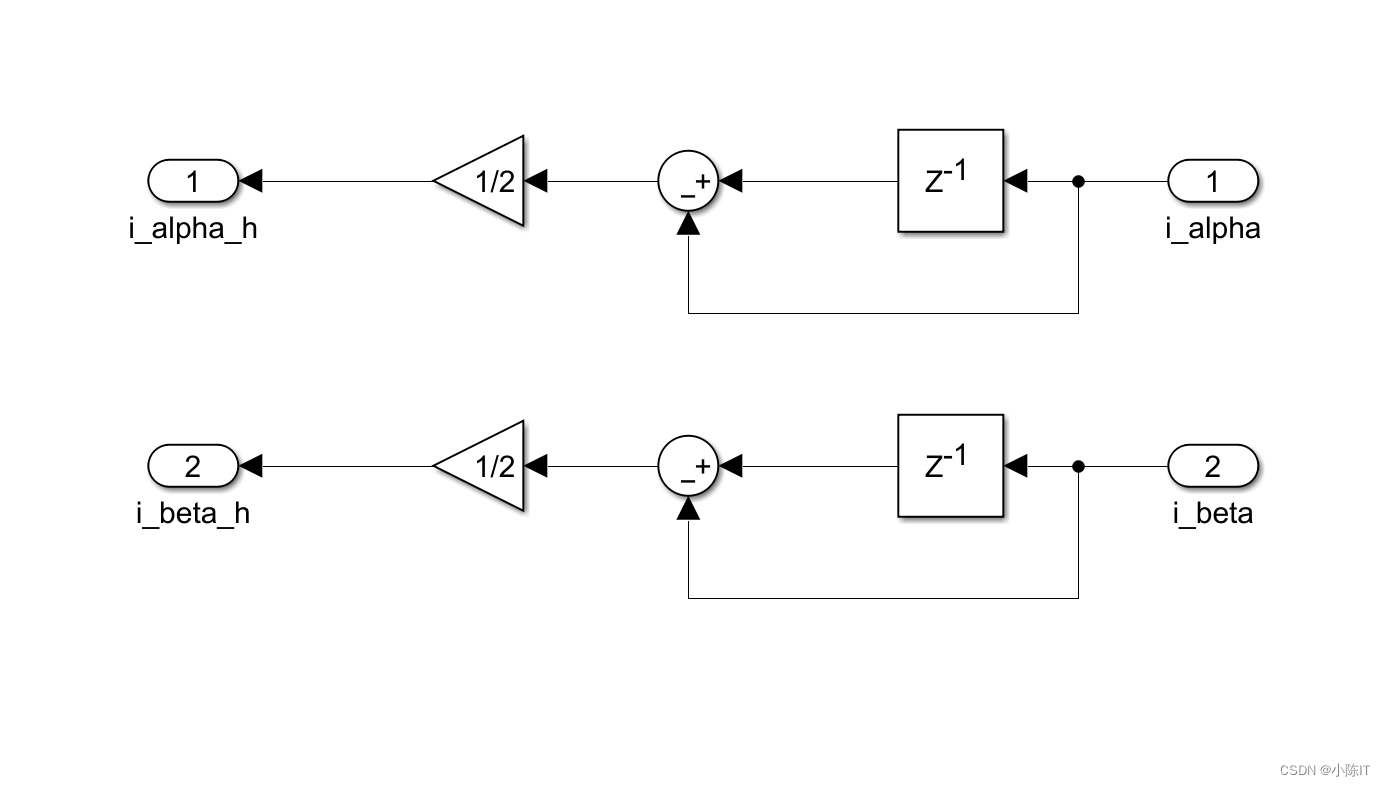
波形结果:
实际转速与估计转速波形:
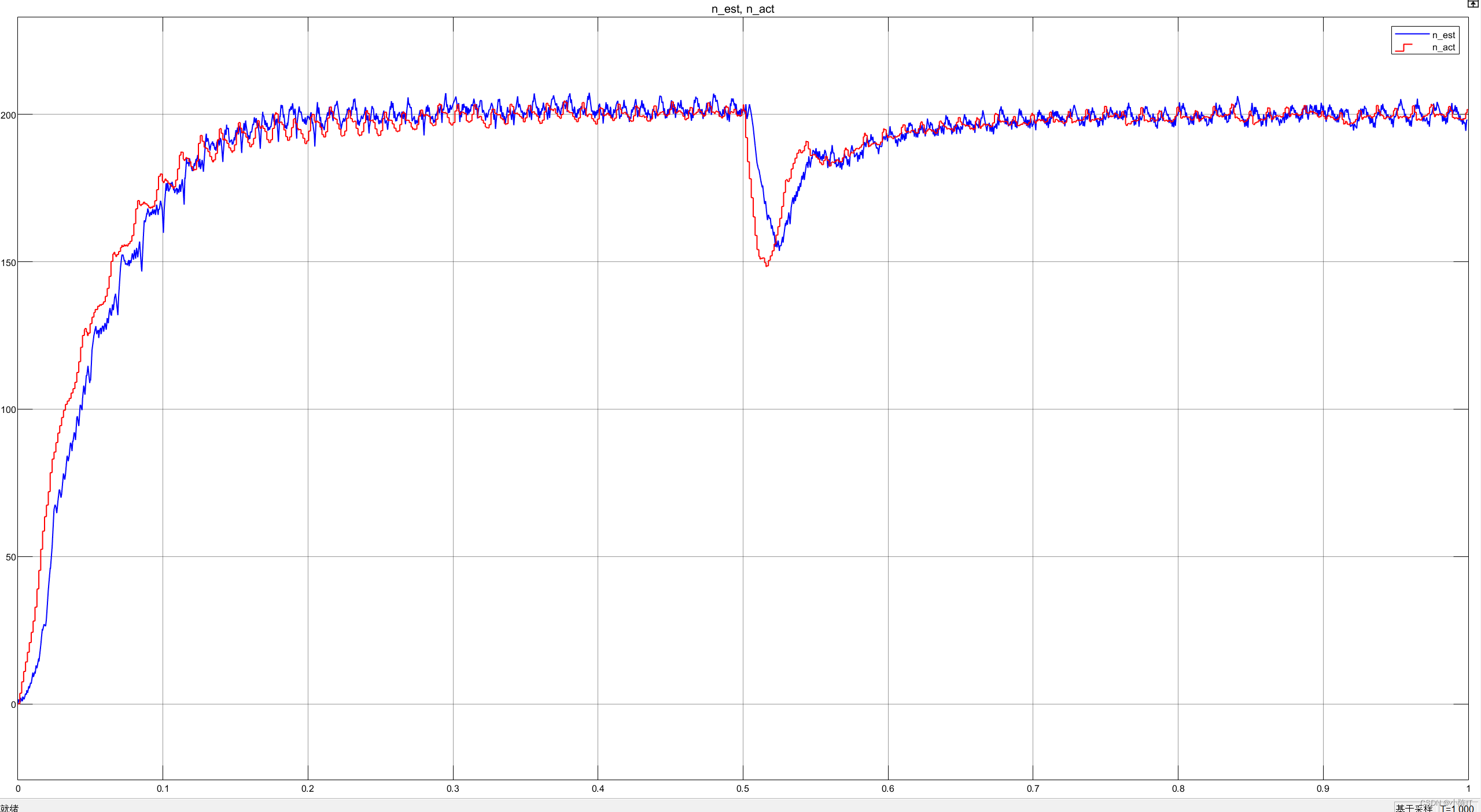
实际角度与估计角度波形:
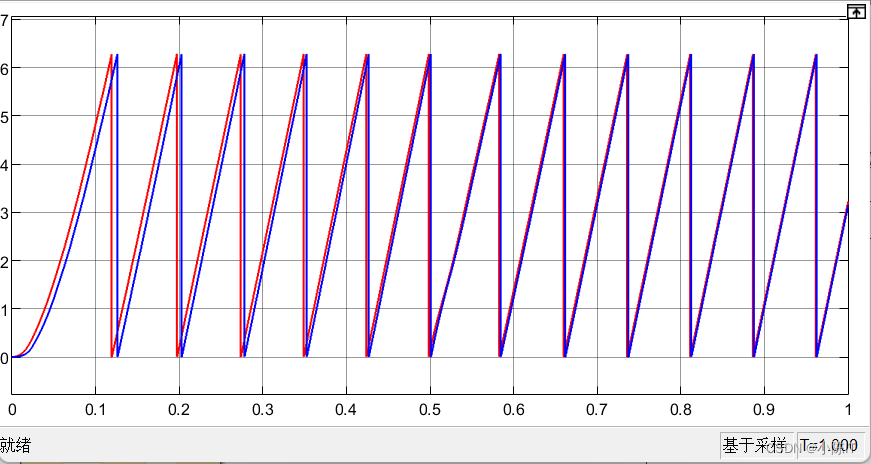
给个点赞和关注谢谢!!!!
还有就是模型参数已经给出,除了变换模块和SVPWM模块,你们用你们自己的模型试一下,不行再评论找我要,一般当天就会回复。