14天阅读挑战赛

本篇是学习了《趣学算法（第2版）》 第一章之后总结的。

上一篇讲到了等比数列求和问题，求$S_n=1+2+2^2+2^3+...+2^{63}=？$，该函数属于爆炸增量函数，如果采用常规运算，则要考虑算法的时间复杂度。

算法时间复杂度

常见的算法时间复杂度有以下几类。

1. 常数阶。
   常数阶算法的运行次数是一个常数，如5、20、100。常数阶算法的时间复杂度通常用O(1)表示。

2. 多项式阶。
   很多算法的时间复杂度是多项式，通常用 0(n)、$O(n^2)$、$0(n^3)$等表示。

3. 指数阶。
   指数阶算法的运行效率极差，程序员往往像躲“恶魔”一样避开这种算法。指数阶算法的时间复杂度通常用$O(2^n)$、$O(n!)$、$O(n^n)$等表示。

4. 对数阶。
   对数阶算法的运行效率较高，通常用$O(logn)$、$O(nlogn)$等表示。
   指数阶增量随着的增加而急剧增加，而对数阶增长缓慢。它们之间的关系如下：

$$O(1)＜O(logn)＜O(n)＜O(nlogn)＜O(n^2)＜O(n^3)＜O(2^n)O(n!)＜O(n^n)$$

在设计算法时，我们要注意算法复杂度增量的问题，尽量避免爆炸级增量。

算法知识点

• 斐波那契数

• 动态规划（拆分子问题；记住过往，减少重复计算）

算法题目

假设第1个月有1对初生的兔子，第2个月进入成熟期，第3个月开始生育兔子，而1对成熟的兔子每月会生
1对兔子，兔子永不死去……那么，由1对初生的兔子开始，12个月后会有多少对兔子呢？

做题思路

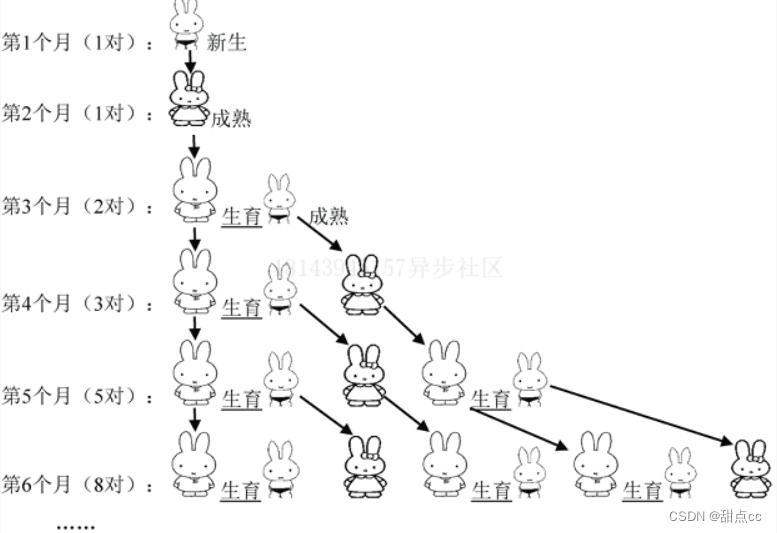
这个数列有如下十分明显的特点：从第3个月开始，$当月的兔子数=上月兔子数+当月新生兔子数$，而$当月新生兔子数=上上月的兔子数$。因此，前面相邻两项之和便构成后一项，换言之：
$$当月的兔子数=上月兔子数+上上月的兔子数$$

斐波那契数如下：

1 ，1 ，2 ，3 ，5 ，8， 13 ，21 ，34 ......

递归表达式

$$F(n)=\{\begin{array}{ll}1& ，\text{n=1}\\ 1& ，\text{n=2}\\ F(n-1)+F(n-2)& ，\text{n>2}\end{array}$$

根据递归表达式，初步的算法代码如下：

const fbn = (n) => {
  if (n == 1 || n == 2) {
		return 1
  } else {
		return fbn(n-2) + fbn(n-1)
	}
}

让我们看一下上面算法的时间复杂度，也就是计算的总次数$T(n)$

时间复杂度

时间复杂度算的是最坏情况下的时间复杂度

n=1时，T(n)=1
n=2时，T(n)=1；
n=3时，T(n)=3; //调用Fib1(2)和Fib1(1)并执行一次加法运算(Fib1(2)+Fib1(1))

当n>2时需要分别调用fbn(n-1)和fbn(n-2)，并执行一次加法运算，换言之：
$$n>2时，T(n)=T(n-1)+T(n-2)+1;$$

所以，$T(n)>=F(n)$

问题来了，怎么判断T(n)属于算法时间复杂度的哪种类型呢？

方法一：

画出递归树，每个节点表示计算一次

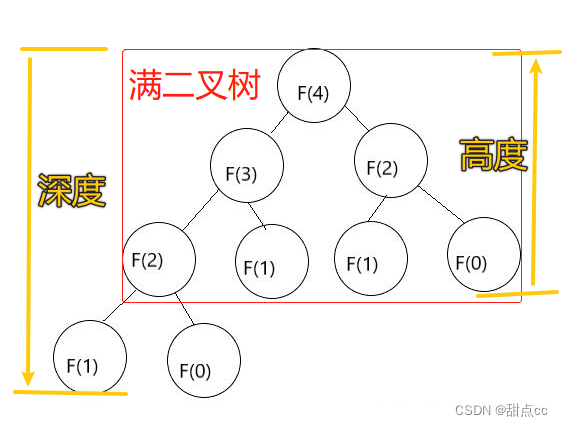
一棵满二叉树，节点总数就和树的高度呈指数关系

递归树 F(n)里面存在满二叉树，所以时间复杂度是指数阶的。

方法二：

使用公式进行递推

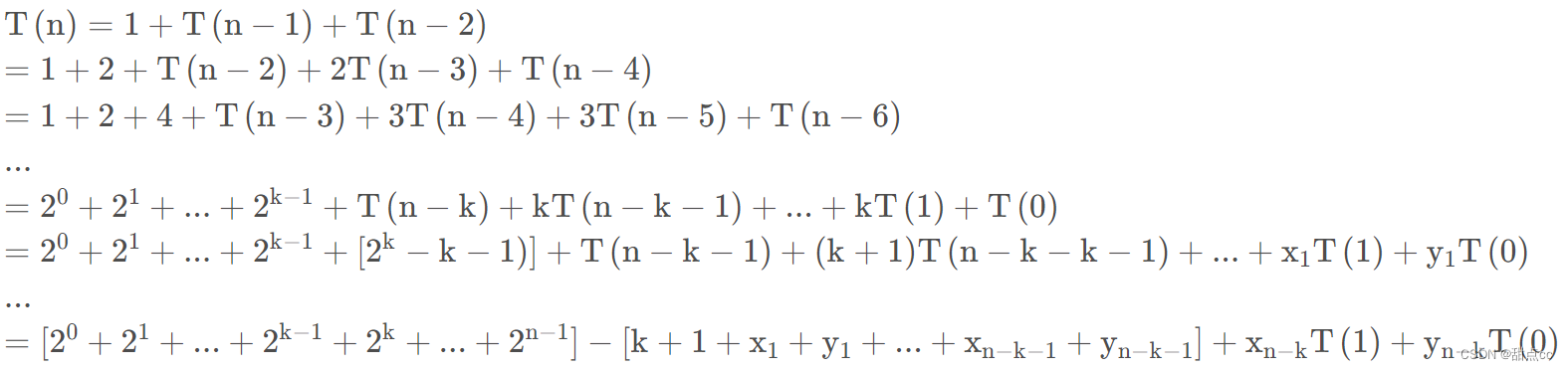
因为时间复杂度算的是最坏情况下的时间复杂度，所以计算第一个括号内的即可

即：$T(n)=O(2^n)$，时间复杂度是指数阶的

算法改进

降低时间复杂度

不难发现：上面基于递归表达式的算法，存在大量的重复计算，增大了算法的时间复杂度，所以我们可以做出如下改进，以减少时间复杂度

// 利用数组记录过往的值，直接使用，避免重复计算
const fbn2 = (n) => {
  let arr = new Array(n + 1); // 定义 n + 1 长度的数组
  arr[1] = 1;
  arr[2] = 1;
  for (let i = 3; i <= n; i++) {
    arr[i] = arr[i - 1] + arr[i - 2]
  }
  return arr[n]
}

很显然上面算法的时间复杂度是$O(n)$，时间复杂度从指数阶降到了多项式阶。

由于上面算法使用数组记录了所有项的值，所以，算法的空间复杂度变成了$O(n)$，我们可以继续改进算法，来降低算法的空间复杂度

降低空间复杂度

采用临时变量，来迭代记录上一步计算出来的值，代码如下：

const fbn3 = (n) => {
  if (n === 1 || n === 2) {
    return 1;
  }
  let pre1 = 1 // pre1，pre2记录前面两项
  let pre2 = 1
  let tmp = ''

  for (let i = 3; i <= n; i++) {
    tmp = pre1 + pre2 // 2
    pre1 = pre2 // 1
    pre2 = tmp // 2
  }
  return pre2
}

使用了三个辅助变量，时间复杂度还是$O(n)$，空间复杂度降为$O(1)$

测试算法计算时间

// 斐波那契数列
// 1 ，1 ，2 ，3 ，5 ，8， 13 ，21 ，34 ......

const fbn = (n) => {
  if (n == 1 || n == 2) {
		return 1
  } else {
		return fbn(n-2) + fbn(n-1)
	}
}
console.time('fbn')
console.log('fbn(40)=', fbn(40))
console.timeEnd('fbn')

// 利用数组记录过往的值，直接使用，避免重复计算
const fbn2 = (n) => {
  let arr = new Array(n + 1); // 定义 n + 1 长度的数组
  arr[1] = 1;
  arr[2] = 1;
  for (let i = 3; i <= n; i++) {
    arr[i] = arr[i - 1] + arr[i - 2]
  }
  return arr[n]
}

console.time('fbn2')
console.log('fbn2(40)=', fbn2(40))
console.timeEnd('fbn2')

const fbn3 = (n) => {
  if (n === 1 || n === 2) {
    return 1;
  }
  let pre1 = 1 // pre1，pre2记录前面两项
  let pre2 = 1
  let tmp = ''

  for (let i = 3; i <= n; i++) {
    tmp = pre1 + pre2 // 2
    pre1 = pre2 // 1
    pre2 = tmp // 2
  }
  return pre2
}

console.time('fbn3')
console.log('fbn3(40)=', fbn3(40))
console.timeEnd('fbn3')

测试结果如下：

fbn(40)= 102334155
fbn: 667.76ms
fbn2(40)= 102334155
fbn2: 0.105ms
fbn3(40)= 102334155
fbn3: 0.072ms

小结

能不能继续降阶，使算法的时间复杂度更低呢？
实质上，斐波那契数列的时间复杂度还可以降到对数阶$O(logn)$，好厉害!!!后面继续探索吧

---

我是 甜点cc

热爱前端，也喜欢专研各种跟本职工作关系不大的技术，技术、产品兴趣广泛且浓厚，等待着一个创业机会。本号主要致力于分享个人经验总结，希望可以给一小部分人一些微小帮助。

希望能和大家一起努力营造一个良好的学习氛围，为了个人和家庭、为了我国的互联网物联网技术、数字化转型、数字经济发展做一点点贡献。数风流人物还看中国、看今朝、看你我。