DS期末复习卷（九）

news2024/9/30 19:32:30

一、选择题(30分)

1．下列程序段的时间复杂度为（A ）。
for(i=0； i<m； i++) for(j=0； j<t； j++) c[i][j]=0；
for(i=0； i<m； i++) for(j=0； j<t； j++) for(k=0； k<n； k++) c[i][j]=c[i][j]+a[i][k]*b[k][j]；
(A) O(m * n * t) (B) O(m+n+t) ( C) O(m+n * t) (D) O(m * t+n)

2．设顺序线性表中有n个数据元素，则删除表中第i个元素需要移动（ A ）个元素。
(A) n-i (B) n+l -i ( C) n-1-i (D) i

3．设F是由T1、T2和T3三棵树组成的森林，与F对应的二叉树为B，T1、T2和T3的结点数分别为N1、N2和N3，则二叉树B的根结点的左子树的结点数为（A ）。
(A) N1-1 (B) N2-1 (C ) N2+N3 (D) N1+N3

(1)T1,T2,T3先分别转化为二叉树，除掉根结点，其它结点都转化为根结点的左孩子
(2)第一棵二叉树不动，后面的二叉树分别是前面二叉树的右孩子。
故本题中T1不动，左孩子结点N1-1

4．利用直接插入排序法的思想建立一个有序线性表的时间复杂度为（ C ）。
(A) O(n) (B) O(nlog2n) ( C) O(n^2) (D) O(1og2n)

直接插入排序算法的时间复杂度为O（n^2）

5．设指针变量p指向双向链表中结点A，指针变量s指向被插入的结点X，则在结点A的后面插入结点X的操作序列为（ D ）。
(A) p->right=s； s->left=p； p->right->left=s； s->right=p->right；
(B) s->left=p；s->right=p->right；p->right=s； p->right->left=s；
© p->right=s； p->right->left=s； s->left=p； s->right=p->right；
(D) s->left=p；s->right=p->right；p->right->left=s； p->right=s；

6．下列各种排序算法中平均时间复杂度为O(n2)是（ D ）。
(A) 快速排序 (B) 堆排序 ( C) 归并排序 (D) 冒泡排序

时间复杂度为n^2的排序算法有直接插入排序、冒泡排序

7．设输入序列1、2、3、…、n经过栈作用后，输出序列中的第一个元素是n，则输出序列中的第i个输出元素是（ C ）。
(A) n-i (B) n-1-i ( C) n+l -i (D) 不能确定

8．设散列表中有m个存储单元，散列函数H(key)= key % p，则p最好选择（ B ）。
(A) 小于等于m的最大奇数 (B) 小于等于m的最大素数
(C ) 小于等于m的最大偶数 (D) 小于等于m的最大合数

减少冲突

9．设在一棵度数为3的树中，度数为3的结点数有2个，度数为2的结点数有1个，度数为1的结点数有2个，那么度数为0的结点数有（ C ）个。
(A) 4 (B) 5 ( C) 6 (D) 7

n0=1+n2+2n3=1+1+4=6

10.设完全无向图中有n个顶点，则该完全无向图中有（ A ）条边。
(A) n(n-1)/2 (B) n(n-1) ( C) n(n+1)/2 (D) (n-1)/2

无向图n(n-1)/2
有向图n(n-1)

11.设顺序表的长度为n，则顺序查找的平均比较次数为（ C ）。
(A) n (B) n/2 (C ) (n+1)/2 (D) (n-1)/2

最小是1 最大是n

12.设有序表中的元素为(13，18，24，35，47，50，62)，则在其中利用二分法查找值为24的元素需要经过（ C ）次比较。
(A) 1 (B) 2 ( C) 3 (D) 4

35 18 26

13.设顺序线性表的长度为30，分成5块，每块6个元素，如果采用分块查找，则其平均查找长度为（ D ）。
(A) 6 (B) 11 ( C) 5 (D) 6.5

找块：（1+2+3+4+5）/5=3
在块内找元素： (1+2+3+4+5+6)/6=3.5
合计：3+3.5=6.5

14.设有向无环图G中的有向边集合E={<1，2>，<2，3>，< 3，4>，<1，4>}，则下列属于该有向图G的一种拓扑排序序列的是（A ）。
(A) 1，2，3，4 (B) 2，3，4，1 ( C) 1，4，2，3 (D) 1，2，4，3

“拓扑排序对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边<u,v>∈E(G)，则u在线性序列中出现在v之前。

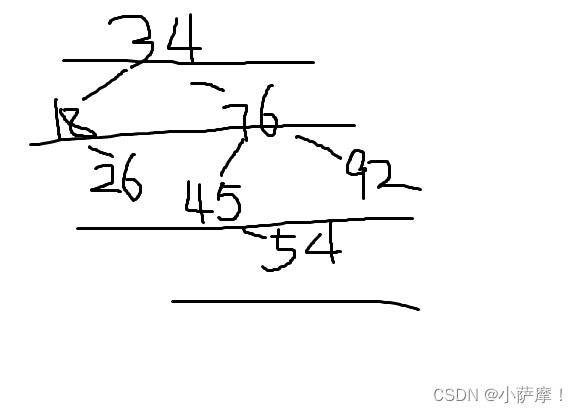
15.设有一组初始记录关键字序列为(34，76，45，18，26，54，92)，则由这组记录关键字生成的二叉排序树的深度为（ A ）。
(A) 4 (B) 5 ( C) 6 (D) 7

这里是引用

二、填空题(30分)

1． 设指针p指向单链表中结点A，指针s指向被插入的结点X，则在结点A的前面插入结点X时的操作序列为：

  1. s->next=___________；2) p->next=s；3) t=p->data；

  2. p->data=___________；5) s->data=t；

p->next
s->data

2． 设某棵完全二叉树中有100个结点，则该二叉树中有______________个叶子结点。

最后一个分支结点是n/2(下取整)＝k 所以叶子结点是n-k
100-50=50

3． 设某顺序循环队列中有m个元素，且规定队头指针F指向队头元素的前一个位置，队尾指针R指向队尾元素的当前位置，则该循环队列中最多存储_______队列元素。

问最多储存多少。
循环链表 只要头尾 不衔接，空一个元素， 判断空 和满就行了，所示是m-1

4． 对一组初始关键字序列（40，50，95，20，15，70，60，45，10）进行冒泡排序，则第一趟需要进行相邻记录的比较的次数为__________，在整个排序过程中最多需要进行__________趟排序才可以完成。

6 把95移到最后
8
在这里插入图片描述

5． 在堆排序和快速排序中，如果从平均情况下排序的速度最快的角度来考虑应最好选择_________排序，如果从节省存储空间的角度来考虑则最好选择________排序。

快速排序
堆排序

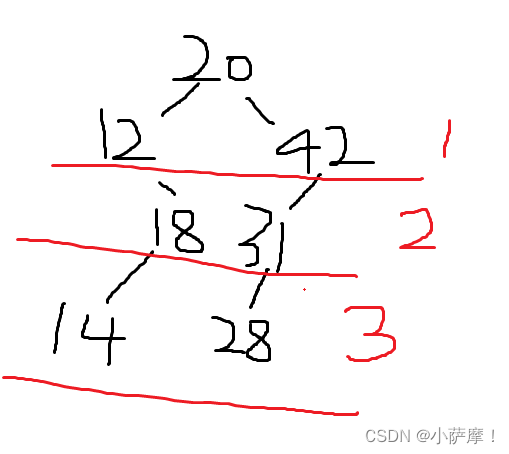
6． 设一组初始记录关键字序列为(20，12，42，31，18，14，28)，则根据这些记录关键字构造的二叉排序树的平均查找长度是_______________________________。

这里是引用
（1+2+2+3+3+4+4）/7=19/7

7． 设一棵二叉树的中序遍历序列为BDCA，后序遍历序列为DBAC，则这棵二叉树的前序序列为____________________。

CBDA

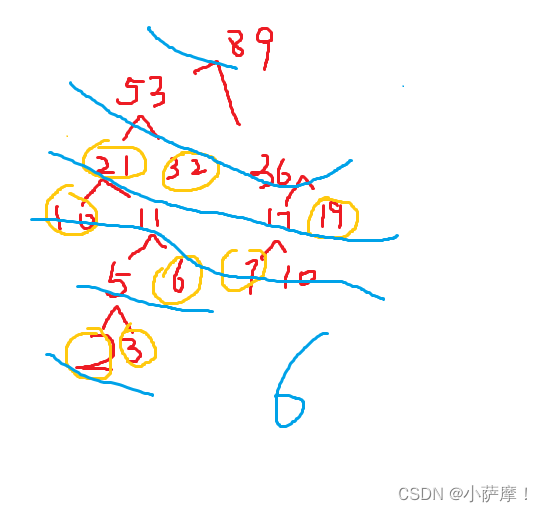
8.设用于通信的电文仅由8个字母组成，字母在电文中出现的频率分别为7、19、2、6、32、3、21、10，根据这些频率作为权值构造哈夫曼树，则这棵哈夫曼树的高度为________________。

这里是引用
6

9． 设一组记录关键字序列为(80，70，33，65，24，56，48)，则用筛选法建成的初始堆为_______________________。

(80,70,56,65,24,33,48)

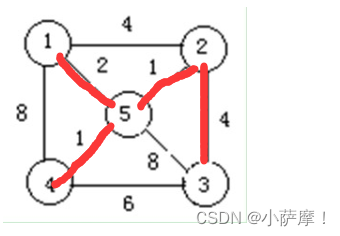
10． 设无向图G（如右图所示），则其最小生成树上所有边的权值之和为_________________。
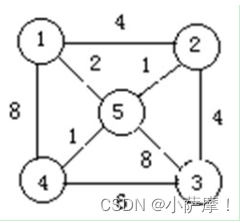
在这里插入图片描述

这里是引用
8

三、判断题(20分)

1． 有向图的邻接表和逆邻接表中表结点的个数不一定相等。( )

错
一定相等

2． 对链表进行插入和删除操作时不必移动链表中结点。( )

对，直接操作指针即可

3． 子串“ABC”在主串“AABCABCD”中的位置为2。( )

对

4． 若一个叶子结点是某二叉树的中序遍历序列的最后一个结点，则它必是该二叉树的先序遍历序列中的最后一个结点。( )

对 LMR MLR R的相对位置不变

5． 希尔排序算法的时间复杂度为O(n2)。( )

错。希尔排序的时间复杂度是O（nlogn）～O（n2）

6． 用邻接矩阵作为图的存储结构时，则其所占用的存储空间与图中顶点数无关而与图中边数有关。( )

错 都有关

7． 中序遍历一棵二叉排序树可以得到一个有序的序列。( )

LMR 对

8． 入栈操作和入队列操作在链式存储结构上实现时不需要考虑栈溢出的情况。( )

对 因为链表长度不是固定的

9． 顺序表查找指的是在顺序存储结构上进行查找。（ ）

错
顺序查找(Sequential Search)又叫线性查找，是最基本的查找技术，它的查找过程是：从表中第一个（或最后一个)记录开始，逐个进行记录的关键字和给定值比较，若某个记录的关键字和给定值相等，则查找成功，找到所查的记录；如果直到最后一个（或第一个）记录，其关键字和给定值比较都不等时，则表中没有所查的记录，查找不成功。
没说一定为数组

10．堆是完全二叉树，完全二叉树不一定是堆。（ ）

对

四、算法设计题(20分)

1．设计计算二叉树中所有结点值之和的算法。

void sum(bitree *bt,int &s)
{
   if(bt!=0) {
   s=s+bt->data; 
   sum(bt->lchild,s); 
   sum(bt->rchild,s);}	
}

2．设计将所有奇数移到所有偶数之前的算法。

void quickpass(int r[], int s, int t)
{
  int i=s,j=t,x=r[s];
  while(i<j)
{
    while (i<j && r[j]%2==0) j=j-1;  
    if (i<j) {r[i]=r[j];i=i+1;}
    while (i<j && r[i]%2==1) i=i+1;  
    if (i<j) {r[j]=r[i];j=j-1;}
  }
  r[i]=x;
}

3．设计判断单链表中元素是否是递增的算法。

int isriselk(lklist *head)
{
if(head==0||head->next==0) return(1);
else
for(q=head,p=head->next; p!=0; q=p,p=p->next)
if(q->data>p->data) return(0);
return(1);
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/370426.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

LeetCode:二叉树的最大深度104；559. N 叉树的最大深度

LeetCode:二叉树的最大深度104；559. N 叉树的最大深度

104. 二叉树的最大深度 给定一个二叉树&#xff0c;找出其最大深度。 二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。 说明: 叶子节点是指没有子节点的节点。 示例&#xff1a; 给定二叉树 [3,9,20,null,null,15,7]&#xff0c; 3/ \9 20/ \15 7 返回它的…
阅读更多...
看似平平无奇的00后，居然一跃上岸字节，表示真的卷不过......

看似平平无奇的00后，居然一跃上岸字节，表示真的卷不过......

又到了一年一度的求职旺季金&#xff01;三&#xff01;银&#xff01;四&#xff01;在找工作的时候都必须要经历面试这个环节。在这里我想分享一下自己上岸字节的面试经验&#xff0c;过程还挺曲折的&#xff0c;但是还好成功上岸了。大家可以参考一下&#xff01; 0821测评 …
阅读更多...
变则通--通则达--MindSpore社区活动-深度学习模型之数据变换-Transforms学习与体验记录

变则通--通则达--MindSpore社区活动-深度学习模型之数据变换-Transforms学习与体验记录

文章目录已加入 昇思MindSpore社区 证明截图安装 MindSpore 2.0 alpha 步骤打开powershell 或 cmd安装成功的截图实现 数据变换Transforms 任务Common Transforms 通用数据变换Vision Transforms 针对图像数据的变换Text Transforms 文本数据的变换Lambda Transforms结语已加入…
阅读更多...
Netty——序列化的作用及自定义协议

Netty——序列化的作用及自定义协议

序列化的作用及自定义协议序列化的重要性大小对比效率对比自定义协议序列化数据结构自定义编码器自定义解码器安全性验证NettyClientNettyServerNettyClientTestHandlerNettyServerTestHandler结果上一章已经说了怎么解决沾包和拆包的问题&#xff0c;但是这样离一个成熟的通信…
阅读更多...
【华为OD机试模拟题】用 C++ 实现 - 停车场最大距离（2023.Q1）

【华为OD机试模拟题】用 C++ 实现 - 停车场最大距离（2023.Q1）

最近更新的博客 【华为OD机试模拟题】用 C++ 实现 - 分积木（2023.Q1） 【华为OD机试模拟题】用 C++ 实现 - 吃火锅（2023.Q1） 【华为OD机试模拟题】用 C++ 实现 - RSA 加密算法（2023.Q1） 【华为OD机试模拟题】用 C++ 实现 - 构成的正方形数量（2023.Q1） 【华为OD机试模拟…
阅读更多...
MyBatis快速开发

MyBatis快速开发

查询user表中的所有数据 步骤&#xff1a; 创建user表 打开Navicat&#xff0c;新建查询&#xff0c;将下面SQL代码复制粘贴并执行&#xff1a; create database mybatis; use mybatis;drop table if exists tb_user;create table tb_user(id int primary key auto_incremen…
阅读更多...
抽象类与接口的区别

抽象类与接口的区别

抽象类什么是抽象类&#xff1f;抽象类是特殊的类&#xff0c;只是不能被实例化&#xff1b;除此以外&#xff0c;具有类的其他特性&#xff1b;重要的是抽象类可以包括抽象方法&#xff0c;这是普通类所不能的。抽象方法只能声明于抽象类中&#xff0c;且不包含任何实现&#…
阅读更多...
Docker安装YApi

Docker安装YApi

目录0、Docker 环境准备1、数据库准备 MongoDB2、启动 YAPI3、官网教程0、Docker 环境准备 Docker 容器之间网络互通需要使用 docker network create yapi 创建一个自定义网络 docker network create yapi1、数据库准备 MongoDB YAPI 的数据库是 MongoDB&#xff0c;准备镜像…
阅读更多...
Java线程池使用与原理解析1（线程池优点、使用方法、参数含义及线程池运转机制）

Java线程池使用与原理解析1（线程池优点、使用方法、参数含义及线程池运转机制）

为什么要使用线程池&#xff1f; JDK1.5后JUC包添加了线程池相关接口&#xff0c;在Java诞生之初并没有线程池这个概念。刚开始Java程序都是自行创建线程去处理任务。随着应用使用的线程越来越多&#xff0c;JDK开发者们发现有必要使用一个统一的类来管理这些线程&#xff0c;…
阅读更多...
从应届毕业生到大型开源社区 Committer，我做对了什么？

从应届毕业生到大型开源社区 Committer，我做对了什么？

熟悉李成龙的人都叫他小龙。“小龙&#xff0c;2.2.3 Milvus 版本&#xff0c;日志会一直积累在磁盘上吗&#xff1f;默认会定期清除吗&#xff1f;”“小龙&#xff0c;请教一个问题&#xff0c;为啥取不到 field 中的 type 字段&#xff1f;”“小龙……”熟悉 Milvus 社区群…
阅读更多...
django项目中如何添加自定义的django command

django项目中如何添加自定义的django command

项目目录 1.我们自己建立的application叫做app&#xff0c;首先在这个app目录下&#xff0c;我们需要新建management目录&#xff0c;这个目录里应该包括&#xff1a;__ init__.py&#xff08;内容为空&#xff0c;用于打包&#xff09;和commands目录&#xff0c;然后在comma…
阅读更多...
Linux中使用Docker部署Mysql数据库

Linux中使用Docker部署Mysql数据库

前言 和朋友一起搞一个项目&#xff0c;分了一下工作&#xff0c;但是mysql迟迟安装不上&#xff0c;程序都在一个环境里确实容易出现很多问题&#xff0c;浪费时间和经历在这些配置上&#xff0c;好在有docker了&#xff0c;就在docker里搭建一个Mysql数据库使用吧&#xff0…
阅读更多...
【计算机网络】计算机网络

【计算机网络】计算机网络

目录一、概述计算机网络体系结构二、应用层DNS应用文件传输应用DHCP 应用电子邮件应用Web应用当访问一个网页的时候&#xff0c;都会发生什么三、传输层UDP 和 TCP 的特点UDP 首部格式TCP 首部格式TCP 的三次握手TCP 的四次挥手TCP 流量控制TCP 拥塞控制三、网络层IP 数据报格式…
阅读更多...
李宏毅《机器学习》Bert笔记

李宏毅《机器学习》Bert笔记

李宏毅《机器学习》Bert笔记和工作原理解释1.参考2. self-supervised learning--bert3. bert的一些用法3.1情感分析3.2词性标注3.3常识推理和NLI3.4 QA问题4.bert的工作原理解释1.参考 bert论文 李宏毅《机器学习》自监督训练-bert 2. self-supervised learning–bert Bert模…
阅读更多...
图解JVM

图解JVM

1.JVM的一些概念 ​ JVM：Java虚拟机，可以存储代码以及在运行是可以动态调用一些指令的项目集。 ​ JDK：Java运行时所依赖的环境，[jar包、类]。 ​ JVM的作用：负责将.class文件解释成机器能够识别的机器码。 ​ JVM的位置：在操作系统之上，介于应用与系统之间。 ​ 机器码…
阅读更多...
python自动化测试学习路线（从入门到精通）

python自动化测试学习路线（从入门到精通）

目录&#xff1a;导读 一、Python的应用场景 二、自动化测试的那些事 三、主流自动化测试框架 三、Python自动化测试学习路线 写在最后 一、Python的应用场景 Python用于简单脚本编程&#xff0c;如编写2048小游戏或12306的自动抢票软件&#xff1b; Python用于系统编程&…
阅读更多...
数组（二）-- LeetCode[303][304] 区域和检索 - 数组不可变

数组（二）-- LeetCode[303][304] 区域和检索 - 数组不可变

1 区域和检索 - 数组不可变 1.1 题目描述 题目链接&#xff1a;https://leetcode.cn/problems/range-sum-query-immutable/ 1.2 思路分析 最朴素的想法是存储数组 nums 的值&#xff0c;每次调用 sumRange 时&#xff0c;通过循环的方法计算数组 nums 从下标 iii 到下标 jjj …
阅读更多...
javaEE 初阶 — 关于 IPv4、IPv6 协议、NAT（网络地址转换）、动态分配 IP 地址 的介绍

javaEE 初阶 — 关于 IPv4、IPv6 协议、NAT（网络地址转换）、动态分配 IP 地址 的介绍

文章目录1. IPv42. IPv63. NAT4. 动态分配 IP 地址1. IPv4 在互联网的世界中只有 0 和1 &#xff0c;所以每个人都有一个由 0 和 1 组成的地址来让别人找到你。 这段由 0 和 1 组成的地址叫 IP 地址&#xff0c;这是互联网的基础资源&#xff0c;可以简单的理解为互联网的土地。…
阅读更多...
《Qt 6 C++开发指南》简介

《Qt 6 C++开发指南》简介

我们编写的新书《Qt 6 C开发指南》在2月份终于正式发行销售了&#xff0c;这本书是对2018年5月出版的《Qt 5.9 C开发指南》的重磅升级。以下是本书前言的部分内容&#xff0c;算是对《Qt 6 C开发指南》的一个简介。1&#xff0e;编写本书的目的《Qt 5.9C开发指南》是我写的第一…
阅读更多...
（三）代表性物质点邻域的变形分析

（三）代表性物质点邻域的变形分析

本文主要内容如下&#xff1a;1. 伸长张量与Cauchy-Green 张量2. 线元长度的改变2.1. 初始/当前构型下的长度比2.2. 主长度比与 Lagrange/Euler 主方向2.3. 初始/当前构型下任意方向的长度比3. 线元夹角的改变4. 面元的改变5. 体元的改变1. 伸长张量与Cauchy-Green 张量 由于变…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023