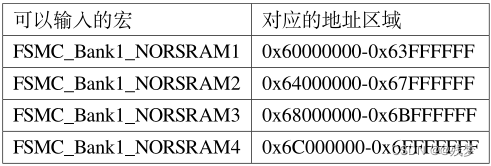
1.什么是损失函数

​         损失函数（Loss Function）又叫做误差函数，用来衡量算法拟合数据的好坏程度，评价模型的预测值与真实值的不一致程度，是一个非负实值函数，通常使用L(Y, f(x))​来表示，Y表示真实值，f(x)表示模型的预测值。损失函数越小，说明模型拟合的越好，模型的性能也越好。损失函数是经验风险函数的核心部分，也是结构风险函数重要组成部分。

2.常见的损失函数

​         机器学习通过对算法中的目标函数进行不断求解优化，得到最终想要的结果。分类和回归问题中，通常使用损失函数或代价函数作为目标函数。  损失函数可分为经验风险损失函数和结构风险损失函数。

        经验风险损失函数指预测结果和实际结果的差别，结构风险损失函数是在经验风险损失函数上加上正则项。 ​ 

       2-1 0-1损失函数 

        如果预测值和目标值相等，值为0，如果不相等，值为1。

        一般的在实际使用中，相等的条件过于严格，可适当放宽条件：

        2-2 绝对值损失函数

         和0-1损失函数相似，绝对值损失函数表示为：

        2-3 平方损失函数

        这点可从最小二乘法和欧几里得距离角度理解。最小二乘法的原理是，最优拟合曲线应该使所有点到回归直线的距离和最小。

        2-4 对数损失函数 

 ​        其中, Y 为输出变量, X为输入变量, L 为损失函数。 N为输入样本量, M为可能的类别数, yij 是一个二值指标, 表示类别 j 是否是输入实例 xi 的真实类别. pij 为模型或分类器预测输入实例 xi 属于类别 j 的概率.

        常见的逻辑回归使用的就是对数损失函数，有很多人认为逻辑回归的损失函数是平方损失，其实不然。逻辑回归它假设样本服从伯努利分布（0-1分布），进而求得满足该分布的似然函数，接着取对数求极值等。逻辑回归推导出的经验风险函数是最小化负的似然函数，从损失函数的角度看，就是对数损失函数。形式上等价于二分类的交叉熵损失函数。

        2-5 指数损失函数

        指数损失函数的标准形式为：

          AdaBoost就是以指数损失函数为损失函数。

2-6 交叉熵（cross-entropy）
 

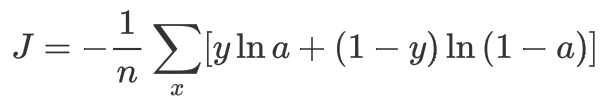
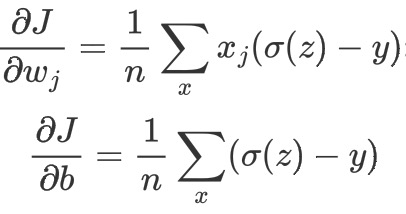
        当误差越大时，梯度就越大，权值w和偏置b调整就越快，训练的速度也就越快。
二次代价函数适合输出神经元是线性的情况，交叉熵代价函数适合输出神经元是S型函数的情况。