实现线性表的另一种常用方式就是基于链接结构，用链接关系显式表示元素之间的顺序关联。基于链接技术实现的线性表称为链接表或者链表。

        采用链接方式实现线性表的基本想法如下:

• 把表中的元素分别存储在一批独立的存储块（称为表的结点）里。
• 保证从组成表结构中的任一个结点可找到与其相关的下一个结点。
• 在前一结点里用链接的方式显式地记录与下一结点之间的关联。

        这样，只要能找到组成一个表结构的第一个结点，就能顺序找到属于这个表的其他结点。从这些结点里可以看到这个表中的所有元素。

        链接技术是一类非常灵活的数据组织技术，实现链表有多种不同的方式。下面首先讨论最简单的单链表，其中在每个表结点里记录着存储下一个表元素的结点的标识(引用/链接)。后面将介绍另外一些结构的链表，它们各有所长，支持不同的需要。在下面的讨论中，将把“存储着下一个表元素的结点”简称为“下一结点”。

1 单链表

        单向链接表（下面将简称为单链表或者链表）的结点是一个二元组，形式如下图a所示，其表元素域 elem 保存着作为表元素的数据项（或者数据项的关联信息），链接域 next 里保存同一个表里的下一个结点的标识。

        在最常见形式的单链表里，与表里的n个元素对应的n个结点通过链接形成一条结点链，如上图b所示。从引用表中首结点的变量（上图b中变量p）可以找到这个表的首结点，从表中任一结点可以找到保存着该表下一个元素的结点（表中下一结点），这样，从p出发就能找到这个表里的任一个结点。

        要想掌握一个单链表，就需要（也只需要）掌握这个表的首结点，从它出发可以找到这个表里的第一个元素（即在这个表结点里保存的数据，保存在它的 elem域中），还可以找到这个表里的下一结点（有关信息保存在这个结点的 next 域中）。按照同样的方式继续下去，就可以找到表里的所有数据元素。

        也就是说，为了掌握一个表，只需要用一个变量保存着这个表的首结点的引用（标识或称为链接）。今后将把这样的变量称为表头变量或表头指针。

小结一下：

• —个单链表由一些具体的表结点构成。
• 每个结点是一个对象，有自己的标识，下面也常称其为该结点的链接。
• 结点之间通过结点链接建立起单向的顺序联系。

        为了表示一个链表的结束，只需给表的最后结点（表尾结点）的链接域设置一个不会作为结点对象标识的值（称为空链接），在 Python 里自然可以用系统常量 None 表示这种情况，在上图里用接地符号“丄”表示链表结束，下面将一直这样表示。

        通过判断一个（域或变量的）值是否为空链接，可知是否已到链表的结束。在顺序扫描表结点时，应该用这种方法确定操作是否完成。如果一个表头指针的值是空链接，就说明“它所引用的链表已经结束”，这是没有元素就已结束，说明该表是空表。

        在实现链表上的算法时，并不需要关心在某个具体的表里各结点的具体链接值是什么（虽然保存在表结构里的值都是具体的），只需要关心链表的逻辑结构。对链表的操作也只需要根据链表的逻辑结构考虑和实现。

        为方便下面的讨论，现在定义个简单的表结点类：

class ListNode:
    def __init__(self, elem=0, next=None):
        self.elem = elem    
        self.next = next

1.1 基本操作

         创建空链表： 只需要把相应的表头变量设置为空链接，在Python语言中将其设置为None，在其他语言里也有惯用值，例如有的语言里用0作为这个特殊值。

         删除链表： 应丢弃这个链表里的所有结点。这个操作的实现与具体的语言环境有关。在一些语言（如C语言）里，需要通过明确的操作释放一个个结点所用的存储。在Python语言中这个操作很简单，只需简单地将表指针赋值为None，就抛弃了链表原有的所有结点。Python解释器的存储管理系统会自动回收不用的存储。

         判断表是否为空： 将表头变量的值与空链接比较。在Python语言中，就是检查相应变量的值是否为None.

         判断表是否满： 一般而言链表不会满，除非程序用完了所有可用的存储空间。

加入元素

        现在考虑给单链表加入元素的操作，同样有插入位置问题，可以做首端插入、尾端插人或者定位插人。不同位置的操作复杂度可能不同。

        首先应该注意，在链表里加入新元素时，并不需要移动已有的数据，只需为新元素安排一个新结点，然后根据操作要求，把新结点连在表中的正确位置。也就是说，插入新元素的操作是通过修改链接，接入新结点，从而改变表结构的方式实现的。

        表首端插入： 首端插入元素要求把新数据元素插入表中，作为表的第一个元素，这是最简单的情况。这一操作需要通过三步完成：

1. 创建一个新结点并存入数据（下图a表示要向表头变量 head 的链表加入新首元素13，为它创建了新结点，变量q指着该结点。这是实际插入前的状态）。

2. 把原链表首结点的链接存入新结点的链接域 next，这一操作将原表的一串结点链接在刚创建的新结点之后。

3. 修改表头变量，使之指向新结点，这个操作使新结点实际成为表头变量所指的结点，即表的首结点（上图b表示设置链接的这两步操作完成后的状态，新结点已成为 head 所指链表的首结点，13成为这个表的首元素。注意，示意图中链接指针的长度和形状都不表示任何意义，只有图中的链接指向关系有意义）。

        注意，即使在插入前head指向的是空表，上面三步也能正确完成工作。这个插人只是一次安排新存储和几次赋值，操作具有常量时间复杂度。

示例代码段：

q = ListNode(13)
q.next = head.next
head = q

         一般情况的元素插入： 要想在单链表里的某位置插入一个新结点，必须先找到该位置之前的那个结点，因为新结点需要插入在它的后面，需要修改它的next 域。如何找到这个结点的问题将在后面讨论，先看已经找到了这个结点之后怎样插入元素。

        设变量pre已指向要插入元素位置的前一结点，操作也分为三步:

1. 创建一个新结点并存入数据（下图a是实际插入前的状态）。
2. 把 pre 所指结点 next 域的值存入新结点的链接域 next，这个操作将原表在 pre 所指结点之后的一段链接到新结点之后。
3. 修改 pre 的 next 域，使之指向新结点，这个操作把新结点链入被操作的表，整个操作完成后的状态如下图b所示。

        注意，即使在插入前 pre 所指结点是表中最后一个结点，上述操作也能将新结点正确接入，作为新的表尾结点。

q = ListNode(13)
q.next = pre.next
pre.next = q

删除元素

        删除链表中元素，也可通过调整表结构删除表中结点的方式完成。这里也区分两种情况：删除表头结点的操作可以直接完成，删除其他结点也需要掌握其前一结点。

         删除表首元素： 删除表中第一个元素对应于删除表的第一个结点，为此只需修改表头指针，令其指向表中第二个结点。丢弃不用的结点将被Python解释器自动回收。

head = head.next

        一般情况的元素删除：一般情况删除须先找到要删元素所在结点的前一结点，设用变量pre指向，然后修改pre的next域，使之指向被删结点的下一结点。

pre.next = pre.next.next

        显然，这两个操作都要求被删结点存在。

        如果在其他编程语言里删除结点，还可能要自己释放存储。Python的自动存储管理机制能自动处理这方面的问题，使编程工作更简单，也保证了安全性。

扫描、定位和遍历

        在一般情况下插入和删除元素，都要求找到被删结点的前一结点。另外，程序里也可能需要定位链表中的元素、修改元素、逐个处理其中元素等。这些操作都需要检查链表的内容，实际上是检查表中的一些（或全部）结点。

        由于单链表只有一个方向的链接，开始情况下只有表头变量在掌握中，所以对表内容的一切检查都只能从表头变量开始，沿着表中链接逐步进行。这种操作过程称为链表的扫描，这种过程的基本操作模式是:

p = head
while p is not None and 还需继续的其他条件:
    对p所指结点里的数据做所需操作
    p = p.next

        根据Python语言的规定，这里的 p is not None 可以简单地只写一个 p。

        循环的继续（或结束）条件、循环中的操作由具体问题决定。循环中使用的辅助变量p称为扫描指针。注意，每个扫描循环必须用一个扫描指针作为控制变量，每步迭代前必须检查其值是否为None，保证随后操作的合法性。这与连续表的越界检查类似。

        上面表扫描模式是最一般的链表操作模式，下面介绍几个常用操作的实现。

         按下标定位： 按 Python 惯例，链表首结点的元素应看作下标0，其他元素依次排列。确定第i个元素所在结点的操作称为按下标定位，可以参考表扫描模式写出:

p = head
while p is not NOne and i > 0:
    i -= 1
    p = p.next

        假设循环前变量i已有所需的值，循环结束时可能出现两种情况：或者扫描完表中所有结点还没有找到第i个结点，或者p所指结点就是所需。通过检查 p 值是否为None可以区分这两种情况。显然，如果现在需要删除第k个结点，可以先将i设置为k-1，循环后检查i是0且p.next不是None就可以执行删除了。

         按元素定位： 假设需要在链表里找到满足谓词pred的元素。同样可以参考上面的表扫描模式，写出的检索循环如下:

p = head
while p is not None and not pred(p.elem):
    p = p.next

        循环结束时或者p是None；或者 pred(p.elem) 是 True，找到了所需元素。

        完整的扫描称为遍历，这样做通常是需要对表中每个元素做一些事情，例如:

p = head
while p is not None:
    print(p.elem)
    p = p.next

        这个循环依次输出表中各元素。只以条件 p is not None 控制循环，就能完成一遍完整的遍历。同样模式可用于做其他工作。

链表操作的复杂度
        总结一下链表操作的时间复杂度。

• 创建空表：$O(1)$。

• 删除表：在Python里是$O(1)$。当然，Python 解释器做存储管理也需要时间。

• 判断空表：$O(1)$。

• 加入元素（都需要加一个T(分配)的时间）

  • 首端加入元素：$O(1)$。
  • 尾端加入元素：$O(n)$、因为需要找到表的最后结点。
  • 定位加人元素：$O(n)$，平均情况和最坏情况。

• 删除元素:

  • 首端删除元素：$O(1)$。
  • 尾端删除元素：$O(n)$。
  • 定位删除元素：$O(n)$，平均情况和最坏情况。
  • 其他册除：通常需要扫描整个表或其一部分$O(n)$。

        扫描、定位或遍历操作都需要检查一批表结点，其复杂度受到表结点数的约束，都是 $O(n)$ 操作。其他在工作中有此类行为的操作也至少具有 $O(n)$ 时间复杂度。

求表的长度

        在使用链表时，经常需要求表的长度，为此可以定义一个函数:

p, n = head, 0
while p is not None:
    n += 1
    p = p.next
return n

        这个函数采用表扫描模式，遍历表中所有结点完成计数。显然，这个求表长度的算法所用时间与表结点个数成正比，具有 $O(n)$ 时间复杂度。

实现方式的变化

        以求表的长度为例，如果程序经常需要调用上面函数，$O(n)$ 复杂度就可能成为效率问题。如果表很长，执行该函数就可能造成可察觉的停顿。解决这个问题的一种方法是改造单链表的实现结构，增加一个表长度记录。显然，这个记录不属于任何表元素，是有关表的整体的信息。表示这件事的恰当方法是定义一种链表对象，把表的长度和表中的结点链表都作为这个表对象的数据成分，如下图所示。

        图中变星p指向表对象，这个对象的一个数据域记录表中元素个数（图中的20表示这个表当时有20个结点），另一个域引用着该表的结点链。采用了这种表示方式，求表长度的操作就可以简单返回元素计数域的值。但另一方面，这种表的每个变动操作都需要维护计数值。从整体看有得有失。这种调整消除了一个线性时间操作，可能在一些应用中很有意义。

1.2 单链表类的实现

自定义异常

        为能合理地处理一些链表操作中遇到的错误状态（例如，方法执行时遇到了无法操作的错误参数），首先为链表类定义一个新的异常类:

class LinkedListUnderflow(ValueError):
    pass

        这里把LinkedListUnderflow定义为标准异常类valueError的子类，准备在空表访问元索等场合抛出这个异常。在这些情况下抛出 valueError 也没问题，但定义了自己的异常类，就可以写专门的异常处理器，在一些情况下可能有用。

LList类的定义，初始化函数和简单操作

        现在基于结点类 ListNode 定义一个单链表对象的类，在这种表对象里只有一个引用链接结点的_head域，初始化为None表示建立的是一个空表。判断表空的操作检查_head；在表头插入数据的操作是prepend，它把包含新元素的结点链接在最前面；操作 pop 删除表头结点并返回这个结点里的数据：

class LList:
    def __init__(self):
        self._head = None

    def is_empty(self):
        return self._head is None

    def prepend(self, elem):
        self._head = ListNode(elem, self._head)

    def pop(self):
        if self._head is None:      # 无结点，引发异常
            raise LinkedListUnorderflow("in pop")
        e = self._head.elem
        self._head = self._head.next
        return e

        这里把 LList 对象的 _head 域作为对象的内部表示，不希望外部使用。上面定义里的几个操作都很简单，只有 pop 操作需要检查对象的状态，表中无元素时引发异常。

后端操作

        在链表的最后插入元素，必须先找到链表的最后一个结点。其实现首先是一个扫描循环，找到相应结点后把包含新元素的结点插入在其后。下面是定义:

def append(self, elem):
    if self._head is None:
        self._head = ListNone(elem)
        return 
    p = self._head
    while p.next is not None:
        p = p.next
    p.next = ListNode(elem)

        这里需要区分两种情况：如果原表为空，引用新结点的就应该是表对象的_head域，否则就是已有的最后结点的next域。两种情况下需要修改的数据域不一样。许多链表变动操作都会遇到这个问题，只有表首端插入/删除可以统一处理。

        现在考虑删除表中最后元素的操作，也就是要删除最后的结点。前面说过，要从单链表中删除一个结点，就必须找到它的前一结点。在尾端删除操作里，扫描循环应该找到表中倒数第二个结点，也就是找到p.next.next为None的p。下面定义的pop_last函数不仅删去表中最后元素，还把它返回（与pop统一）。

        在开始一般性扫描之前，需要处理两个特殊情况：如果表空没有可返回的元素时应该引发异常。表中只有一个元素的情况需要特殊处理，因为这时应该修改表头指针。一般情况是先通过循环找到位置，取出最后结点的数据后将其删除：

def pop_last(self):
    if self._head is None:      # 空表
        raise LinkeListUnderflow("in pop_last")
    
    p = self._head
    if p.next is None:          # 表中只有一个元素
        e = p.elem
        self._head = None
        return e
    while p.next.next is not None:  # 直到p.next是最后结点
        p = p.next
    e = p.next.elem
    p.next = None
    return e

        LList类的下一个方法是找到满足给定条件的表元素。这个方法有一个参数，调用时通过参数提供一个判断谓词，该方法返回第一个满足谓词的表元素。显然，这个操作也需要采用前面的基本扫描模式。定义如下：

def find(self, pred):
    p = self._head
    while p is not None:
        if pred(p.elem):
            return p.elem
        p = p.next

        最后一个方法非常简单，但实际中可能很有用。在开发一个表类的过程中，人们会经常想看看被操作的表的当时情况：

def print_all(self):
    p = self._head
    while p is not None:
        print(p.elem, end='')
        if p.next is not None:
            print(', ', end='')
        p = p.next
    print('')

2 循环单链表

        单链表的另一常见变形是循环单链表（简称循环链表），其中最后一个结点的next域不用None，而是指向表的第一个结点，如下图a所示。但如果仔细考虑，就会发现在链表对象里记录表尾结点更合适（如下图b），这样可以同时支持 $O(1)$ 时间的表头/表尾插入和 $O(1)$ 时间的表头删除。当然，由于循环链表里的结点连成一个圈，哪个结点算是表头或表尾，主要是概念问题，从表的内部形态上无法区分。

        循环单链表操作与普通单链表的差异就在于扫描循环的结束控制。易见，一些不变操作的实现也要修改，如 printall。

        这种表对象只需一个数据域 _rear，它在逻辑上始终引用着表的尾结点。前端加入结点，就是在尾结点和首结点之间加人新的首结点，尾结点引用不变。通过尾结点引用很容易实现这个操作。另一方面，尾端加入结点也是在原尾结点之后（与首结点之间）插人新结点，只是插入后要把它作为新的尾结点，因此需要更新尾结点引用。这两个操作都要考虑空表插入的特殊情况。对于输出表元素的操作，关键在于循环结束的控制。下面实现中比较扫描指针与表头结点的标识，到达了表头结点就结束。前端弹出操作也很容易实现，后端弹出操作需要通过一个扫描循环确定位置。

        下面循环单链表类定义只实现了几个典型方法，供参考：

class LCList:                   # 循环单链表类
    def __init__(self):
        self._rear = None

        def is_empty(self):
            return self._rear is None
        
        def prepend(self, elem):    # 前端插入
            p = LNode(elem)
            if self._rear is None:
                p.next = p          # 建立一个结点的环
                self._rear = p
            else:
                p.next = self._rear.next
                self.rear.next = p
        
        def append(self, elem):     # 尾插入
            self.prepend(elem)
            self._rear = self._rear.next

        def pop(self):  # 前端弹出
            if self._rear is None:
                raise LinkedListUnderflow("in pop of CLList")
            p = self._rear.next
            if self._rear is p:
                self._rear = None
            else:
                self._rear.next = p.next
            return p.elem
        
        def printall(self):     # 输出元素
            if self.is_empty():
                return
            p = self._rear.next
            while True:
                print(p.elem)
                if p is self._rear:
                    break
                p = p.next

3 双链表

        单链表只有一个方向的链接，只能做一个方向的扫描和逐步操作。即使增加了尾结点引用，也只能支持 $O(1)$ 时间的首端元素加入/删除和尾端加入。如果希望两端插入和删除操作都能高效完成，就必须修改结点（从而也是链表）的基本设计，加入另一方向的链接。这样就得到了双向链接表，简称双链表。有了结点之间的双向链接，不仅能支持两端的高效操作，一般结点操作也会更加方便。当然，这样做也需要付出代价：每个结点都需要增加一个链接域,增加的空间开销与结点数成正比，是 $O(n)$。如果每个表结点里的数据规模比较大，新增加的开销可能就显得不太重要了。

        为了支持首尾两端的高效操作，双链表应该采用下图所示的结构，包含一个尾结点引用域。易见，从双链表中任一结点出发，可以直接找到其前后的相邻结点（都是 $O(1)$ 操作）。而对单链表而言，只能方便地找到下一个结点，要找前一结点，就必须从表头开始逐一检查（通过一次扫描）。

        可以直接找到当前结点的前后结点，使得双链表的许多操作都很容易地进行。下面假定结点的下一结点引用域是next，前一结点引用域是prev。

结点操作

        先考虑结点删除。实际上，只要掌握着双链表里一个结点，就可以把它从表中取下，并把其余结点正确链接好。下图说明了这个操作。示例代码是：

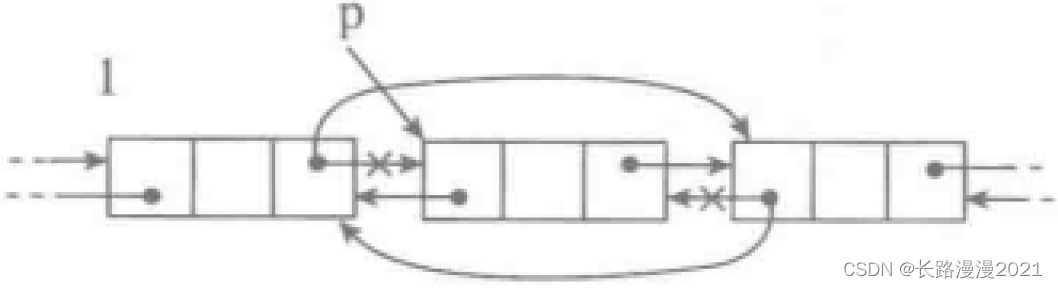
p.prev.next = p.next
p.next.prev = p.prev

        这两个语句使p所指结点从表中退出，其余结点保持顺序和链接。如果要考虑前后可能无结点的情况，只需增加适当的条件判断。

        在任一结点的前后加入结点的操作也很容易局部完成，只需掌握确定加入位置的这个结点。易见，加入一个结点需要做四次引用赋值。