传送门:牛客
题目描述:
Here comes the problem: Assume the sky is a flat plane. All the stars lie on it with a location (x, y). for each
star, there is a grade ranging from 1 to 100, representing its brightness, where 100 is the brightest and 1 is the
weakest. The window is a rectangle whose edges are parallel to the x-axis or y-axis. Your task is to tell where I
should put the window in order to maximize the sum of the brightness of the stars within the window. Note, the
stars which are right on the edge of the window does not count. The window can be translated but rotation is
not allowed.
输入:
3 5 4
1 2 3
2 3 2
6 3 1
3 5 4
1 2 3
2 3 2
5 3 1
输出:
5
6
一道有关扫描线的题目.假设你扫描线算法并不会,那么可以去学一下扫描的算法再来做这道题关于扫描线算法,网上有大量博客对此进行讲解,此处就不在赘述了.
关于这道题,绝大部分题解对于矩形的建立都是一笔带过,并且往往都是将星星当做矩形的左下顶点,这样做的原因却几乎没有一个详细的解释,读者难免感到无法读懂.
对于一颗星星,此时我们想一下假设一个
w
∗
h
w*h
w∗h的矩形能够罩住他,此时考虑一下都是什么情况,我们考虑一下极限情况,我们会发现是一下这种情况(中间为星星):
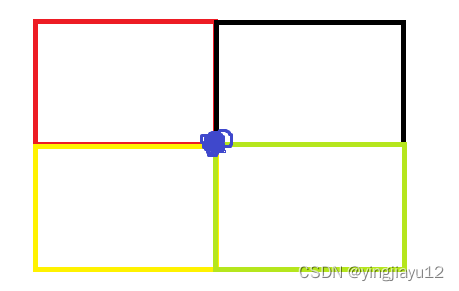
也就是从右上角开始的黑色矩形最远平移到红色矩形的位置,最下平移到黄色矩形的位置.那么此时我们会发现对于一颗星星和一个矩形来说,只要这个矩形的右上角在我们的黑色矩形位置,此时形成的矩形肯定就能包裹住我们的星星,但是注意此时我们的题面中说在矩形的边框上的星星是不满足的.又因为两个题面上说坐标和矩形长宽都是整数,这个意味着两个星星的横坐标距离大于等于1.所以此时我们可以将矩形的长宽缩小1,[想一下,对于左右两个星星来说,假设他们距离x,那么此时我们的矩形的长必然是要大于才行,又因为是整数,所以此时长至少为x+1.所以此时我们选择将长缩小1,这样的话对于我们删减后的矩形来说,星星在边框上时合法的,就变得易于操作了.]
那么对于所有的星星来说,我们都以这个星星作为我们的新矩形的左下顶点来建立矩形,以亮度作为矩形的贡献.通过我们之前的分析可以发现,我们最终的贡献其实就是矩形重叠的亮度的最大值.此时我们可以使用扫描线的思想来做这道题,以矩形上下边为扫描线,下边权为正,上边权为负开始从下往上扫并且维护区间最大值即可.
注意点:在扫描线从下往上扫的过程中遇到y值相同的扫描线应采取先减再加的原则(在牛客上因为数据比较弱并没有卡这个点,很多人可能都注意不到)
优化&巧妙的想法:对于这种只需要区间[1,n]的维护值来说,我们建立线段树的时候可以不使用pushdown(因为我们根本不需要关注子节点是怎么样的),在子节点pushup的时候将父节点对子节点的lazy加上即可.
注意,此方法在我看来并不具有很强的意义,虽然省去了对子节点的维护,码量减少了,但是因为这种方式大大的修改了模板,会导致出现一写奇奇怪怪的错误甚至思维上的混乱,但是在平时可以挑战一下,这样改变常规的做法可以大大增强自己对线段树的理解
下面是具体的代码部分(标准版维护版):
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {
ll x=0,w=1;char ch=getchar();
for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;
for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';
return x*w;
}
#define int long long
#define maxn 1000000
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
struct Segment_tree{
int l,r,mx,lazy;
}tree[maxn*4];
int n,w,h;
struct Line{
int l,r,y,cate;
bool operator < (const Line &rhs) const {
if(y==rhs.y) return cate<rhs.cate;
else return y<rhs.y;
}
}line[maxn];
vector<int>v;
int Get_id(int x) {
return lower_bound(v.begin(),v.end(),x)-v.begin()+1;
}
void build(int l,int r,int rt) {
tree[rt].l=l;tree[rt].r=r;
if(l==r) return ;
int mid=(l+r)>>1;
build(lson);build(rson);
}
void pushup(int rt) {
tree[rt].mx=max(tree[ls].mx,tree[rs].mx);
}
void change(int rt,int val) {
tree[rt].mx+=val;tree[rt].lazy+=val;
}
void pushdown(int rt) {
change(ls,tree[rt].lazy);change(rs,tree[rt].lazy);
tree[rt].lazy=0;
}
void update(int l,int r,int val,int rt) {
if(tree[rt].l==l&&tree[rt].r==r) {
change(rt,val);
return ;
}
if(tree[rt].lazy) pushdown(rt);
int mid=(tree[rt].l+tree[rt].r)>>1;
if(r<=mid) update(l,r,val,ls);
else if(l>mid) update(l,r,val,rs);
else update(l,mid,val,ls),update(mid+1,r,val,rs);
pushup(rt);
}
signed main() {
while(scanf("%lld%lld%lld",&n,&w,&h)!=EOF) {
v.clear();int cnt=0;
for(int i=1;i<=n;i++) {
int x=read(),y=read(),val=read();
line[++cnt].l=x;line[cnt].r=x+w;
line[cnt].y=y;line[cnt].cate=val;
line[++cnt].l=x;line[cnt].r=x+w;
line[cnt].y=y+h;line[cnt].cate=-val;
v.push_back(x);v.push_back(x+w);
}
sort(line+1,line+2*n+1);
sort(v.begin(),v.end());
v.erase(unique(v.begin(),v.end()),v.end());
int Size=v.size();
build(1,Size,1);
int ans=-ll_INF;
for(int i=1;i<=2*n;i++) {
int x=Get_id(line[i].l),x2=Get_id(line[i].r);
update(x,x2-1,line[i].cate,1);
ans=max(ans,tree[1].mx);
}
printf("%lld\n",ans);
}
return 0;
}
下面是具体的代码部分(省略 p u s h d o w n pushdown pushdown版):
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {
ll x=0,w=1;char ch=getchar();
for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;
for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';
return x*w;
}
#define int long long
#define maxn 1000010
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
struct Segment_tree{
int l,r,mx,lazy;
}tree[maxn*4];
int n,w,h;
struct Line{
int l,r,y,cate;
bool operator < (const Line &rhs) const {
if(y==rhs.y) return cate<rhs.cate;
else return y<rhs.y;
}
}line[maxn];
vector<int>v;
int Get_id(int x) {
return lower_bound(v.begin(),v.end(),x)-v.begin()+1;
}
void build(int l,int r,int rt) {
tree[rt].l=l;tree[rt].r=r;tree[rt].mx=0;tree[rt].lazy=0;
if(l==r) return ;
int mid=(l+r)>>1;
build(lson);build(rson);
}
void pushup(int rt) {
tree[rt].mx=max(tree[ls].mx+tree[rt].lazy,tree[rs].mx+tree[rt].lazy);
}
void update(int l,int r,int val,int rt) {
if(tree[rt].l==l&&tree[rt].r==r) {
tree[rt].mx+=val;tree[rt].lazy+=val;
return ;
}
int mid=(tree[rt].l+tree[rt].r)>>1;
if(r<=mid) update(l,r,val,ls);
else if(l>mid) update(l,r,val,rs);
else update(l,mid,val,ls),update(mid+1,r,val,rs);
pushup(rt);
}
signed main() {
while(scanf("%lld%lld%lld",&n,&w,&h)!=EOF) {
v.clear();int cnt=0;
for(int i=1;i<=n;i++) {
int x=read(),y=read(),val=read();
line[++cnt].l=x;line[cnt].r=x+w;
line[cnt].y=y;line[cnt].cate=val;
line[++cnt].l=x;line[cnt].r=x+w;
line[cnt].y=y+h;line[cnt].cate=-val;
v.push_back(x);v.push_back(x+w);
}
sort(line+1,line+2*n+1);
sort(v.begin(),v.end());
v.erase(unique(v.begin(),v.end()),v.end());
int Size=v.size();
build(1,Size,1);
int ans=-ll_INF;
for(int i=1;i<=2*n;i++) {
int x=Get_id(line[i].l),x2=Get_id(line[i].r);
update(x,x2-1,line[i].cate,1);
ans=max(ans,tree[1].mx);
}
printf("%lld\n",ans);
}
return 0;
}



![[AI助力] 2022.2.23 考研英语学习 2010 英语二翻译](https://img-blog.csdnimg.cn/d4984061e48a44a4bbb13eb38e258085.png)