要么庸俗,要么孤独…

文章目录
- 一、仅仅反转字母
- 二、字符串中的第一个唯一字符(计数排序的思想)
- 三、字符串相加(做好加进位的工作即可)
- 四、把字符串转换成整数
- 五、反转字符串中的单词 III
- 六、字符串相乘(高精度算法:大数乘法)
- 七、验证一个字符串是否为回文
- 八、反转字符串 II(反转字符串2k区间的前k个字符)
- 九、字符串中最后一个单词的长度(getline()的使用)
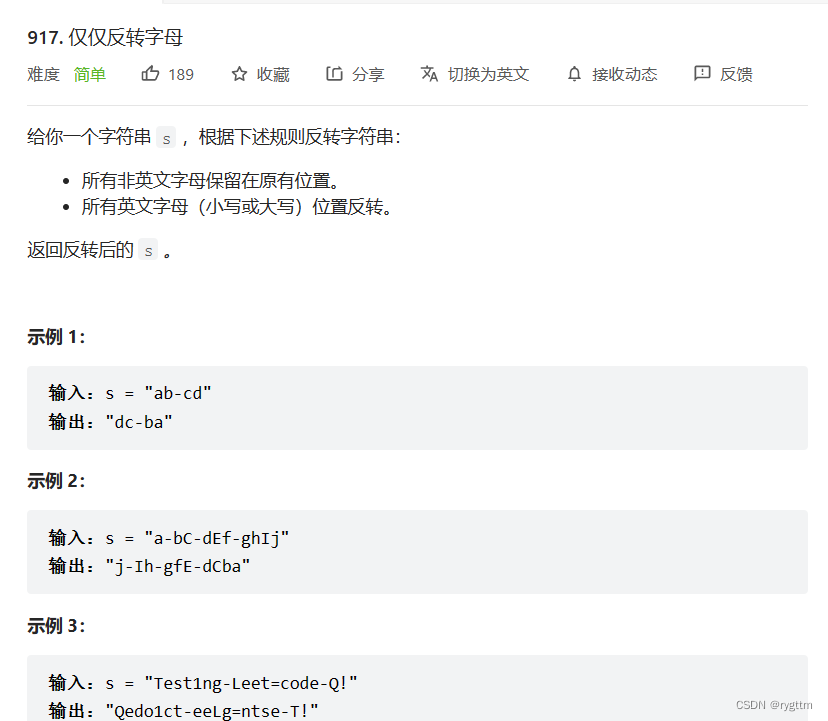
一、仅仅反转字母
1.
这道题的难度算非常简单的了,我们可以定义两个变量来表示数组首尾位置的有效字符的下标,然后分别从前和从后向中间遍历,只要遇到字母就停下来,利用库函数swap进行交换。
class Solution {
public:
string reverseOnlyLetters(string s) {
size_t begin=0,end=s.size()-1;
while(begin<end)
{
while(begin<end && !isalpha(s[begin]))
//字符串有可能全不是字母,begin要保证小于end,否则陷入死循环
{
++begin;
}
while(begin<end && !isalpha(s[end]))
{
--end;
}
swap(s[begin],s[end]);
++begin;
--end;
}
return s;
}
};
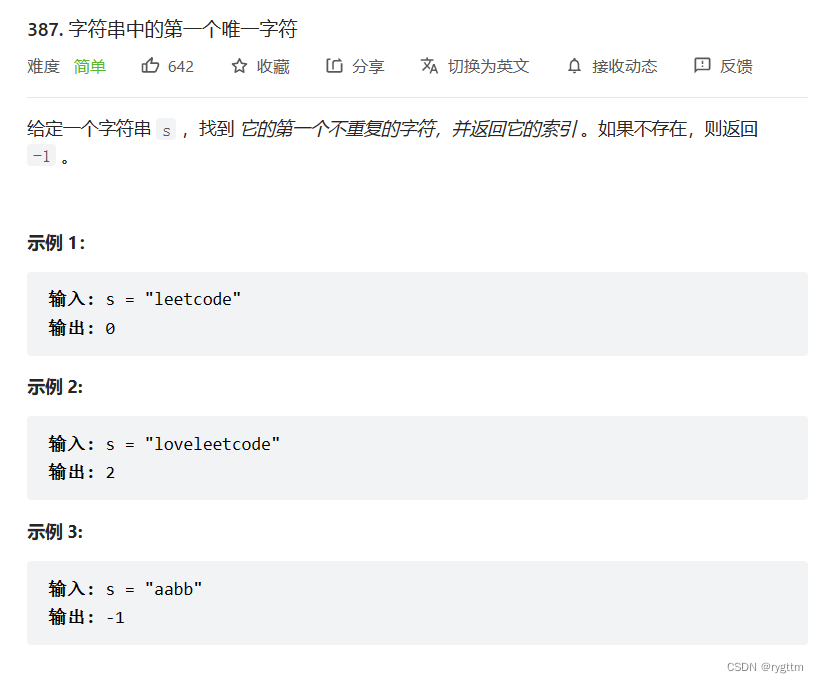
二、字符串中的第一个唯一字符(计数排序的思想)
1.
这道题利用了计数排序的思想,每一个字母对应的ascll码本质都是一个数字,我们可以将这个数字看成是计数数组count的下标,然后将这个下标对应的元素+1,这样数组count中如果有某个下标对应的元素是1,则证明这个下标的ascll码反推回去的字母在原字符串中只出现了一次,然后再将字符串数组从前向后遍历一遍,看看第几个字符在计数数组里面的字符下标对应的元素是1,如果从前向后遍历的过程中遇到这样的字符,则说明这个字符就是字符串中的第一个唯一字符,然后直接返回即可。
class Solution {
public:
int firstUniqChar(string s) {
int count[128]={0};
int size=s.size();
for(int i=0;i<size;i++)
{
count[s[i]]++;
}
for(int i=0;i<size;i++)
{
if(1==count[s[i]])
{
return i;
}
}
return -1;
}
};
class Solution {
public:
int firstUniqChar(string s) {
int count[26]={0};
for(auto ch : s)
{
count[ch - 'a']++;
}
for(int i = 0; i < s.size(); i++)
{
if(count[s[i] - 'a'] == 1)
return i;
}
return -1;
}
};
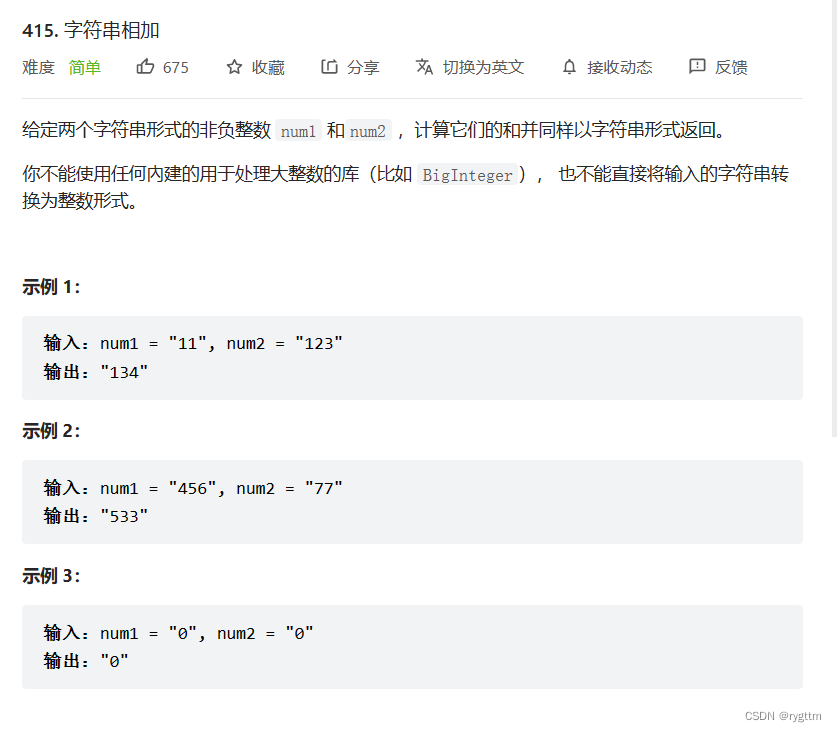
三、字符串相加(做好加进位的工作即可)
1.
越是这样逻辑链比较长的题目,我们越应该多定义几个变量,因为有效变量越多,我们的思维负担就越小,逻辑就更加清晰。当然,多做题和阅读高级代码也是非常重要的因素,这可以帮助我们定义出多个有效的变量。
2.
对于出现两种判断情况时,要善于运用三目运算符,这可以帮助我们减少if的分支条件判断,影响我们的思维逻辑。
3.
无论是数的加减还是乘除,在计算高位时都不要忘了加上前面的进位,比头插效率更高的是尾插,我们可以先尾插成返回的结果字符串,然后利用库函数模板reverse传递字符串首尾的迭代器即可反转字符串,这样的时间复杂度是O(N),而头插的时间复杂度是O(N²)。
class Solution {
public:
string addStrings(string num1, string num2) {
string retstr;
int carry=0;
int end1 = num1.size()-1,end2 = num2.size()-1;
while(end1 >= 0 || end2 >= 0)
{
int value1 = end1 >= 0 ? num1[end1]-'0' : 0;
int value2 = end2 >= 0 ? num2[end2]-'0' : 0;
int ret = value1 + value2 + carry;
//表示下一位计算时,要加上前面位的进位。
carry = ret/10;
ret %= 10;
retstr.insert(0, 1, ret + '0');
//用'ret'来进行头插,会发生int到char类型的截断,不要胡搞。
--end1;
--end2;
}
if(carry == 1)
retstr.insert(0, 1, '1');
return retstr;
}
};
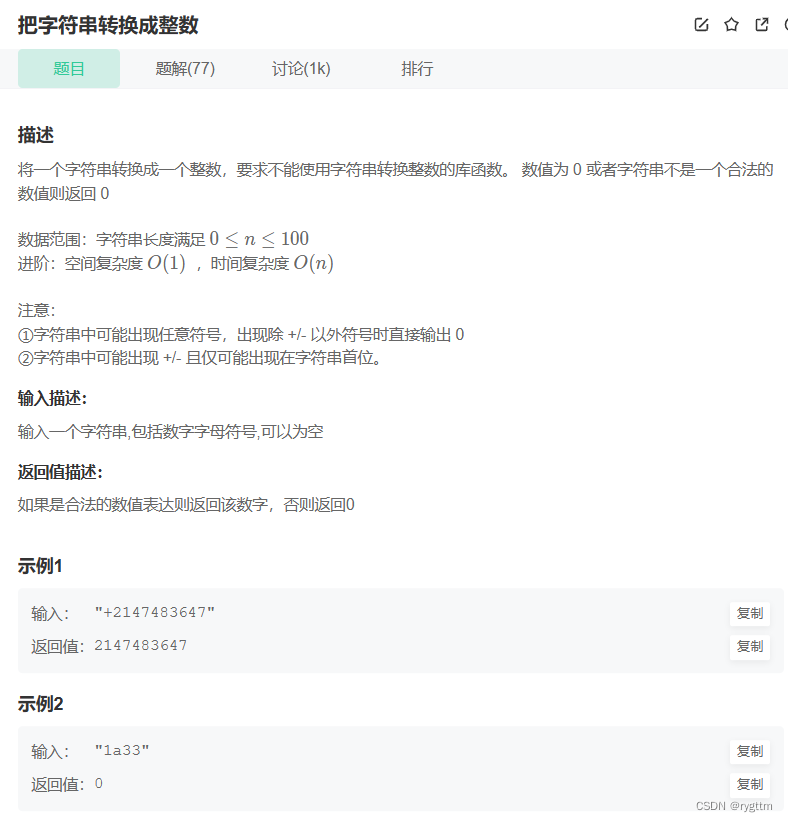
四、把字符串转换成整数
1.
可以从后向前进行遍历字符串,将每个字符转换成整数,然后乘上相应的位权重,这个位权重我们可以自己实现mypow函数,因为库提供的pow函数返回的是double类型的数据。最后将每一位字符对应的整数加到ret上即可。
class Solution {
public:
int mypow(int num, int cnt)
{
int ret = 1;
while(cnt>0)
{
ret *= num;
cnt--;
}
return ret;
}
int StrToInt(string str) {
int retnum = 0;
int size = str.size();
int end = str.size()-1;
if(str[end] == '+' || str[end] == '-')
return 0;
//从后向前进行遍历,将字符对应的数字加到retnum即可
while(end >= 0 && (
(str[end] >= '1' && str[end] <= '9')
|| str[end] == '+'
|| str[end] == '-'))
{
int num = (str[end] - '0') * mypow(10, size - end -1);
retnum += num;
--end;
if(end == 0 && str[end] == '-')
{
retnum *= -1;
return retnum;
}
if(end ==0 && str[end] == '+')
{
return retnum;
}
}
if(end >= 0)
return 0;
return retnum;
}
};
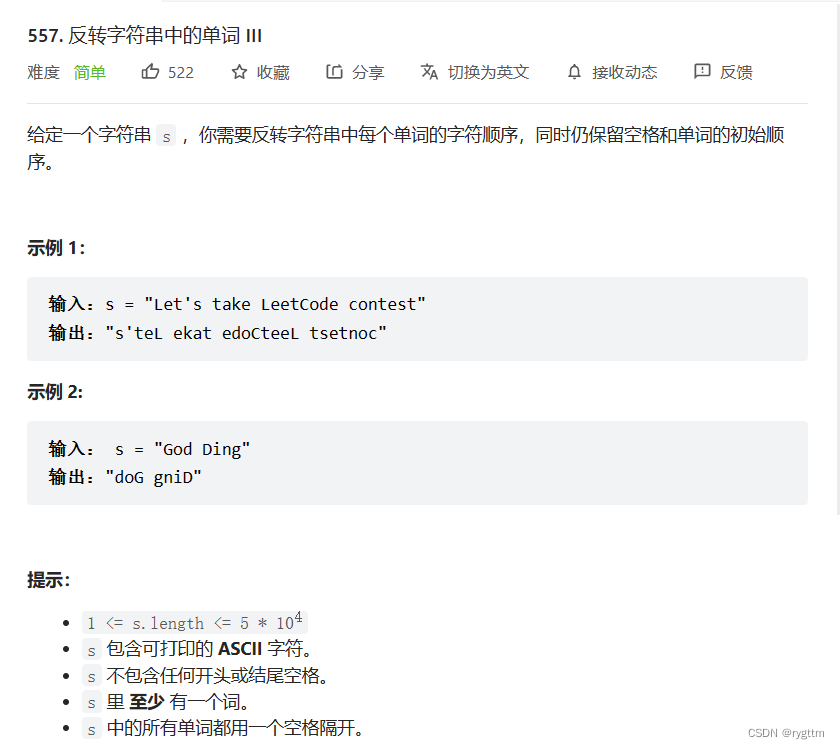
五、反转字符串中的单词 III
1.
这道题本质思想还是前后指针,end作为前指针,我们让他的下一个位置指向空格,并且拿一个flag记录一下空格的位置,以便于之后begin和end的迭代。
所以只要每次将begin和end之间的字符进行反转即可,反转完毕之后,让begin和end向后迭代直到最后一部分单词被反转完毕。
class Solution {
public:
string reverseWords(string s) {
int begin = 0, end = 0;
int size = s.size() - 1;
while(begin <= size && s[end] != '\0')
{
while(s[end+1] != ' ')
{
if(s[end + 1] == '\0')
break;
++end;
}
int flag = end + 1;//flag是空格的位置
while(begin < end)
{
swap(s[begin++], s[end--]);
}
begin = flag + 1;
end = begin;
}
return s;
}
};
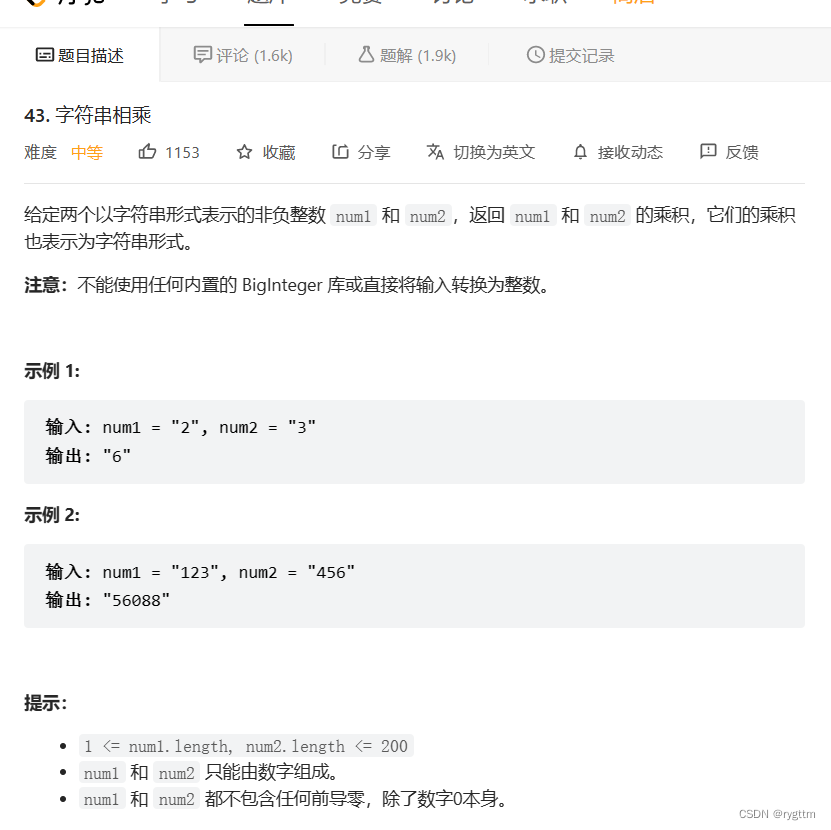
六、字符串相乘(高精度算法:大数乘法)
1.
利用reverse和迭代器先将两个字符串都进行反转,然后遍历其中一个字符串,由地位向高位拿出字符并且将每个字符与另一个字符串进行相乘,将相乘后的字符串结果暂时存到tmp对象里面,然后将tmp字符串错位相加到result字符串里面,第一次不用错位相加,但之后每一次相乘的结果都需要进行错位相加。

class Solution
{
public:
void MulItem(string &tmp, string &num1, char a)
{
int i = 0, sign=0;
int mul = 0;
while(i < num1.size())
{
mul = (num1[i]-'0') * (a-'0') + sign;
if(mul >= 10)
{
sign = mul / 10;
mul %= 10;
}
else
sign = 0;
tmp.push_back(mul+'0');
i++;
}
if(sign > 0)
tmp.push_back(sign+'0');
}
//对应位相加,sign进位采用引用传递
int AddItem(int a, int b, int &sign)
{
int add = a+b+sign;
if(add >= 10)
{
sign = 1;
add -= 10;
}
else
sign = 0;
return add;
}
//错位相加
void MoveAdd(string &result, string &tmp, int k)
{
int i, j;
i = k;
j = 0;
int sign = 0;
while(i<result.size() &&j<tmp.size())
{
result[i] = AddItem(result[i]-'0', tmp[j]-'0', sign) + '0';
i++;
j++;
}
if( i<result.size()&&sign)//在错位相加之后,下一次的tmp字符串可能为0,这个时候需要在原有的result字符串的基础上进行上一次result和tmp字符串相加之后可能遗留下来的进位。
result[i] = AddItem(result[i]-'0', 0, sign)+'0';
while(j < tmp.size())//如果tmp字符串不为0,则错位相加之后,tmp字符串肯定还没有遍历完,所以还需要将剩余的字符在加到result上面去(利用push_back)
{
int v = AddItem(0, tmp[j]-'0', sign);
result.push_back(v+'0');
j++;
}
if(sign)//最后的最后,如果在tmp的剩余字符串加完之后,还留有进位,则需要继续将进位尾插到result字符串对象里面
result.push_back(sign+'0');
}
string multiply(string num1, string num2)
{
//先翻转数据,方便进位处理
reverse(num1.begin(), num1.end());
reverse(num2.begin(), num2.end());
string tmp, result;
for(int i=0; i<num2.size(); ++i)
{
//使用num2的每一个数据乘以num1
MulItem(tmp, num1, num2[i]);
//将乘得的结果进行错位相加
MoveAdd(result, tmp, i);
tmp.clear();
}
while(result.size()!=1 && result.back()=='0')//如果进位之后的字符串尾部出现0,我们需要手动将其pop掉
result.pop_back();
//翻转数据,恢复数据
reverse(result.begin(), result.end());
return result;
}
};
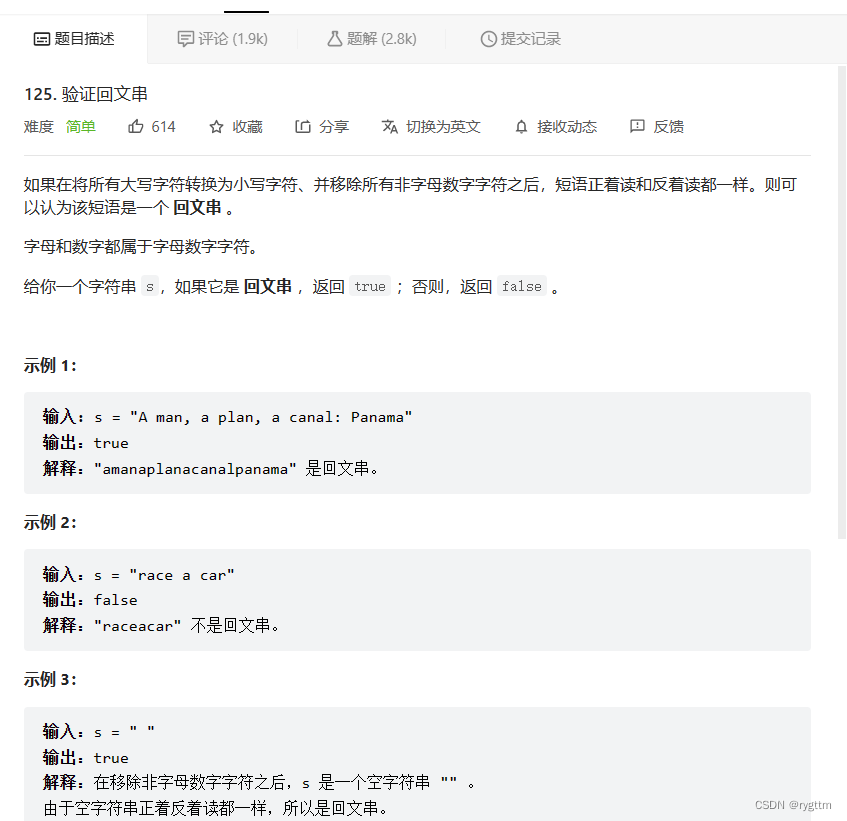
七、验证一个字符串是否为回文
1.
这道题有两种解决方式,第一种就是将所有的字母和数字字符挑出来尾插到一个新的string类对象中,然后我们从对象的头和尾向中间进行遍历,判断是否为回文串。
第二种就是直接原地在原有字符串中进行比较,遍历的同时过滤掉非字母和数字的字符即可。注意判断一下没有字母或数字的情况,这样的情况我们直接返回true即可。
class Solution {
public:
bool isPalindrome(string s) {
// string palin_array;
// int begin1 = 0, end1 = s.size() - 1;
// //1.先将字符串中大写字母替换为小写字母
// for(int i = begin1; i <= end1; i++)
// {
// if(s[i] >= 'A' && s[i] <= 'Z')
// s[i] += 32;
// }
// //2.将字母和数字放到palin_array数组里面
// for(int i = begin1; i <= end1; i++)
// {
// if(s[i] >= 'a' && s[i] <= 'z' || s[i] >= '0' && s[i] <= '9')
// palin_array.push_back(s[i]);
// }
// if(palin_array.size() == 0)
// return true;
// int begin2 = 0, end2 = palin_array.size() - 1;
// int palin_tail = palin_array.size() - 1;
// //3.判断palin_array数组的字符串是否是回文
// while(begin2 != palin_tail)
// {
// if(palin_array[begin2] != palin_array[end2])
// return false;
// begin2++;
// end2--;
// }
// return true;
//1.先将字符串中大写字母替换为小写字母
int begin1 = 0, end1 = s.size() - 1, tail = s.size() - 1;
for(int i = begin1; i <= end1; i++)
{
if(s[i] >= 'A' && s[i] <= 'Z')
s[i] += 32;
}
//2.在s数组里直接进行首尾元素的比较
while(begin1 <= tail)
{
while(!(s[begin1] >= 'a' && s[begin1] <= 'z' ||
s[begin1] >= '0' && s[begin1] <= '9') && begin1 <= tail)
{
begin1++;
if(begin1 > tail )
return true;
}
while(!(s[end1] >= 'a' && s[end1] <= 'z' ||
s[end1] >= '0' && s[end1] <= '9') && end1 >= 0)
{
end1--;
}
if(s[begin1] != s[end1])
{
return false;
}
//如果字符相等,继续进行比较
begin1++;
end1--;
}
return true;
}
};
八、反转字符串 II(反转字符串2k区间的前k个字符)
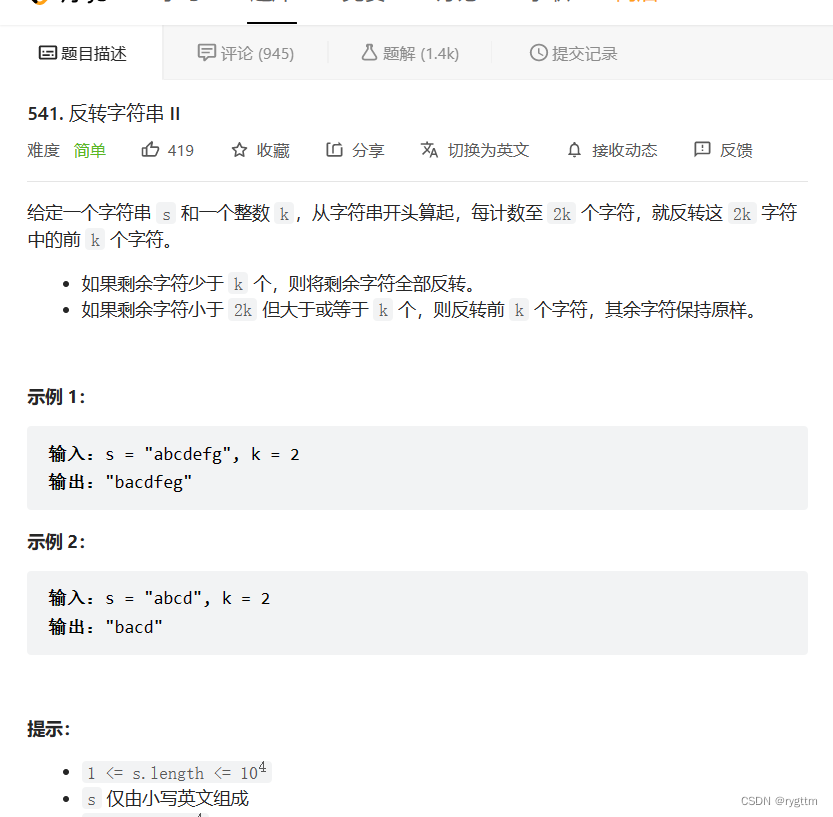
1.这道题的逻辑非常的清晰,我们只需要找到凑成2k大小的字符组,然后按照前后指针的方法进行每组当中前k个字符的反转,最后剩余的字符分为两种情况分别进行处理,处理的方式也很简单,详情见代码。
2.
这道题的难度不大,但是在我做的时候,发生了一些代码逻辑的小问题,并且在我多次走读代码之后依旧找不到漏洞,所以这很是让我苦恼。
就算是调试,对于这样的接口型,我们也不好调试,因为如果要进行调试,还需要自己补充成员变量,相当的麻烦,但其实这样的接口型调试也有解决方法,我们只需要将其搞成类静态函数即可,然后在main函数里面用类名加域作用限定符调用这个静态函数即可,这样就可以轻松实现调试了,对于接口型,搞成静态这样的方法非常好用,可以不用定义类对象就能调用成语函数,岂不快哉!
3.
这里在复习一下关于类的静态成员的知识,关于类静态成员的调用方式分为两种,一种是通过对象.静态成员方式调用,一种是通过类名::静态成员的方式进行调用。
而对于非静态成员来讲,不能通过类名::的方式进行调用,因为非静态成员函数有this指针,所以在调用时必须指定调用的对象是谁,正因为如此,没有this指针的静态成员函数才可以通过类名进行调用。以此来方便我们进行调试
class Solution {
public:
static string reverseStr(string s, int k) {
//1.先判断这个字符串中有几个凑成2k大小的字符组,留下的字符个数是多少
int group_cnt = s.size() / (2 * k);
int remaining_char = s.size() % (2 * k);
//2.将前group_cnt个字符组每每进行字符反转
int prev_begin1 = 0, prev_end1 = k - 1;
while (group_cnt--)
{
//记录原先begin1和end1的位置,下面循环的时候,begin1和end1会发生改变
int begin1 = prev_begin1, end1 = prev_end1;
while (begin1 < end1)
{
swap(s[begin1++], s[end1--]);
}
prev_begin1 += (2 * k);
prev_end1 += (2 * k);
}
//3.将剩余的字符分为两种情况,然后进行反转
int begin2 = s.size() - remaining_char;
int end2 = s.size() - 1;
if (remaining_char < k)//剩余字符全部反转
{
while (begin2 < end2)
swap(s[begin2++], s[end2--]);
}
else//反转剩余字符的前k个字符
{
int end3 = end2 - (remaining_char - k);
while (begin2 < end3)
swap(s[begin2++], s[end3--]);
}
return s;
}
};
九、字符串中最后一个单词的长度(getline()的使用)
1.这道题可以利用getline来获取一行的字符串,然后通过rfind函数找到最后一个单词前面空格的位置,最后用字符串大小(实际就是\0位置的下标)减去空格位置的下标,再减1,因为两个下标做差求的是区间的个数,要求区间中字符的个数需要多减去1.
#include <iostream>
#include <string>
using namespace std;
int main()
{
string str;
getline(cin,str);
int pos = str.rfind(' ');
cout << str.size() - pos - 1 << endl;
}