使用FORCE训练的脉冲神经网络中的监督学习（Matlab代码实现）

news2025/10/28 9:12:12

💥1 概述

📚2 运行结果

🎉3 参考文献

👨‍💻4 Matlab代码

💥1 概述

1.1 脉冲神经网络简介

脉冲神经网络 (SNN) 属于第三代神经网络模型，实现了更高级的生物神经模拟水平。除了神经元和突触状态之外，SNN 还将时间概念纳入了其操作之中，是一种模拟大脑神经元动力学的一类很有前途的模型。

那么什么是第一代和第二代神经网络模型呢？

1.1.1 第一代神经网络

第一代神经网络又称为感知器，在1950年左右被提出来，它的算法只有两层，输入层输出层，主要是线性结构。它不能解决线性不可分的问题，对稍微复杂一些的函数都无能为力，如异或操作。

1.1.2 第二代神经网络：BP 神经网络

为了解决第一代神经网络的缺陷，在1980年左右 Rumelhart、Williams 等人提出第二代神经网络多层感知器 (MLP)。和第一代神经网络相比，第二代在输入层之间有多个隐含层的感知机，可以引入一些非线性的结构，解决了之前无法模拟异或逻辑的缺陷。

第二代神经网络让科学家们发现神经网络的层数直接决定了它对现实的表达能力，但是随着层数的增加，优化函数愈发容易出现局部最优解的现象，由于存在梯度消失的问题，深层网络往往难以训练，效果还不如浅层网络。

所有对目前机器学习有所了解的人都听说过这样一个事实：目前的人工神经网络是第二代神经网络。它们通常是全连接的，接收连续的值，输出连续的值。尽管当代神经网络已经让我们在很多领域中实现了突破，但它们在生物学上是不精确的，其实并不能模仿生物大脑神经元的运作机制。

1.1.3 第三代神经网络：脉冲神经网络

第三代神经网络，脉冲神经网络 (Spiking Neural Network，SNN) ，旨在弥合神经科学和机器学习之间的差距，使用最拟合生物神经元机制的模型来进行计算，更接近生物神经元机制。脉冲神经网络与目前流行的神经网络和机器学习方法有着根本上的不同。SNN 使用脉冲——这是一种发生在时间点上的离散事件——而非常见的连续值。每个峰值由代表生物过程的微分方程表示出来，其中最重要的是神经元的膜电位。本质上，一旦神经元达到了某一电位，脉冲就会出现，随后达到电位的神经元会被重置。对此，最常见的模型是 Leaky Integrate-And-Fire (LIF) 模型。此外，SNN 通常是稀疏连接的，并会利用特殊的网络拓扑。

📚2 运行结果

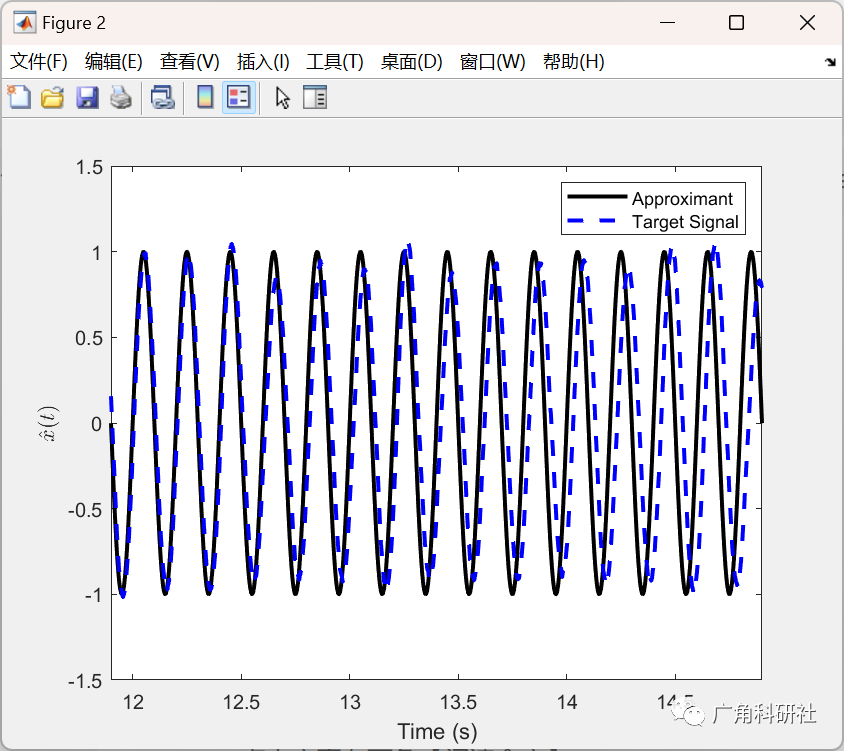
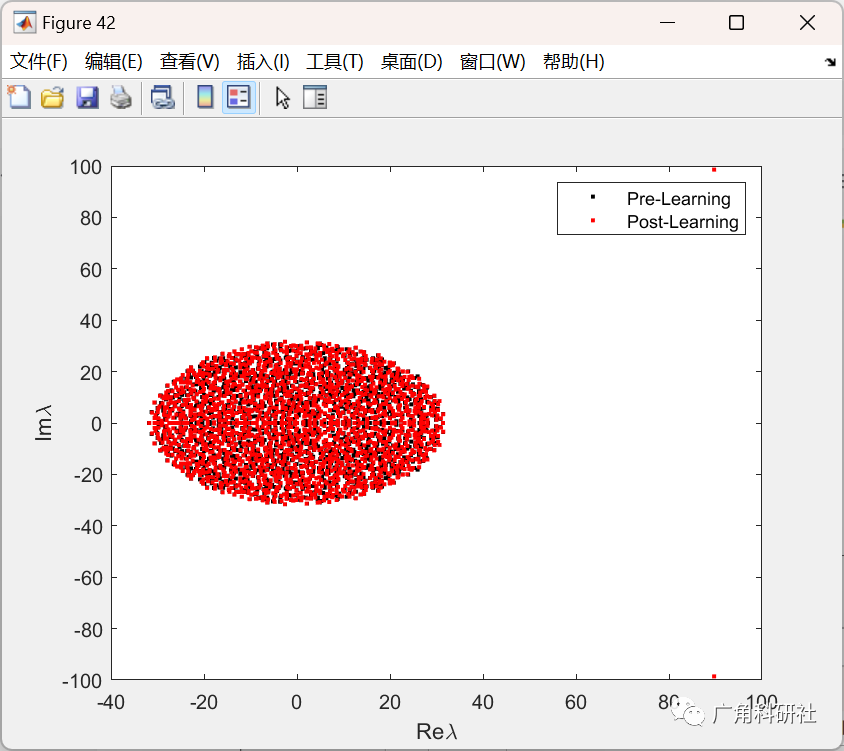
主函数部分代码：

clear allclose allclc%% Fixed parameters across all simulationsdt = 0.00001; %time step N = 2000; %Network Sizetd = 0.02; %decay time tr = 0.002; %Rise time %% T = 15; tmin = 5; tcrit = 10; nt = round(T/dt); tx = (1:1:nt)*dt;  xz = sin(2*tx*pi*5)'; G = 10; Q = 10^4; %% m = min(size(xz)); %dimensionality of teacher E = Q*(2*rand(N,m)-1); %encodersBPhi = zeros(N,m);  %Decoders%% Compute Neuronal Intercepts and Tuning Curves initial = 0;p = 0.1; %Sparse Coupling OMEGA = G*randn(N,N).*(rand(N,N)<p)/(sqrt(N)*p); %Random initial weight matrix %Set the sample row mean of the weight matrix to be 0 to strictly enforce%balance.  for i = 1:1:N     QS = find(abs(OMEGA(i,:))>0);    OMEGA(i,QS) = OMEGA(i,QS) - sum(OMEGA(i,QS))/length(QS);end%% Storage Matrices and Initialization store = 10; %don't store every time step, saves time.  current = zeros(nt,m);  %storage variable for output current IPSC = zeros(N,1); %post synaptic current h = zeros(N,1); r = zeros(N,1); hr = zeros(N,1); JD = 0*IPSC;vpeak = pi; %peak and resetvreset = -pi; v = vreset + (vpeak-vreset)*rand(N,1); %initialze voltage v_ = v; %temporary storage variable for integration j = 1;time = zeros(round(nt/store),1);RECB = zeros(5,round(2*round(nt/store)));REC = zeros(10,round(nt/store));tspike = zeros(8*nt,2);ns = 0;ticSD = 0; BPhi = zeros(N,m);z = zeros(m,1);step = 50; %Sets the frequency of RLS  imin = round(tmin/dt); %Start RLSicrit = round((tcrit/dt)); %Stop RLS  Pinv = eye(N)*dt;  i = 1; %%  ilast = i;  %icrit = ilast;for i = ilast :1:nt JX = IPSC + E*z; %current dv = 1-cos(v) + (1+cos(v)).*JX*(pi)^2;  %dv v = v_ + dt*(dv); %Euler integration plus refractory period.  index = find(v>=vpeak);     if length(index)>0JD = sum(OMEGA(:,index),2); %compute the increase in current due to spiking  tspike(ns+1:ns+length(index),:) = [index,0*index+dt*i];ns = ns + length(index); endif tr == 0     IPSC = IPSC*exp(-dt/td)+   JD*(length(index)>0)/(td);    r = r *exp(-dt/td) + (v>=vpeak)/td;elseIPSC = IPSC*exp(-dt/tr) + h*dt;h = h*exp(-dt/td) + JD*(length(index)>0)/(tr*td);  %Integrate the currentr = r*exp(-dt/tr) + hr*dt; hr = hr*exp(-dt/td) + (v>=vpeak)/(tr*td);endv = v + (vreset - v).*(v>=vpeak); %reset with spike time interpolant implemented.  v_ = v;  %only store stuff every index variable.     z = BPhi'*r;err = z - xz(i,:)';if mod(i,step)==1if i > imin  if i < icrit    cd = Pinv*r;       BPhi = BPhi - (cd*err');   Pinv = Pinv - ((cd)*(cd'))/( 1 + (r')*(cd)); end end end   if mod(i,store) == 1;        j = j + 1; time(j,:) = dt*i;        current(j,:) = z; REC(:,j) = v(1:10); RECB(:,j) = BPhi(1:5,1);    endif mod(i,round(0.1/dt))==1figure(1)drawnow plot(tx(1:1:i),xz(1:1:i,:),'k','LineWidth',2), hold onplot(time(1:1:j),current(1:1:j,:),'b--','LineWidth',2), hold offxlim([dt*i-1,dt*i])xlabel('Time')ylabel('x(t)') figure(2)plot(time(1:1:j),RECB(1:5,1:1:j),'.') xlabel('Time')ylabel('\phi_j') figure(3)plot(tspike(1:1:ns,2), tspike(1:1:ns,1),'k.')ylim([0,100])xlabel('Time')ylabel('Neuron Index')end