一.题目

剑指 Offer 42. 连续子数组的最大和

描述：输入一个整型数组，数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。
要求时间复杂度为O(n)。
示例1:

输入: nums = [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

提示：

• 1 <= arr.length <= 10^5
• -100 <= arr[i] <= 100

二.解题思路分析

1.解析

动态规划是本题的最优解法，以下按照标准流程解题。

2.小结：

 1.状态，即子问题。
dp[i] 代表以元素 nums[i] 为结尾的连续子数组最大和。

2.转移策略，自带剪枝。
若 dp[i−1]≤0 ，说明 dp[i−1] 对 dp[i] 产生负贡献，即 dp[i−1]+nums[i] 还不如 nums[i] 本身大。

3.状态转移方程，根据前两步抽象而来。

当 dp[i−1]>0 时：执行 dp[i] = dp[i-1] + nums[i]；
当 dp[i−1]≤0 时：执行 dp[i] = nums[i] ；
4.设计dp数组，保存子问题的解，避免重复计算

5.实现代码

整个动态规划，最难的就是定义状态。一旦状态定义出来，表明你已经抽象出了子问题，可以肢解原来的大问题了。

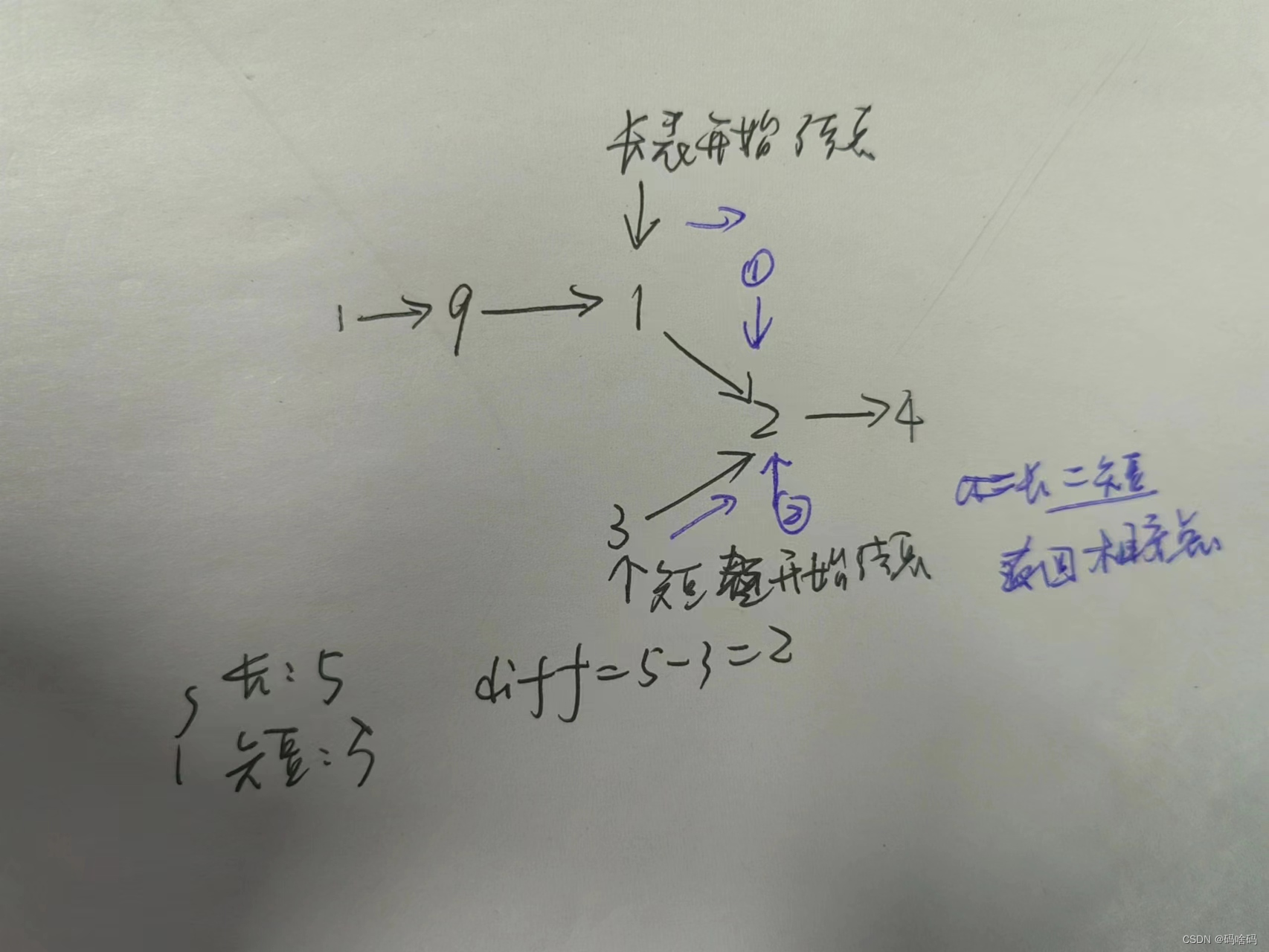
3.附上图解：

三.代码

解法一：

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        for i in range(1, len(nums)):
            nums[i] += max(nums[i - 1], 0)
        return max(nums)

换一种写法：

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        res, cur = nums[0], nums[0]
        for val in nums[1:]:
            cur = max(cur+val, val) # 关键的步骤：cur 要么等于之前之和，要么从当前开始
            res = max(res, cur)
        return res

解法二：

分析：

这个题目其实可以更难一点，例如：让你打印出具有最大连续子数组的和的那个子数组，如果存在多个这样的子数组，把最左边的那个打印出来。
因为我们发现，有很多学生只会求出最大连续子数组的和，但是找不出那个子数组，这就很麻烦，只知其一，不知其二。
要想彻底理解这个题目的动态规划，就应该知道整个结果的转移过程，并且分析清楚。

实际上，就是额外加了一个idx变量，用来记录以第i个元素结尾的最大连续和的子数组的起始下标。

idx是一个动态维护的变量，当发现前一个dp值小于等于0的时候，就应该刷新这个idx，因为将第i个元素拼接上去不会使得这个子数组是最大的，因此我们也没必要再维护这个子数组的起始下标。

反之，我们维持这个idx，不会被i改变，这是因为可以拼接上去，我们要记录下这个子数组的起始。

随后，发现以i元素结尾的dp值比全局res更大，那么就更新全局的起始和终止下标。
不难发现，通过维护起始和终止下标我们就可以知道最大的，但维护res可以记录结果，避免反复计算子数组的和。

最后，就可以知道输出的子数组区间的起始和终止下标。

class Solution(object):
    def maxSubArray(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        curMax = nums[0]
        res = nums[0]
        # 记录起始和结尾idx
        start = 0
        end = 0
        # 当前起始idx
        curStart = 0
        for i in range(1, len(nums)):
            if curMax > 0:
                # dp[i-1]>0时,dp[i]=dp[i-1]+nums[i],当前起始idx不变,和dp[i-1]一样
                curMax = curMax + nums[i]
            else:
                # dp[i-1]<=0时,dp[i]=nums[i],当前起始值变为i
                curStart = i
                curMax = nums[i]

            if curMax >= res:
                # 当max值改变时更新起始值和结尾值
                res = max(curMax, res)
                start = curStart
                end = i
        # 输出最大区间的idx
        print(start, end)
        return res