题目

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/n-queens

示例1

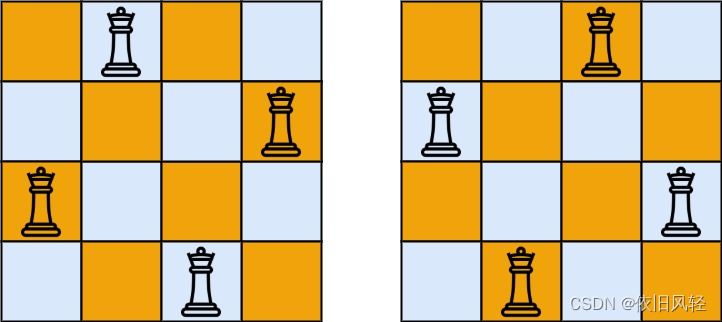
输入：n = 4
输出：[[“.Q…”,“…Q”,“Q…”,“…Q.”],[“…Q.”,“Q…”,“…Q”,“.Q…”]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例2

输入：n = 1
输出：[[“Q”]]

提示

1 <= n <= 9

Show The Swift Code

class Solution {
    func solveNQueens(_ n: Int) -> [[String]] {
        var solutions = [[String]]()
        var queens: [Int] = Array(repeating: -1, count: n)
        var columns = Set<Int>()
        var diagonals1 = Set<Int>()
        var diagonals2 = Set<Int>()
        backtrack(solutions: &solutions, queens: &queens, n: n, row: 0, columns: &columns, diagonals1: &diagonals1, diagonals2: &diagonals2)
        return solutions
    }
    
    private final func backtrack(solutions: inout [[String]], queens: inout [Int], n: Int, row: Int, columns: inout Set<Int>, diagonals1: inout Set<Int>, diagonals2: inout Set<Int>) {
        guard row != n else {
            let board: [String] = generateBoard(queens, n)
            solutions.append(board)
            return
        }
        for col in 0..<n {
            if columns.contains(col) {
                continue
            }
            let diag1 = row - col
            if diagonals1.contains(diag1) {
                continue
            }
            let diag2 = row + col
            if diagonals2.contains(diag2) {
                continue
            }
            queens[row] = col
            columns.insert(col)
            diagonals1.insert(diag1)
            diagonals2.insert(diag2)
            backtrack(solutions: &solutions, queens: &queens, n: n, row: row + 1, columns: &columns, diagonals1: &diagonals1, diagonals2: &diagonals2)
            queens[row] = -1
            columns.remove(col)
            diagonals1.remove(diag1)
            diagonals2.remove(diag2)
        }
    }
    
    private final func generateBoard(_ queens: [Int], _ n: Int) -> [String] {
        var board = [String]()
        for columnIntValue in queens {
            var rowDisplay: [Character] = Array(repeating: ".", count: n)
            rowDisplay[columnIntValue] = "Q"
            board.append(String(rowDisplay))
        }
        return board
    }
}