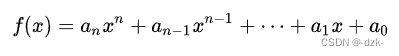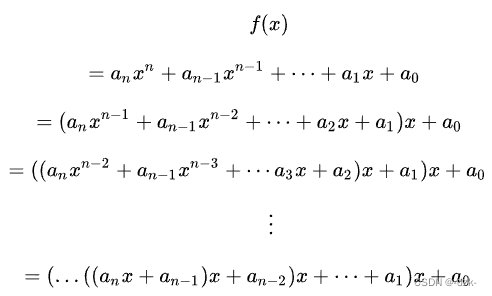一、题目

1、原题链接

2058. 笨拙的手指

2、题目描述

奶牛贝茜正在学习如何在不同进制之间转换数字。

但是她总是犯错误，因为她无法轻易的用两个前蹄握住笔。

每当贝茜将数字转换为一个新的进制并写下结果时，她总是将其中的某一位数字写错。

例如，如果她将数字 14 转换为二进制数，那么正确的结果应为 1110，但她可能会写下 0110 或 1111 。

贝茜不会额外添加或删除数字，但是可能会由于写错数字的原因，写下包含前导 0 的数字。

给定贝茜将数字 N 转换为二进制数字以及三进制数字的结果，请 确定 N 的正确初始值（十进制表示）。

输入格式

第一行包含 N 的二进制表示，其中一位是错误的。

第二行包含 N 的三进制表示，其中一位是错误的。

输出格式

输出正确的 N 的值。

数据范围

0≤N≤10⁹，且存在唯一解。

输入样例：
1010
212
输出样例：
14
样例解释
14 在二进制下的正确表示为 1110，在三进制下的正确表示为 112。

二、解题报告

1、思路分析

思路来源：y总视频讲解
y总yyds

（1）将数N的二进制表示下可能写错的每种情况的十进制下的数值存入哈希表中。
（2）将数N的三进制表示下的每种写错的情况的十进制下的数值在哈希表中进行查找，如果该数值出现过，则该数就是N的十进制表示，输出即可。

2、时间复杂度

时间复杂度为O(n)

3、代码详解

使用STL中unordered_set

#include <iostream>
#include <string>
#include <unordered_set>
using namespace std;
//使用秦九韶算法，将y进制下的数x转化为十进制
int ten(string x,int y){
    int ans=0;
    for(int i=0;i<x.size();i++){
        ans=ans*y+x[i]-'0';
    }
    return ans;
}
int main(){
    string n,m;
    cin>>n>>m;
    unordered_set<int> s;
    for(int i=0;i<n.size();i++){
        string t=n;
        t[i]^=1;      //改变第i位数，0变1,1变0
        if(t[0]=='0'&&t.size()>1) continue;   //如果数字存在前导0，则不合法，直接跳过
        s.insert(ten(t,2));             //将写错后的数字在十进制下的数值放入哈希表
    }
    for(int i=0;i<m.size();i++){
        for(int j=0;j<3;j++){       //枚举第i位数字可能的写错情况，然后再在哈希表中查找该数的十进制下数值是否出现过
            if(m[i]-'0'!=j){       
                string tmp=m;
                tmp[i]=j+'0';
                if(tmp[0]=='0'&&tmp.size()>1) continue;   //同上
                if(s.count(ten(tmp,3))){       //如果该数的十进制的值在哈希表存在过，直接输出，该数就是答案
                    cout<<ten(tmp,3);
                }
            }
        }
    }
    return 0;
}

手写哈希表

#include <iostream>
#include <string>
#include <cstring>
using namespace std;
const int N=103;
int h[N];
//哈希表开放寻址法，如果x存在，返回x的位置，否则返回x应该插入的位置
int find(int x){
    int t=(x%N+N)%N;
    while(h[t]!=-1&&h[t]!=x){
        t++;
        if(t==N) t=0;
    }
    return t;
}
//使用秦九韶算法，将y进制下的数x转化为十进制
int ten(string x,int y){
    int ans=0;
    for(int i=0;i<x.size();i++){
        ans=ans*y+x[i]-'0';
    }
    return ans;
}

int main(){
    string n,m;
    cin>>n>>m;
    memset(h,-1,sizeof h);
    for(int i=0;i<n.size();i++){
        string t=n;
        t[i]^=1;      //改变第i位数，0变1,1变0
        if(t[0]=='0'&&t.size()>1) continue;   //如果数字存在前导0，则不合法，直接跳过
        h[find(ten(t,2))]=ten(t,2);             //将写错后的数字在十进制下的数值放入哈希表
    }
    for(int i=0;i<m.size();i++){
        for(int j=0;j<3;j++){       //枚举第i位数字可能的写错情况，然后再在哈希表中查找该数的十进制下数值是否出现过
            if(m[i]-'0'!=j){       
                string tmp=m;
                tmp[i]=j+'0';
                if(tmp[0]=='0'&&tmp.size()>1) continue;   //同上
                if(h[find(ten(tmp,3))]!=-1){       //如果该数的十进制的值在哈希表存在过，直接输出，该数就是答案
                    cout<<ten(tmp,3);
                }
            }
        }
    }
    return 0;
}

三、知识风暴

哈希表

哈希表的增删改查的时间复杂度为O(1)。
C++中STL的unordered_set和unordered_map底层就是使用哈希结构实现的。

秦九韶算法

参考百度百科
秦九韶算法是一种多项式的简化算法。
具体做法是将多项式
改写为：
先计算内层的数值然后依次由内向外进行拓展。
针对本题我们可以使用其来进行计算不同进制转十进制的结果。
例如：求二进制1010的十进制
二进制1010转换为10进制的算式可以写成1x2³+0x2²+1x2¹+0x2⁰,类比上述多项式，2即为多项式中的x，二进制的每位数字则是多项式的系数，而我们在本题中二进制数是按字符串（记为s）读入的，所以将其每位数字记为s[i]。根据上述算法可知，我们最终算的每层均是s[i]*x+s[i+1]，而在计算下一层时，上一层的结果更新成了下一层x前面的系数，所以我们将上一层的结果记录到临时变量ans中，然后按照公式s[i]*x+s[i+1]依次向外扩展，直到遍历完所有数字，ans就是多项式的值，也就是我们要求的十进制的数值。

所以据此我们可以总结出计算本题将x进制转换为十进制数值的代码
int ans=0;     //ans存储每层的结果，最终ans的值为最外层的值，也就是多项式的值
for(int i=0;i<s.size();i++){
    ans=ans*x+s[i]-'0';      //i可以理解为层数，第0层只有第一个数字，而最后一层就是整个多项式的值
}