一、背包问题概述:
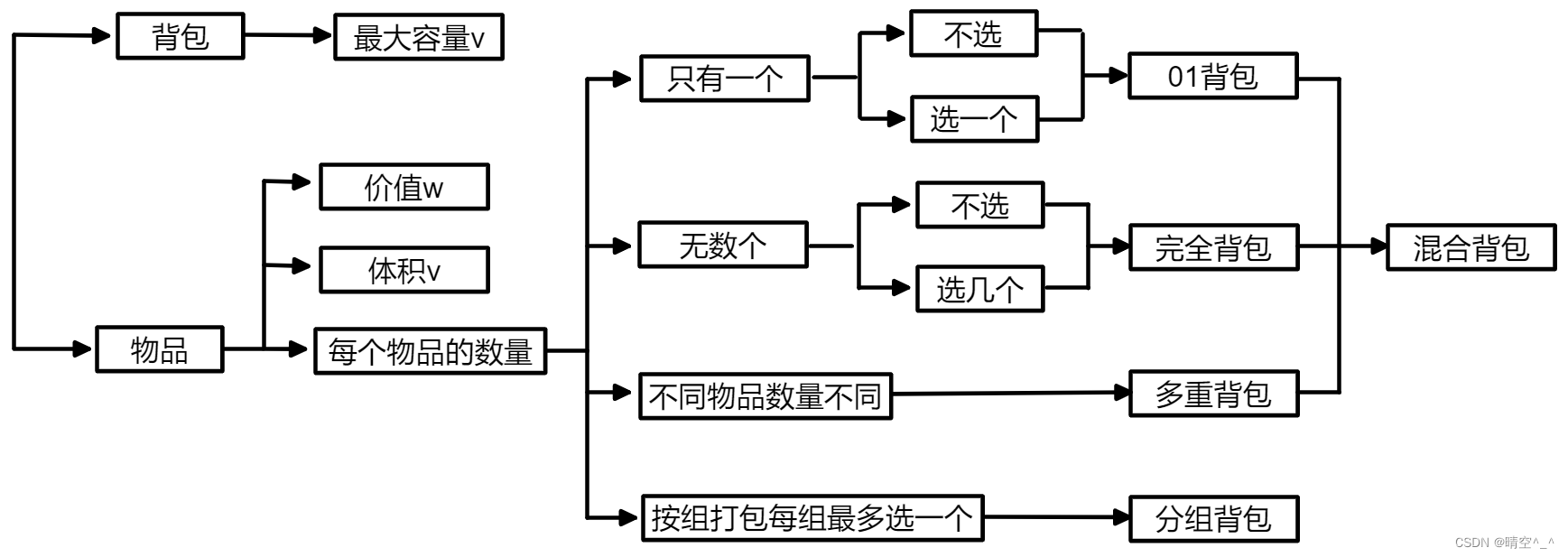
二、暴力解法:
| 重量 | 价值 | |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
背包最大容量为4。
每一个物品有两个状态,“取”或者“不取”。利用回溯法可以暴力枚举所有物品的状态的排列组合状态,与背包最大容量比较就可以求得最大的价值,时间复杂是 O ( 2 n ) O(2^n) O(2n)为指数级别,故需要动态规划的解法来进行优化。
三、二维DP数组解01背包
1.DP数组含义
dp[i][j]:任取编号为[0,i]内的物品,放到容量为j的背包内所得到的最大价值。
2.递推公式(对dp[i][j])
- 不放物品
i:dp[i][j]=dp[i-1][j] - 放物品
i:dp[i][j]=dp[i-1][j-weight[i]] + value[i]
dp[i][j]最终应该取放物品i和不放物品i中大的那一个值。
故,dp[i][j]=max(dp[i-1][j], dp[i-1][j-weight[i]]+value[i])
3.DP数组解析

如图,对于dp[i][j](红色表格),其取值由两个方向得到:
dp[i][j]=dp[i-1][j],由1号红色箭头得到;dp[i][j]=dp[i-1][j-weight[i]] + value[i],由2号箭头得到。具体2号箭头的初始位置则由weight[i]决定。
所以,求解DP数组时[i-1]必须是已知的,故DP数组初始化时第一行必须初始化。
第一列不需要初始化,使用if判断j-weight[i] > 0 即可。
综上,初始化时,只初始化第一行,其余位置皆不用初始化。
就本题而言,初始化数组为:

4.遍历顺序
i先遍历物品再遍历背包

本方法本质是按行遍历,对每个物品从容量0到j逐个测试。由DP数组解析可得,求dp[i][j]时必须知道dp[i-1][0~j]内的所有数据,而这在前一次循环中已经得到。故该遍历方法可行。
ii先遍历背包再遍历物品
 本方法本质是按列遍历,对每个容量从物品
本方法本质是按列遍历,对每个容量从物品0到i逐个测试。由DP数组解析可得,求dp[i][j]时必须知道dp[i-1][0~j]内的所有数据,而这在前一次循环中已经得到。故该遍历方法可行。
5. 代码:
void knapsack () {
vector<int> weight = {1, 3, 4}; // 物品重量
vector<int> value = {15, 20, 30}; // 物品价值
int bagweight = 4; // 背包的最大容量
// 创建二维数组
vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
// 初始化
for (int j = weight[0]; j <= bagweight; j++) {
dp[0][j] = value[0];
}
// 先遍历物品
for(int i = 1; i < weight.size(); i++) { // 遍历物品
for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
// 先遍历背包
// for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
// for(int i = 1; i < weight.size(); i++) { // 遍历物品
// if (j < weight[i]) dp[i][j] = dp[i - 1][j];
// else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
// }
// }
cout << dp[weight.size() - 1][bagweight] << endl;
}
四、一维DP数组(滚动数组)解01背包
1.DP数组含义
从二维DP数组的遍历图中可以看出求解dp[i][j]完全是在使用DP数组的前一行(或前一列)的数据,且对dp[i][j]后面的内容完全不关心。因此,可以考虑将前一行(或前一列)的数据覆盖到当前行,使用一行(或一列)就可以完成计算,这就是本题一维DP数组的思想。
本题定义dp[j]为容量为j的背包能装物品的最大价值(相当于将二维数组压缩为一行)。
2.递推公式
- 不放物品
i:dp[j]=dp[j](可以将等号后dp[j]的看作上一行的数据,只是覆盖到了当前行) - 放物品
i:dp[j]=dp[j-weight[i]]+value[i](可以将等号后的dp[j-weight[i]]看作上一行的数据,只是覆盖到了当前行)
dp[j]=max(dp[j], dp[j-weight[i]]+value[i])
3.DP数组初始化
由数组的定义可知,求dp[j]只需知道其前面的数据即可。考虑一下,最“前面”的数据就是背包不放任何物体。故将DP数组所有元素设置为0即可。
4.遍历顺序
因为当前DP数组的值可以看成为上一行的覆盖,故为了保持dp[j]前的元素的“干净”,遍历j时应该采用倒叙遍历。

如图,蓝色代表当前行已经更新的值,红色代表当前行正要求的值,绿色代表上一行还没有更新的值。从后往前遍历可以保证对dp[j]更新时,其前面的值都不会被改变。如果采用正序遍历,相当于dp[j]前的值为当前行的值(这种说法也不对,物品i的值被累加了),递推公式就不成立了。
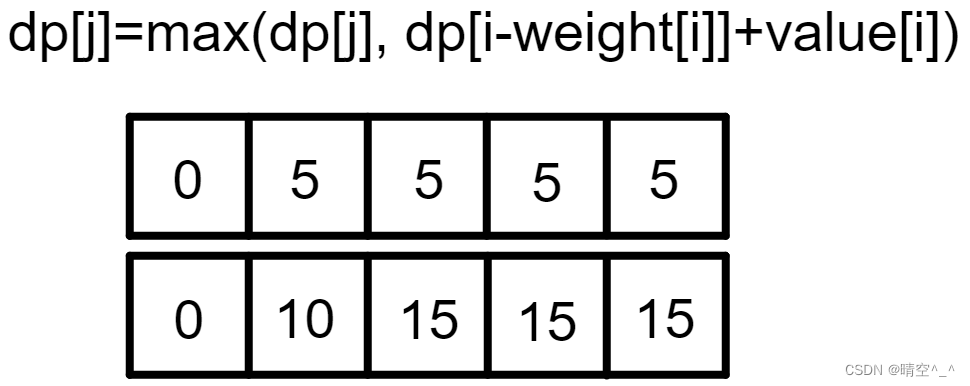
假设物品重量{1, 1},价值{5, 10},背包最大容量为4。如图,若采用正序遍历

在第二行更新DP时,由于dp[j]前的数据已经被污染,故每次更新dp[j]时都对物品1的价值进行了累加。而倒叙时由于前面数据没有被污染,则不会产生累加的错误。如图:
5.代码
void test_1_wei_bag_problem() {
vector<int> weight = {1, 3, 4};
vector<int> value = {15, 20, 30};
int bagWeight = 4;
// 初始化
vector<int> dp(bagWeight + 1, 0);
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
cout << dp[bagWeight] << endl;
}