1.最小的K个数
sort直接用太无脑了,虽然底层实现也是快排,但是快排还是得会写啊
快速排序
快速排序算法有两个核心点,分别为 “哨兵划分” 和 “递归” 。
哨兵划分操作: 以数组某个元素(一般选取首元素)为 基准数 ,将所有小于基准数的元素移动至其左边,大于基准数的元素移动至其右边。

class Solution {
public:
void quickSort(vector<int>&arr,int l,int r){
//如果数组长度为1时停止
if(l>=r) return;
int i=l,j=r;
while(i<j)
{
while(i<j&&arr[j]>=arr[l]) j--;
while(i<j&&arr[i]<=arr[l]) i++;
swap(arr[i],arr[j]);
}
swap(arr[l],arr[i]);
quickSort(arr,l,i-1);
quickSort(arr,i+1,r);
}
vector<int> getLeastNumbers(vector<int>& arr, int k) {
quickSort(arr,0,arr.size()-1);
vector<int> res;
res.assign(arr.begin(),arr.begin()+k);
return res;
}
};2.数据流中的中位数
双优先队列
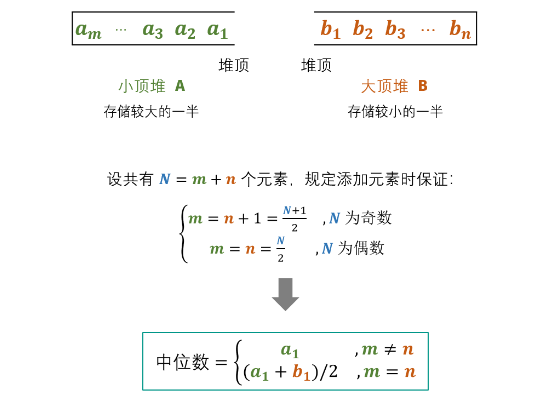
优先队列和queue不同的就在于我们可以自定义其中数据的优先级, 让优先级高的排在队列前面,优先出队
优先队列具有队列的所有特性,包括基本操作,只是在这基础上添加了内部的一个排序,它本质是一个堆实现的
和队列基本操作相同:
top 访问队头元素
empty 队列是否为空
size 返回队列内元素个数
push 插入元素到队尾 (并排序)
emplace 原地构造一个元素并插入队列
pop 弹出队头元素
swap 交换内容
定义:priority_queue<Type, Container, Functional>
Type 就是数据类型,Container 就是容器类型(Container必须是用数组实现的容器,比如vector,deque等等,但不能用 list。STL里面默认用的是vector),Functional 就是比较的方式,当需要用自定义的数据类型时才需要传入这三个参数,使用基本数据类型时,只需要传入数据类型,默认是大顶堆
//升序队列
priority_queue <int,vector<int>,greater<int> > q;
//降序队列
priority_queue <int,vector<int>,less<int> >q;
//greater和less是std实现的两个仿函数(就是使一个类的使用看上去像一个函数。其实现就是类中实现一个operator(),这个类就有了类似函数的行为,就是一个仿函数类了)#include<iostream>
#include <queue>
using namespace std;
int main()
{
//对于基础类型 默认是大顶堆
priority_queue<int> a;
//等同于 priority_queue<int, vector<int>, less<int> > a;
priority_queue<int, vector<int>, greater<int> > c; //这样就是小顶堆
priority_queue<string> b;
for (int i = 0; i < 5; i++)
{
a.push(i);
c.push(i);
}
while (!a.empty())
{
cout << a.top() << ' ';
a.pop();
}
cout << endl;
while (!c.empty())
{
cout << c.top() << ' ';
c.pop();
}
cout << endl;
b.push("abc");
b.push("abcd");
b.push("cbd");
while (!b.empty())
{
cout << b.top() << ' ';
b.pop();
}
cout << endl;
return 0;
}
输出:
4 3 2 1 0
0 1 2 3 4
cbd abcd abcclass MedianFinder {
private:
priority_queue<int,vector<int>,less<int>> queMin;//大顶堆--存放较小的值
priority_queue<int,vector<int>,greater<int>> queMax;//小顶堆--存放较大的值
public:
/** initialize your data structure here. */
MedianFinder() {
}
void addNum(int num) {
if(queMin.size()==queMax.size())
{
//如果两个队列里元素数量相同,优先往小顶堆里加
queMax.push(num);
int top=queMax.top();
queMax.pop();
queMin.push(top);
}
else
{
//如果元素的数量不同,往大顶堆里加
queMin.push(num);
int top=queMin.top();
queMin.pop();
queMax.push(top);
}
}
double findMedian() {
if(queMax.size()==queMin.size()) return (queMax.top()+queMin.top())/2.0;
//右边数量一直是大于等于左边的
else return queMin.top();
}
};