一、提出背景
当前一阶的物体检测算法,如SSD和YOLO等虽然实现了实时的速度,但精度始终无法与两阶的Faster RCNN相比。是什么阻碍了一阶算法的高精度呢?何凯明等人将其归咎于正、负样本的不平衡,并基于此提出了新的损失函数Focal Loss及网络结构RetinaNet,在与同期一阶网络速度相同的前提下,其检测精度比同期最优的二阶网络还要高。
为了解决一阶网络中样本的不均衡问题,何凯明等人首先改善了分类过程中的交叉熵函数,提出了可以动态调整权重的Focal Loss。
二、交叉熵损失
1. 标准交叉熵损失
标准的交叉熵函数,其形式如式(2-1)所示:
C
E
(
p
,
y
)
=
{
−
l
o
g
(
p
)
i
f
(
y
=
1
)
−
l
o
g
(
1
−
p
)
o
t
h
e
r
w
i
s
e
(2-1)
CE(p,y)=\left\{\begin{matrix} -log(p) & if(y=1) & \\ -log(1-p) & otherwise & \end{matrix}\right.\tag{2-1}
CE(p,y)={−log(p)−log(1−p)if(y=1)otherwise(2-1)
公式中,
p
p
p代表样本在该类别的预测概率,
y
y
y代表样本标签。可以看出,当标签为1时,
p
p
p越接近1,则损失越小;标签为0时,
p
p
p越接近0,则损失越小,符合优化的方向。
为了方便表示,按照式(2-2)将
p
p
p标记为
p
t
p_{t}
pt:
p
t
=
{
p
i
f
(
y
=
1
)
1
−
p
o
t
h
e
r
w
i
s
e
(2-2)
p_{t}=\left\{\begin{matrix} p & if(y=1) & \\ 1-p & otherwise & \end{matrix}\right.\tag{2-2}
pt={p1−pif(y=1)otherwise(2-2)
则交叉熵可以表示为式(2-3)的形式:
C
E
(
p
,
y
)
=
C
E
(
p
i
)
=
−
l
o
g
(
p
i
)
(2-3)
CE(p,y)=CE(p_{i})=-log(p_{i})\tag{2-3}
CE(p,y)=CE(pi)=−log(pi)(2-3)
标准的交叉熵中所有样本的权重都是相同的,因此如果正、负样本不均衡,大量简单的负样本会占据主导地位,少量的难样本与正样本会起不到作用,导致精度变差。
2. 平衡交叉熵损失
为了改善样本的不平衡问题,平衡交叉熵在标准的基础上增加了一个系数 α t \alpha _{t} αt来平衡正、负样本的权重, α t \alpha _{t} αt由超参数 α \alpha α按照式(2-4)计算得来, α \alpha α取值在[0,1]区间内。
α t = { α i f ( y = 1 ) 1 − α o t h e r w i s e (2-4) \alpha _{t}=\left\{\begin{matrix} \alpha & if(y=1) & \\ 1-\alpha & otherwise & \end{matrix}\right.\tag{2-4} αt={α1−αif(y=1)otherwise(2-4)
有了 α t \alpha _{t} αt,平衡交叉熵损失公式如式(2-5)所示:
C E ( p t ) = − α t l o g ( p t ) (2-5) CE(p_{t})=-\alpha _{t}log(p_{t})\tag{2-5} CE(pt)=−αtlog(pt)(2-5)
尽管平衡交叉熵损失改善了正、负样本间的不平衡,但由于其缺乏对难易样本的区分,因此没有办法控制难易样本之间的不均衡。
三、Focal Loss
Focal Loss为了同时调节正、负样本与难易样本,提出了如式(3-1)所示的损失函数:
F L ( p t ) = − α t ( 1 − p t ) γ l o g ( p t ) (3-1) FL(p_{t})=-\alpha_{t}(1-p_{t})^{\gamma}log(p_{t})\tag{3-1} FL(pt)=−αt(1−pt)γlog(pt)(3-1)
对于该损失函数,又如下3个属性:
- 与平衡交叉熵类似,引入了 α t \alpha_{t} αt权重,为了改善正负样本的不均衡,可以提升一些精度。
- ( 1 − p t ) γ (1-p_{t})^{\gamma} (1−pt)γ是为了调节难易样本的权重。当一个边框被误分类时, p t p_{t} pt较小,则 ( 1 − p t ) γ (1-p_{t})^{\gamma} (1−pt)γ接近于1,其损失几乎不受影响;当 p t p_{t} pt接近于1时,表明其分类预测较好,是简单样本, ( 1 − p t ) γ (1-p_{t})^{\gamma} (1−pt)γ接近于0,因此其损失被调低了。
- γ \gamma γ是一个调制因子, γ \gamma γ越大,简单样本损失的贡献度会越低,
四、RetinaNet
为了验证Focal Loss的效果,何凯明等人还提出了一个一阶物体检测结构RetinaNet,其结构如图4-1所示:
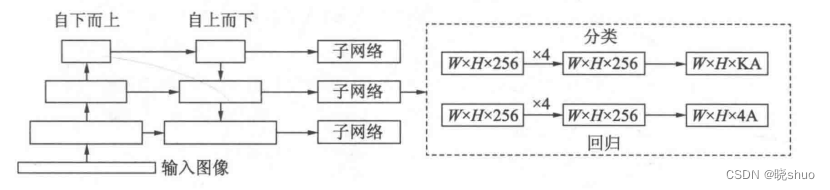
- 在Backbone部分,RetinaNet利用ResNet与FPN构建了一个多尺度特征的特征金字塔。
- RetinaNet使用了类似于Anchor的预选框,在每一个金字塔层,使用了9个大小不同的预选框。
- 分类子网络:分类子网络为每一个预选框预测其类别,因此其输出特征大小为KA×W×H,A默认为9,K代表类别数。中间使用全卷积网络与ReLU激活函数,最后利用Sigmoid函数输出预测值。
- 回归子网络:回归子网络与分类子网络平行,预测每一个预测框的偏移量,最终输出特征的大小为4A×W×W。与当前主流工作不同的是,两个子网络没有权重的共享。


![Melis4.0[D1s]:2.启动流程(GUI桌面加载部分)跟踪笔记](https://img-blog.csdnimg.cn/d389a0cf179f48b1a6cb5f951a9b19e4.png)
