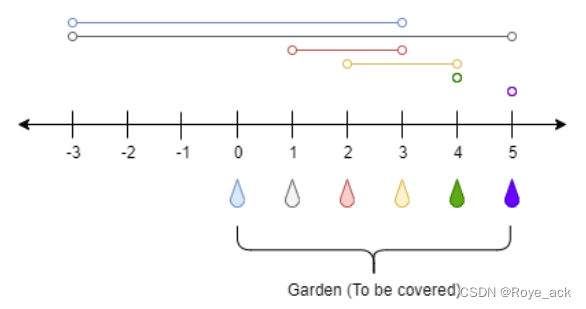
GBDT(Gradient Boosting Decision Tree)在数据分析和预测中的效果很好。它是一种基于决策树的集成算法。其中Gradient Boosting 是集成方法boosting中的一种算法,通过梯度下降来对新的学习器进行迭代。而GBDT中采用的就是CART决策树
一、Boosting
Boosting指把多个弱学习器相加,产生一个新的强学习器(如adaboost, GBDT, xgboost)。每一个弱学习器表示为
f
i
(
x
)
f_{i}(x)
fi(x),则Boost强学习器为
F
(
x
)
=
∑
f
i
(
x
)
F(x)=\sum{f_{i}(x)}
F(x)=∑fi(x)
Boosting是把多个学习器串联,bagging是把多个学习器并联。
二、Gradient Boosting
对于输入 x x x和结果 y y y。
第一个学习器预测出 f 1 ( x ) = y ′ f_{1}(x)=y' f1(x)=y′,则残差 β = y − y ′ β=y-y' β=y−y′,此时将 β β β看作下一个学习器 f 2 ( x ) f_{2}(x) f2(x)的训练目标。
即对于n-1个弱学习器组成的强学习器
F
n
−
1
(
x
)
=
∑
i
=
1
n
−
1
f
i
(
x
)
F_{n-1}(x)=\sum_{i=1}^{n-1}{f_{i}(x)}
Fn−1(x)=i=1∑n−1fi(x)
下一个弱学习器
f
n
(
x
)
f_{n}(x)
fn(x)将
y
−
F
n
−
1
(
x
)
y-F_{n-1}(x)
y−Fn−1(x)作为新的学习目标进行学习。

而GBDT则是把CART决策树作为每次弱分类器学习的方法。
三、优势和缺陷
1、优点
- 各弱学习器层数较浅,训练难度小
- 能处理非线性数据。可以灵活处理各种类型的数据,包括连续值和离散值。
- 使用一些健壮的损失函数,对异常值的鲁棒性非常强。比如 Huber损失函数和Quantile损失函数。
2、缺点
- 由于弱学习器之间存在依赖关系,难以并行训练数据。不过可以通过自采样的SGBT来达到部分并行。
- 适合低维数据,如果数据维度较高时会加大算法的计算复杂度
参考链接:
GBDT算法介绍
GBDT算法的优缺点


![buu [BJDCTF2020]signin 1](https://img-blog.csdnimg.cn/4a19b6d279d74e9c9c2acdda469e70a6.png)