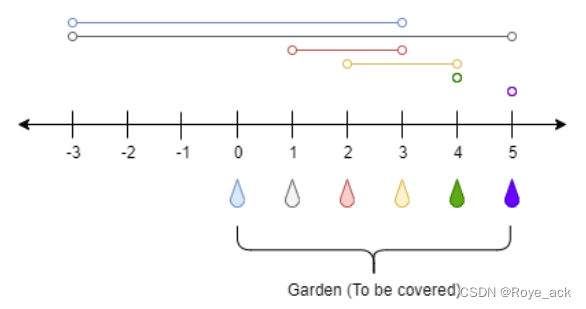
1326. 灌溉花园的最少水龙头数目 

题目：

思路：

注意：「整个花园」包含不是整点的位置，例如 0.5 这种小数位置也要被灌溉到

对于所有能覆盖某个左端点的水龙头，选择能覆盖到最远右端点的水龙头是最优解

比较像【搭桥】的过程，当你走到桥尾，选择一个能搭上且能到达最远的桥

先预处理：第i个水龙头能覆盖的左端点max(0,i-ranges[i])，右端点min(n,i+ranges[i])

设maxright[i]表示能覆盖左端点i的最远右端点值

eg:maxright[0]=5 表示能覆盖0的水龙头，且最远右端点能达到5

curmax表示当前能覆盖的最远右端点

pre表示上一个水龙头能覆盖的最远右端点

在 [0,...n-1] 的范围内遍历所有位置，对于当前位置 i，用maxright[i]更新curmax

• 如果 curmax≤i，说明无法覆盖下一个位置，返回 -1。
• 如果 pre=i，说明需要使用一个新的子区间，因此res++，并且更新 pre=curmax

class Solution {
    public int minTaps(int n, int[] ranges) {
        int[] maxright=new int[n+1];
        //maxright[i]表示能覆盖左端点i的水龙头中，最大的右端点
        for(int i=0;i<=n;i++)
        {
            int l=Math.max(0,i-ranges[i]),r=Math.min(n,i+ranges[i]);
            maxright[l]=Math.max(maxright[l],r);
        }

        int res=0,curmax=0,pre=0;
        //curmax表示当前能覆盖的最远右端点
        //pre表示上一个水龙头能覆盖的最远右端点
        for(int i=0;i<n;i++) //从位置i走到下一个位置，位置n不需要走到下一个位置，所以遍历到n-1
        {
            curmax=Math.max(curmax,maxright[i]);
            if(curmax<=i) return -1;
            if(pre==i)
            {
                res++;
                pre=curmax;
            }
        }
        return res;
    }
}