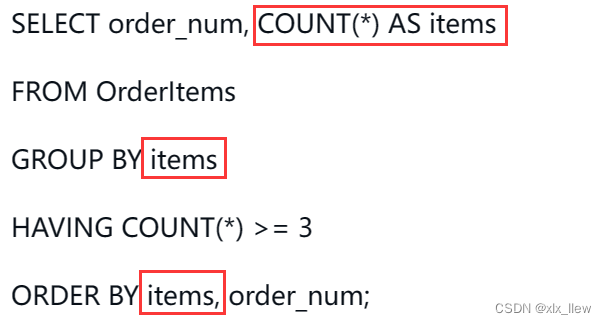
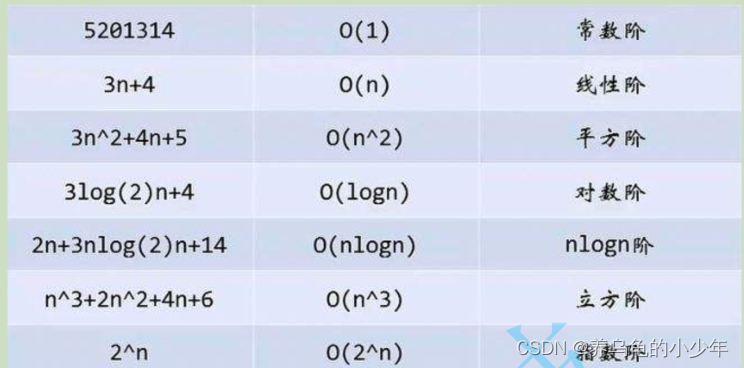
目录

一。Jensen不等式：若f是凸函数

二。最大似然估计 

三。二项分布的最大似然估计

四。进一步考察 

1.按照MLE的过程分析 

2.化简对数似然函数 

3.参数估计的结论 

4.符合直观想象

五。从直观理解猜测GMM的参数估计 

1.问题：随机变量无法直接(完全)观察到 

2.从直观理解猜测GMM的参数估计 

3.建立目标函数 

4.第一步：估算数据来自哪个组份 

5.估计每个组份的参数 

六。EM算法的提出  

1.通过最大似然估计建立目标函数

 2.问题的提出​编辑

3.Jensen不等式

4.寻找尽量紧的下界 

5.进一步分析

七。EM算法整体框架 

八。从理论公式推导GMM 

1.E-step 

2.M-step 

3.对均值求偏导 

4.高斯分布的均值 

5.高斯分布的方差：求偏导，等于0 

6.多项分布的参数 

7.拉格朗日乘子法 

8.求偏导，等于0 

9.总结

九。pLSA模型 

1.D代表文档，Z代表主题(隐含类别)，W代表单词；

2.最大似然估计：wj在di中出现的次数​编辑 

3.目标函数分析  

4.求隐含变量主题zk的后验概率 

5.分析似然函数期望  

6.关于参数P(zk|di)P(wj|zk) 的似然函数期望 

7.完成目标函数的建立 

8.目标函数的求解 

9.分析第一个等式

10.同理分析第二个等式 

11.pLSA的总结 

12. pLSA进一步思考

---

一。Jensen不等式：若f是凸函数

经典的K-means聚类方法，能够非常方便的将未标记的样本分成若干簇； 
但无法给出某个样本属于该簇的后验概率。

其他方法可否处理未标记样本呢？  

二。最大似然估计 

找出与样本的分布最接近的概率分布模型。简单的例子 
10次抛硬币的结果是：正正反正正正反反正正

假设p是每次抛硬币结果为正的概率。则：得到这样的实验结果的概率是： 

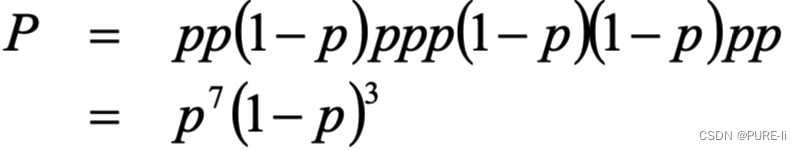
最优解是：p=0.7  

三。二项分布的最大似然估计

投硬币试验中，进行N次独立试验，n次朝上，N-n次朝下。 

假定朝上的概率为p，使用对数似然函数作为目标函数： 

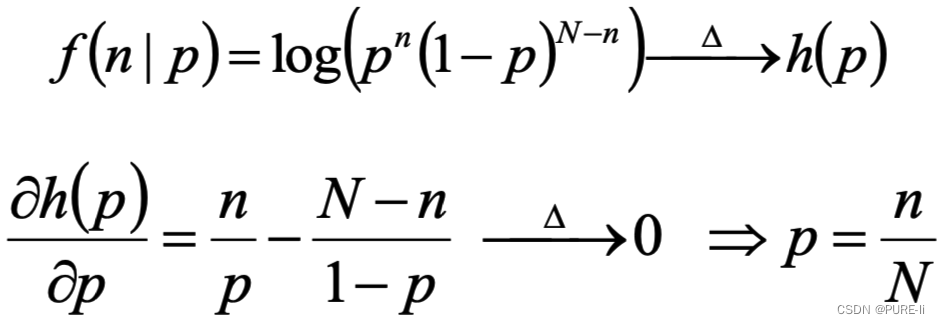
四。进一步考察 

若给定一组样本x1,x2…xn，已知它们来自于高斯分布N(μ,σ)，试估计参数μ,σ。  

1.按照MLE的过程分析 

高斯分布的概率密度函数： 

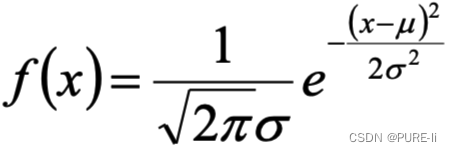
将Xi的样本值xi带入，得到： 

 

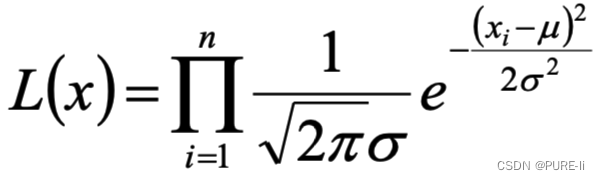
2.化简对数似然函数 

 

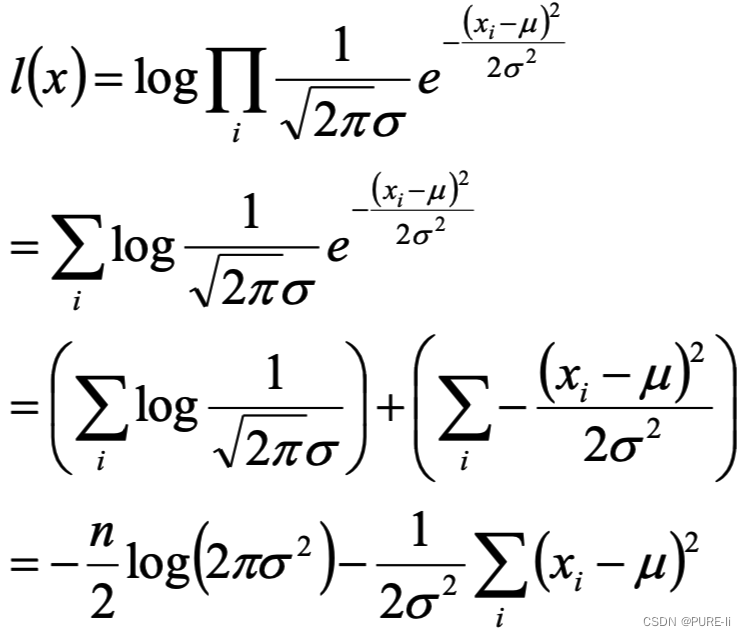
3.参数估计的结论 

 

4.符合直观想象

上述结论和矩估计的结果是一致的，并且意义非常直观：样本的均值即高斯分布的均值，样本的伪方差即高斯分布的方差。  

五。从直观理解猜测GMM的参数估计 

1.问题：随机变量无法直接(完全)观察到 

随机挑选10000位志愿者，测量他们的身高：若样本中存在男性和女性，身高分别服从N(μ1,σ1)和N(μ2,σ2)2)的分布，试估计μ1,σ1,1,μ2,σ2 。

给定一幅图像，将图像的前景背景分开 

无监督分类：聚类/EM 

2.从直观理解猜测GMM的参数估计 

随机变量X是有K个高斯分布混合而成，取各个高斯分布的概率为π1π2... πK，第i个高斯分布的均值为μi，方差为Σi。若观测到随机变量X的一系列样本x1,x2,...,xn，试估计参数π，μ，Σ。 

3.建立目标函数 

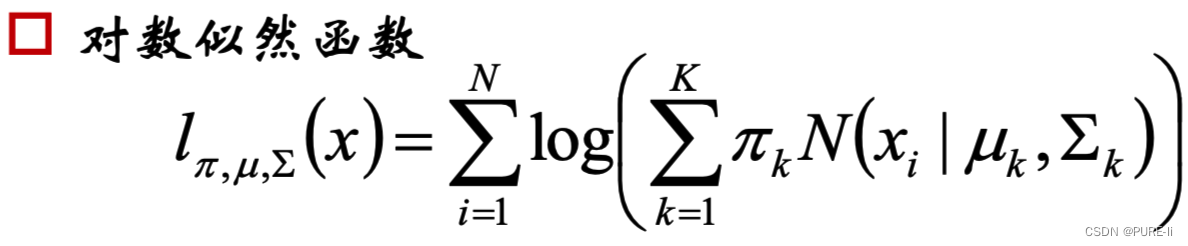
由于在对数函数里面又有加和，无法直接用求导解方程的办法直接求得最大值。为了解决这个问题，我们分成两步。

4.第一步：估算数据来自哪个组份 

估计数据由每个组份生成的概率：对于每个样本xi，它由第k个组份生成的概率为 

 

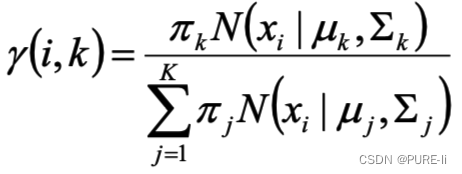
上式中的μ和Σ也是待估计的值，因此采样迭代法：在计算γ(i,k)时假定μ和Σ已知； 

        需要先验给定μ和Σ。 

        γ(i,k) 亦可看成组份k在生成数据xi时所做的贡献。 

5.估计每个组份的参数 

对于所有的样本点，对于组份k而言，可看做生成了 这些点。组份k是一个标准的高斯分布，利用上面的结论：  

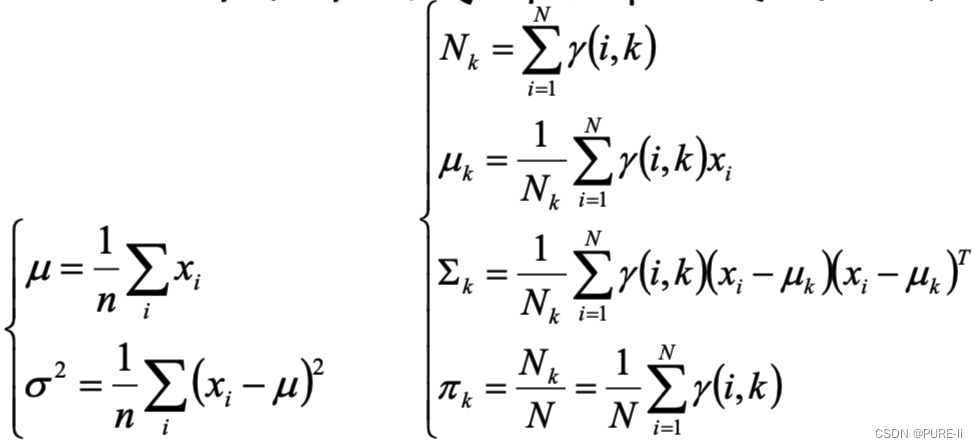
六。EM算法的提出  

假定有训练集  包含m个独立样本，希望从中找到该组数据的模型p(x,z)的参数。

1.通过最大似然估计建立目标函数

取对数似然函数 

 

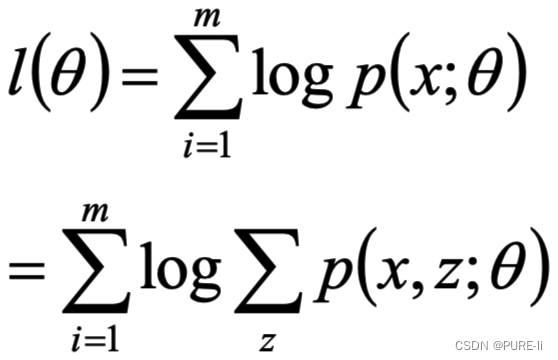
 2.问题的提出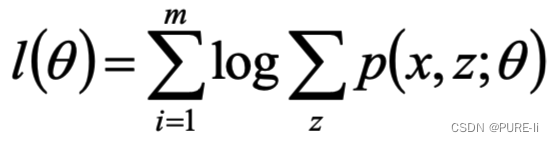

z是隐随机变量，不方便直接找到参数估计。策略：计算l(θ)下界，求该下界的最大值；重复该过程，直到收敛到局部最大值。  

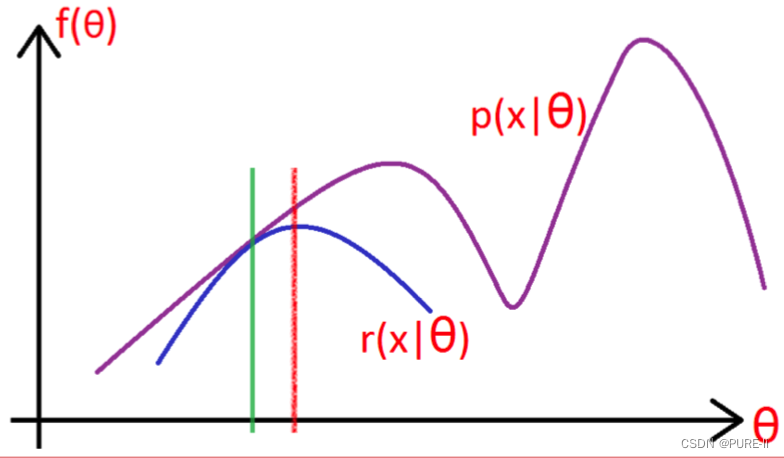
3.Jensen不等式

 

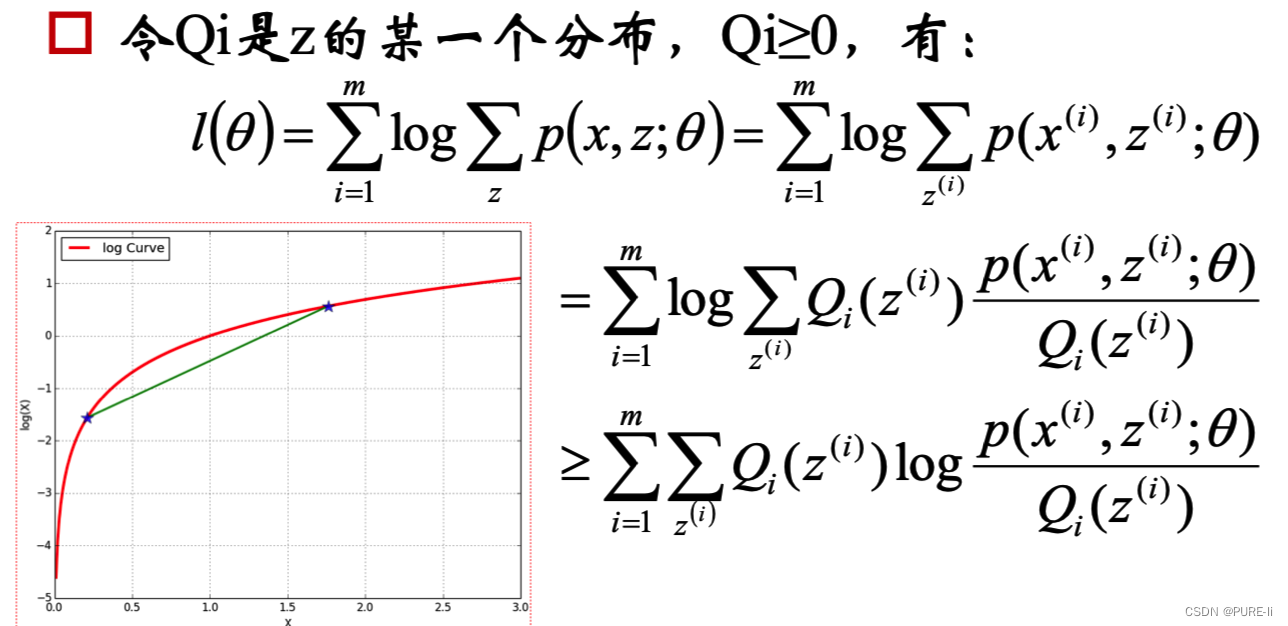
4.寻找尽量紧的下界 

为了使等号成立 

 

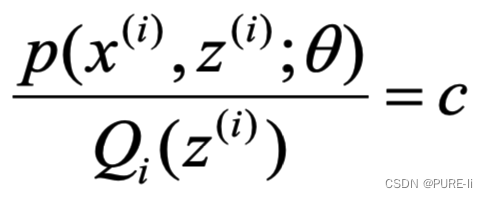
5.进一步分析

 

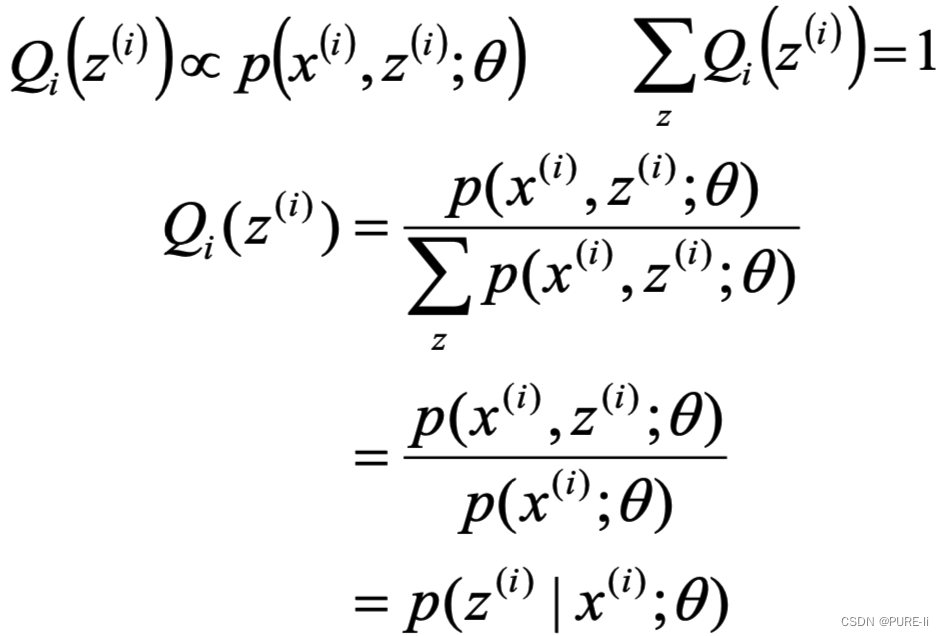
七。EM算法整体框架 

 

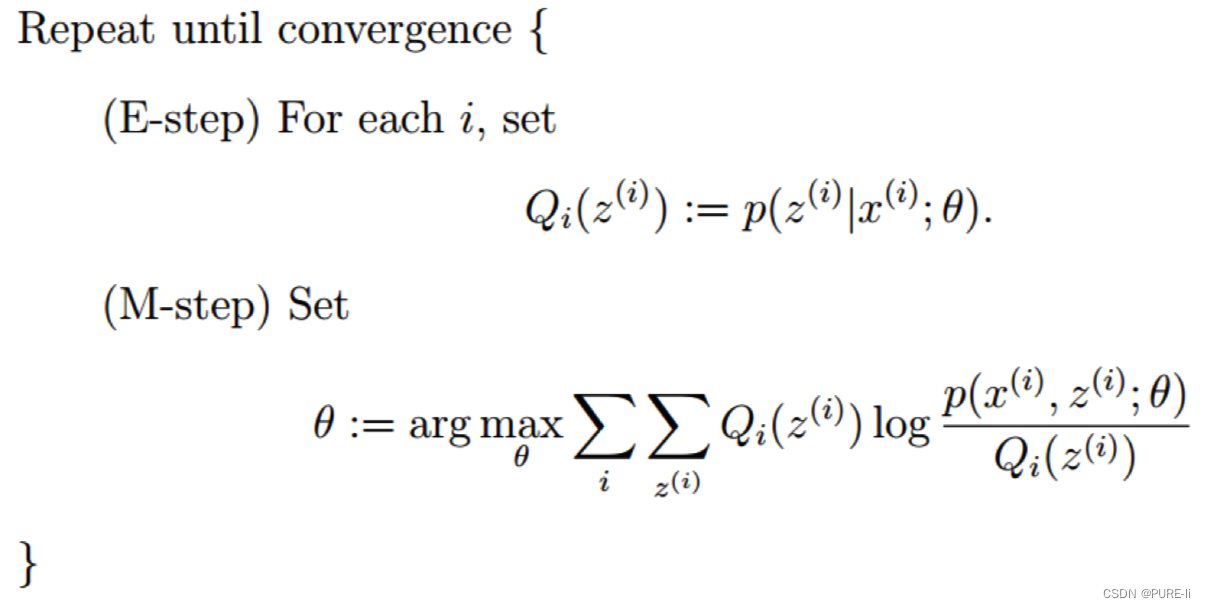
八。从理论公式推导GMM 

随机变量X是有K个高斯分布混合而成，取各个高斯分布的概率为φ1φ2... φK，第i个高斯分布的均值为μi，方差为Σi。若观测到随机变量X的一系列样本x1,x2,...,xn，试估计参数φ，μ，Σ。 

1.E-step 

2.M-step 

将多项分布和高斯分布的参数带入： 

 

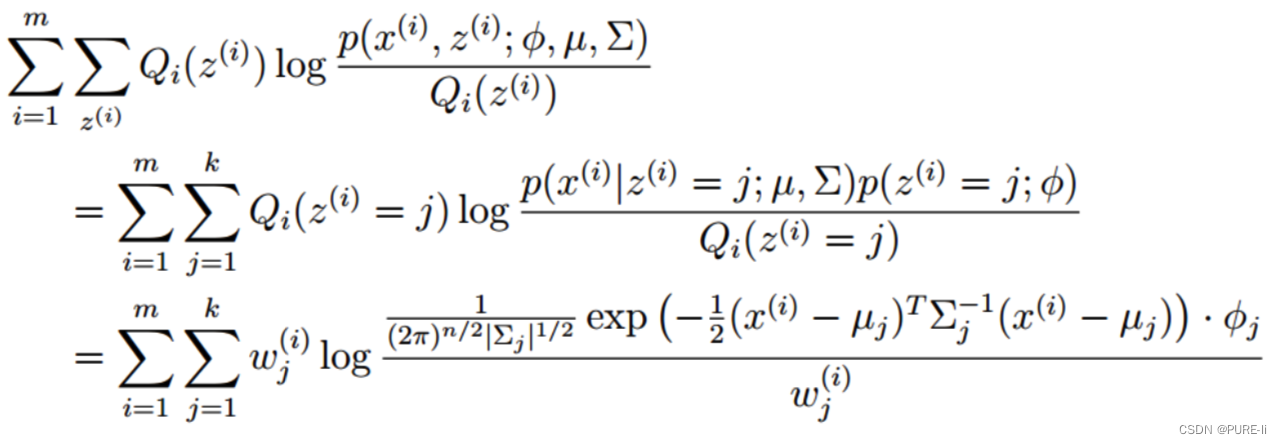
3.对均值求偏导 

 

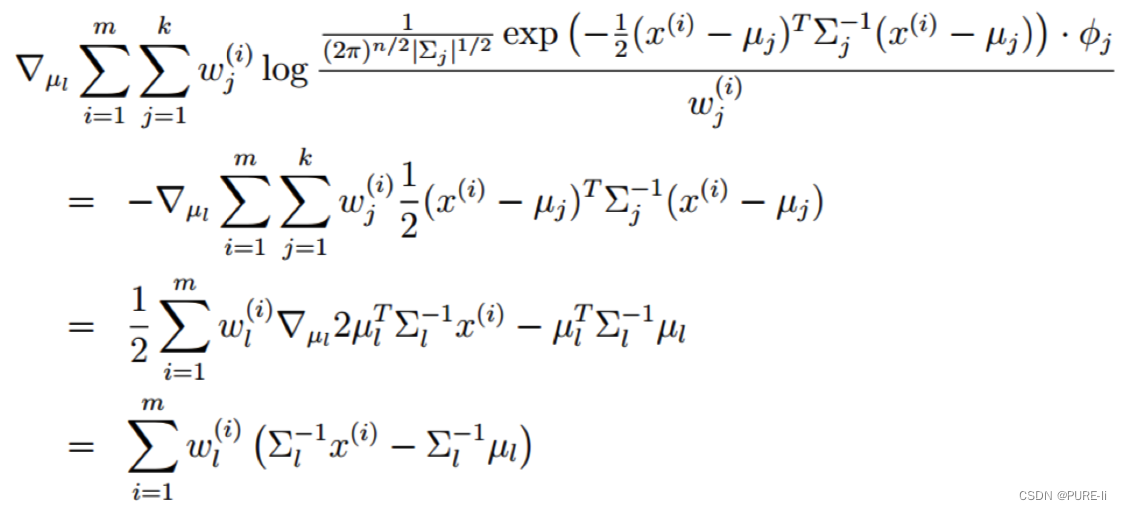
4.高斯分布的均值 

令上式等于0，解的均值： 

 

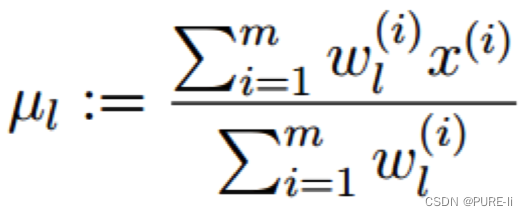
5.高斯分布的方差：求偏导，等于0 

 

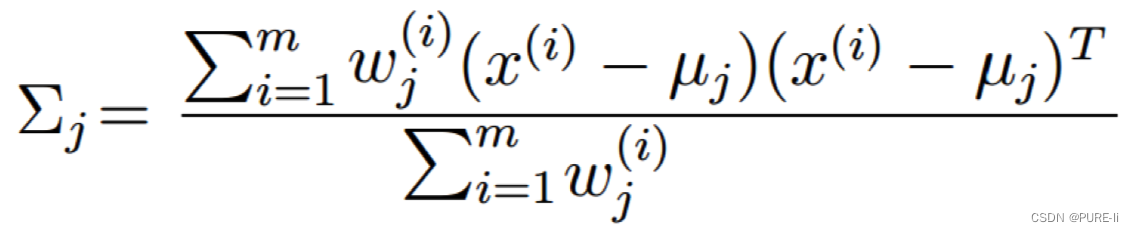
6.多项分布的参数 

考察M-step的目标函数，对于φ，删除常数项 

 

得到 

 

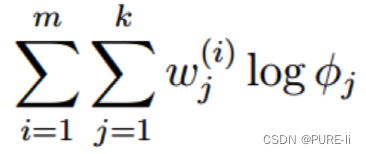
7.拉格朗日乘子法 

由于多项分布的概率和为1，建立拉格朗日方程

  

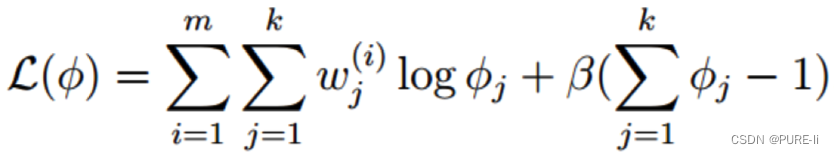
求解的φi一定非负，不用考虑φi≥0这个条件 

8.求偏导，等于0 

 

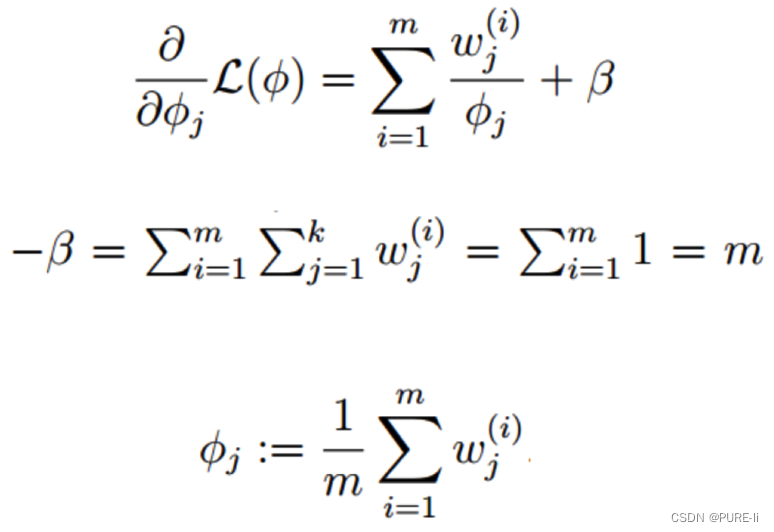
9.总结

对于所有的数据点，可以看作组份k生成了这些点。组份k是一个标准的高斯分布，利用上面的结论： 

 

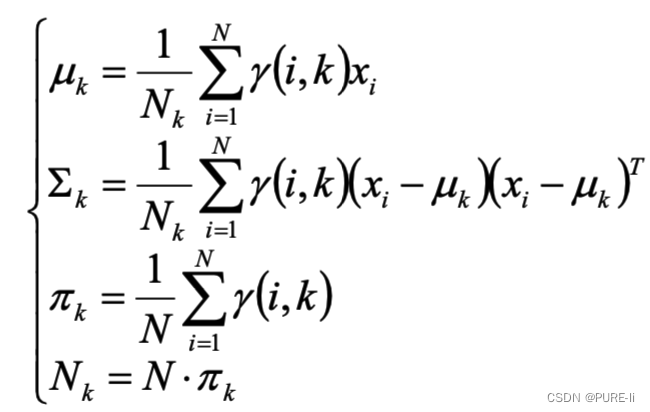
九。pLSA模型 

基于概率统计的pLSA模型(probabilistic Latent Semantic Analysis，概率隐语义分析)，增加了主题模型，形成简单的贝叶斯网络，可以使用EM算法学习模型参数。  

1.D代表文档，Z代表主题(隐含类别)，W代表单词；

        P(di)表示文档di的出现概率

        P(zk|di)表示文档di中主题zk的出现概率

        P(wj|zk)表示给定主题zk出现单词wj的概率

每个主题在所有词项上服从多项分布，每个文档在所有主题上服从多项分布。

整个文档的生成过程是这样的：

        以P(di)的概率选中文档di 

        以P(zk|k|di)的概率选中主题zk

        以P(wj|zk)的概率产生一个单词wj 

观察数据为(di,i,wj)对，主题zk是隐含变量。 

(di,wj)的联合分布为 

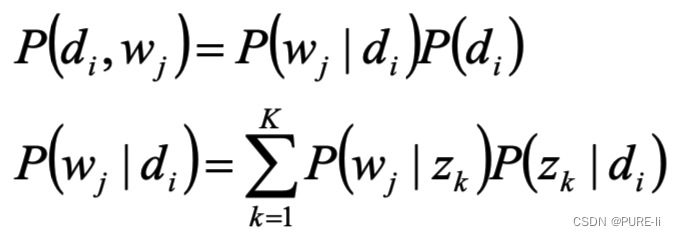
而对应了两组多项分布，而计算每个文档的主题分布，就是该模型的任务目标。  

2.最大似然估计：wj在di中出现的次数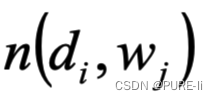 

 

3.目标函数分析  

4.求隐含变量主题zk的后验概率 

 

5.分析似然函数期望  

在(di,wj ,zk)已知的前提下，求关于参数P(zk|di)、P(wj|zk) 的似然函数期望的最大值，得到最优解P(zk|di)、P(wj|zk) ，带入上一步，从而循环迭代； 

6.关于参数P(zk|di)P(wj|zk) 的似然函数期望 

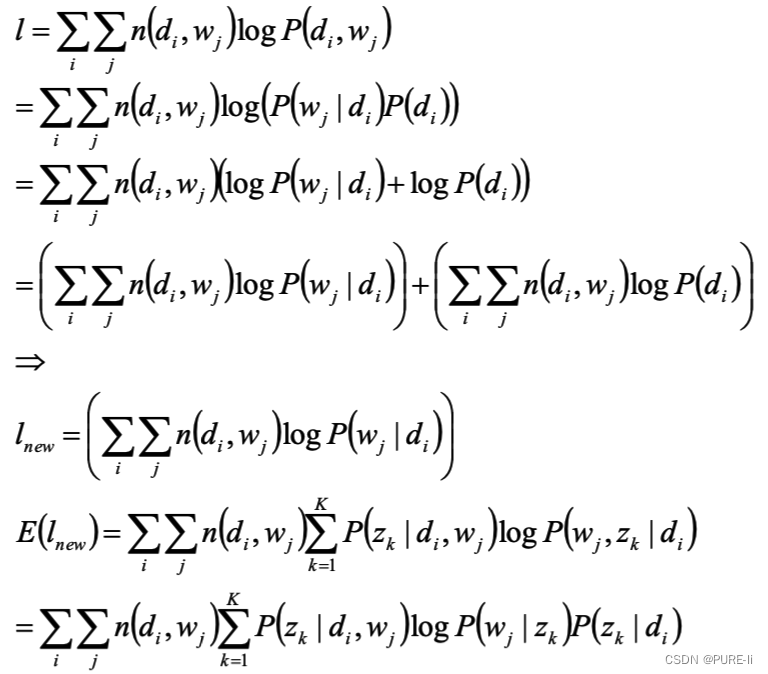
7.完成目标函数的建立 

 

显然，这是只有等式约束的求极值问题，使用Lagrange乘子法解决。  

8.目标函数的求解 

 

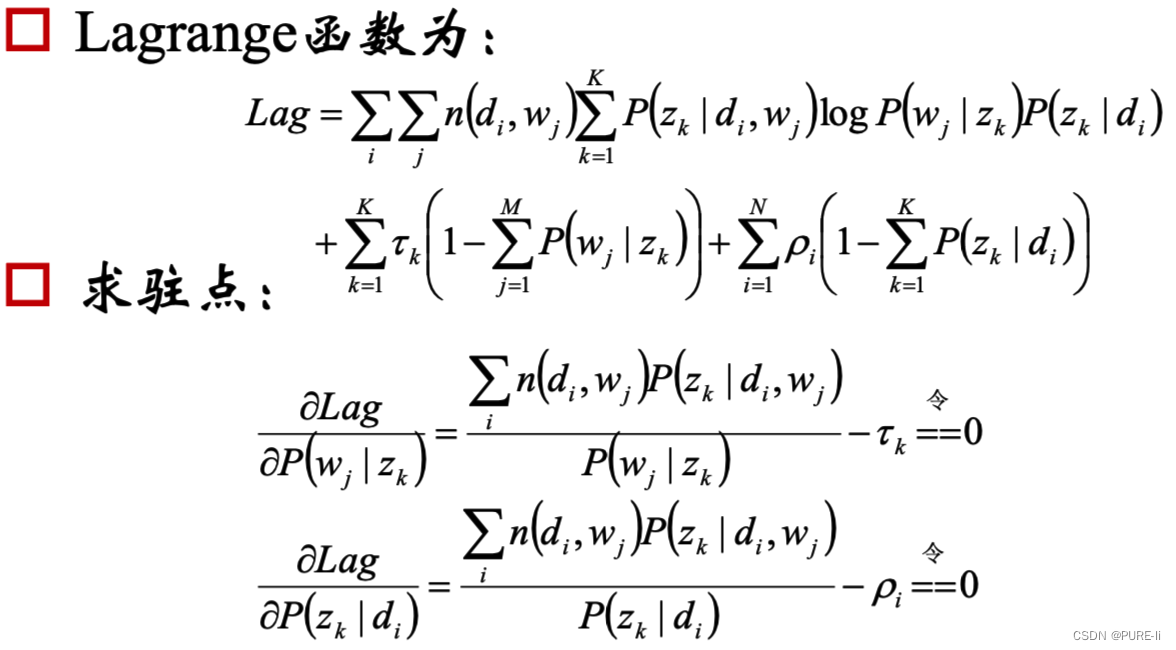
9.分析第一个等式

 

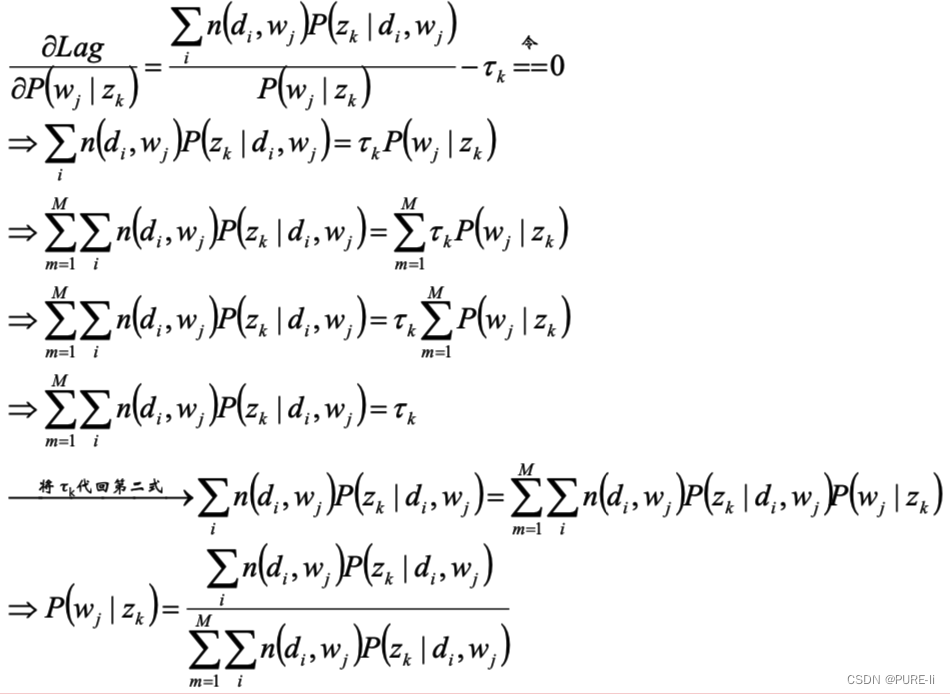
10.同理分析第二个等式 

 

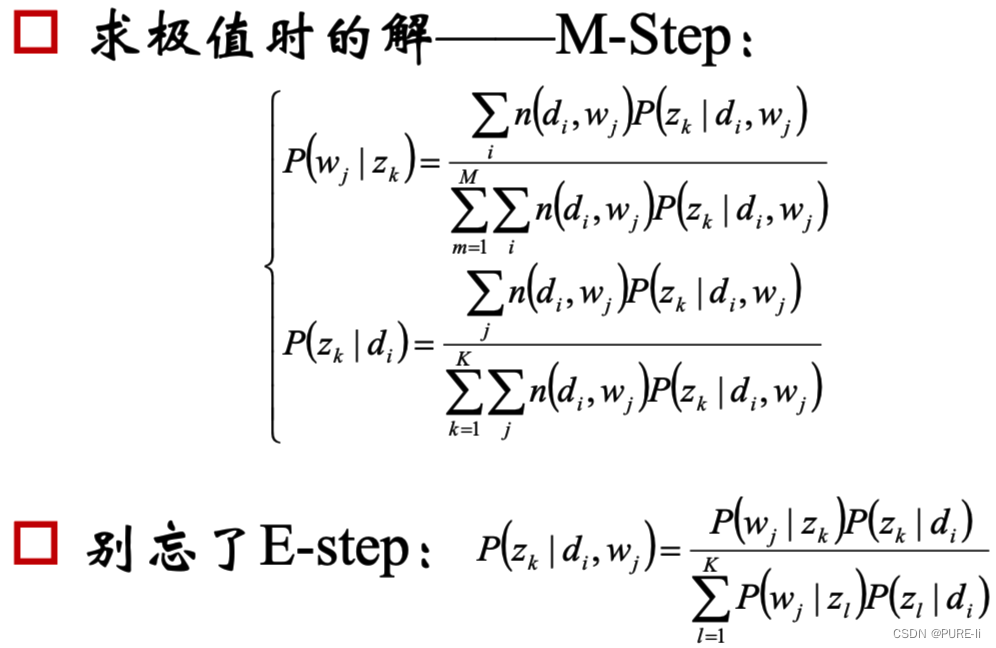
11.pLSA的总结 

pLSA应用于信息检索、过滤、自然语言处理等领域，pLSA考虑到词分布和主题分布，使用EM算法来学习参数。 
虽然推导略显复杂，但最终公式简洁清晰，很符合直观理解，需用心琢磨；此外，推导过程使用了EM算法，也是学习EM算法的重要素材。  

12. pLSA进一步思考

pLSA不需要先验信息即可完成自学习——这是它的优势。如果在特定的要求下，需要有先验知识的影响呢？ 

答：LDA模型；

        三层结构的贝叶斯模型 
        需要超参数