---

前言

1、最长递增子序列
2、最长连续递增序列
3、最长重复子数组

---

一、最长递增子序列（力扣300）

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

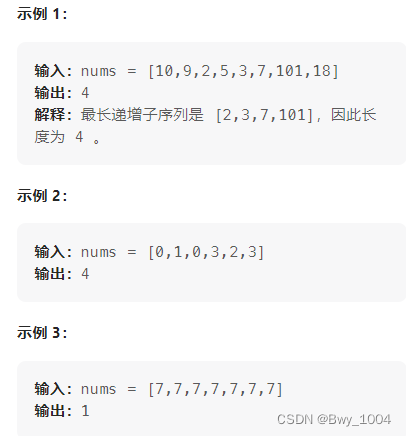
动规五部曲：
1、确定dp数组及其下标含义
dp[i]:考虑下标为i （包含i）的元素内的最长递增子序列个数为dp[i]
2、递推公式
j<i
nums[i]>nums[j] dp[i]=max(dp[j]+1, dp[i])
3、初始化
dp[0]=1
4、遍历顺序
从前往后

class Solution {
    public int lengthOfLIS(int[] nums) {
        int[] dp = new int [nums.length];
        //初始化
        for(int i=0;i<nums.length;i++){
            dp[i]=1;
        }
        //遍历顺序
        for(int i=1;i<nums.length;i++){
            for(int j=0;j<i;j++){
                if(nums[i]>nums[j])
                    dp[i] = Math.max(dp[i],dp[j]+1);
            }
        }
        int res = 0;
        for(int i=0;i<dp.length;i++){
            res = Math.max(res,dp[i]);
        }
        return res;
    }
}

为什么最后不是直接 return dp[nums.length-1]？

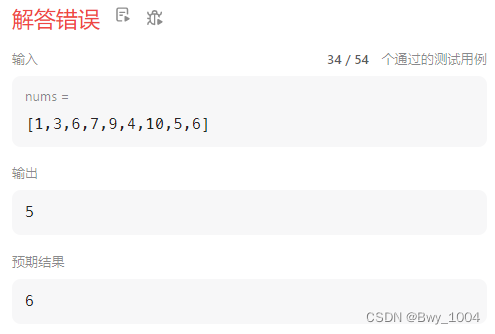
这个测试用例可以解释.

二、最长连续递增序列（力扣674）

给定一个未经排序的整数数组，找到最长且 连续递增的子序列，并返回该序列的长度。

连续递增的子序列 可以由两个下标 l 和 r（l < r）确定，如果对于每个 l <= i < r，都有 nums[i] < nums[i + 1] ，那么子序列 [nums[l], nums[l + 1], …, nums[r - 1], nums[r]] 就是连续递增子序列。

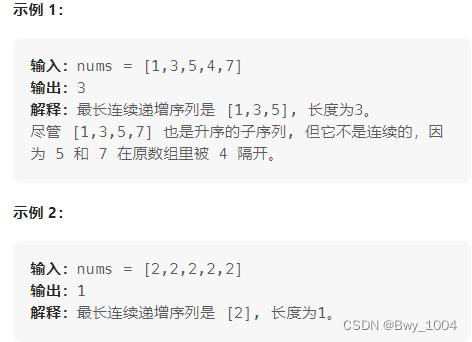
相比上一题简单一点
动规五部曲：
1、确定dp数组及其下标含义
dp[i]:考虑下标为i （包含i）的元素内的最长连续递增序列个数为dp[i]
2、递推公式
nums[i]>nums[i-1] dp[i]=dp[i-1]+1
3、初始化
dp[0]=1
4、遍历顺序
从前往后

class Solution {
    public int findLengthOfLCIS(int[] nums) {
        int[] dp =new int[nums.length];
        for(int i=0;i<nums.length;i++){
            dp[i]=1;
        }
        for(int i=1;i<nums.length;i++){
            if(nums[i]>nums[i-1]){
                dp[i] = dp[i-1]+1;
            }
        }
        int res =0;
        for(int i=0;i<dp.length;i++){
            res = Math.max(dp[i],res);
        }
        return res;
    }
}

三、最长重复子数组（力扣718）

给两个整数数组 nums1 和 nums2 ，返回 两个数组中 公共的 、长度最长的子数组的长度 。

分析：
之前使用过暴力求解

class Solution {
    public int findLength(int[] nums1, int[] nums2) {
        int k=0;
        int max=0;
        for(int j=0;j<nums2.length;j++){
            for(int i=0;i<nums1.length;){
                while(nums2[j]==nums1[i]){
                    i++;
                    j++;
                    k++;
                }
            }
        }
    }
}

时间复杂度较高，使用动态规划思想分析：
1、dp[]数组以及其下标含义【难点所在】
dp[i][j]:以i-1为结尾的nums1子数组和以j-1为结尾的nums2子数组的最长重复子数组长度。
2、递推公式
if(nums1[i-1]==nums2[j-1])
dp[i][j] = dp[i-1][j-1]+1
3、初始化
dp[i][0]=0
dp[0][j]=0
4、遍历顺序
两个数组先遍历哪个都可以
从前向后

for(int i=1;i<=nums1.length;i++){
            for(int j=1;j<=nums2.length;j++){
                if(nums1[i-1]==nums2[j-1]){
                    dp[i][j] = dp[i-1][j-1]+1;
                }
            }
        }

那么最后的结果存在哪里了？
dp[nums1.length][nums2.length]吗？
这个值求的不是我们最终想要的结果，我们需要把这个二维的dp数组全都遍历一遍，找出最长的重复子数组

如果dp数组定义中dp[i][j]: 以i结尾……以j结尾，那么我们的dp[i][j]应该初始化为什么 dp[i][0]就需要去遍历，如果相等的话，就需要将对应的位置初始化为1。同样dp[0][j]也是如此。这样就需要两个for循环

这也就是为什么在一开始的dp数组定义中dp[i][j]: 以i-1结尾……以j-1结尾，而不是直接定义为 i、j

class Solution {
    public int findLength(int[] nums1, int[] nums2) {
        int[][] dp = new int[nums1.length+1][nums2.length+1];
        int res=0;
        for(int i=1;i<=nums1.length;i++){
            for(int j=1;j<=nums2.length;j++){
                if(nums1[i-1]==nums2[j-1]){
                    dp[i][j] = dp[i-1][j-1]+1;
                }
                if(dp[i][j]>res){
                    res = dp[i][j];
                }
            }
        }
        return res;
    }
}

---