搜索技术【深度优先搜索】 - 回溯法

回溯法是一种选优搜索法，按照选优条件深度优先搜索，以达到目标。当搜索到某一步时，发现原先的选择并不是最优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术被称为回溯法，而满足回溯条件的某个状态被称为“回溯点”。

【回溯法】

算法要素

回溯法指从初始状态出发，按照深度优先搜索的方式，根据产生子节点的条件约束，搜索问题的解，当发现当前节点不满足求解条件时，就回溯，尝试其他路径。回溯法是一种“能进则进，进不了则换，换不了则退”的搜索方法。

[算法要素]

用回溯法解决实际问题时，首先要确定解的组织形式，定义问题的解空间。

① 解空间

解的组织形式： 回溯法的解的组织形式可以被规范为一个n 元组{x 1 ,x 2 ,…,xn }，例如对3个物品的0-1背包问题，解的组织形式为{x ,x 2 ,x 3 }。

显约束： 对解分量的取值范围的限定。

比如有3个物品的0-1背包问题，解的组织形式为{x 1 ,x 2 ,x 3 }。它的解分量xi 的取值范围很简单，xi =0或者xi =1。xi =0表示将第i 个物品不放入背包，xi =1表示将第i 个物品放入背包，因此xi ∈{0,1}。3个物品的0-1背包问题，其所有可能解是{0,0,0}、{0,0,1}、{0,1,0}、{0,1,1}、{1,0,0}、{1,0,1}、{1,1,0}、{1,1,1}。

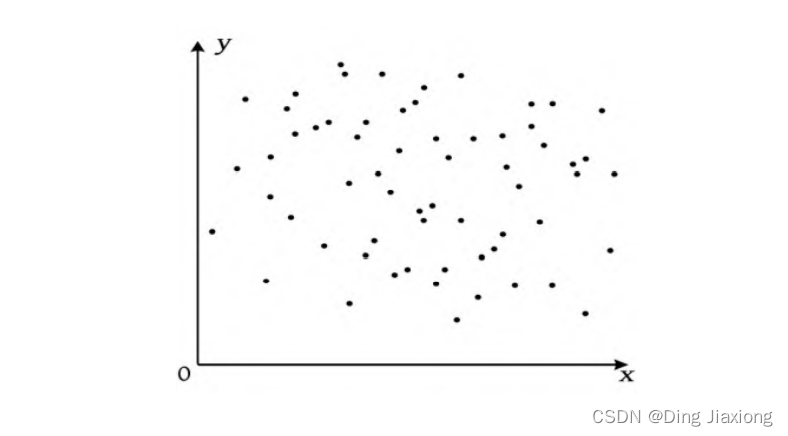
解空间： 顾名思义，就是由所有可能解组成的空间。二维解空间如下图所示。假设图中的每一个点都有可能是我们要的解，这些可能解就组成了解空间，而我们需要根据问题的约束条件，在解空间中寻找最优解。解空间越小，搜索效率越高。解空间越大，搜索效率越低。这犹如大海捞针，在大海里捞针相当困难，如果把解空间缩小到一平方米的海底就容易得多了。

② 解空间的组织结构

一个问题的解空间通常由很多可能解组成，不能像无头苍蝇一样乱飞乱撞去寻找最优解，盲目搜索的效率太低了，需要按照一定的套路即一定的组织结构搜索最优解。如果把这种组织结构用树形象地表达出来，就是解空间树。例如对3个物品的0-1背包问题，解空间树如下图所示。

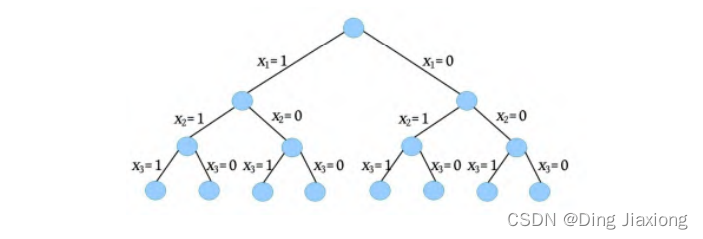
解空间树只是解空间的形象表示，有利于解题时对搜索过程有直观理解，并不是真的要生成一棵树。有了解空间树，不管是写代码还是手工搜索求解，都能看得非常清楚，更能直接看到整个搜索空间的大小。

③ 搜索解空间

隐约束：指对能否得到问题的可行解或最优解做出的约束。

如果不满足隐约束，就说明得不到问题的可行解或最优解，就没必要再沿着该节点的分支进行搜索了，相当于把这个分支剪掉了。因此隐约束也被称为剪枝函数，实质上不是剪掉该分支，而是不再搜索该分支。

例如对3个物品的0-1背包问题，如果将前两个物品放入(x 1 =1,x 2=1)后，背包超重了，就没必要再考虑是否将第3个物品放入背包的问题，如下图所示。即对圈中的分支不再搜索了，相当于剪枝了。

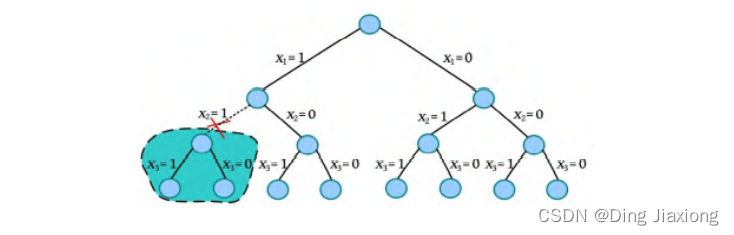
隐约束（剪枝函数）包括约束函数和限界函数。判断能否得到可行解的函数被称为约束函数，判断能否得到最优解的函数被称为限界函数。有了剪枝函数，就可以剪掉得不到可行解或最优解的分支，避免无效搜索，提高搜索效率。剪枝函数设计得好，搜索效率就高。

解空间的大小和剪枝函数的好坏都直接影响搜索效率。因此这两项是搜索算法的关键。

在搜索解空间时，有以下几个术语需要说明。

• 扩展节点：一个正在生成孩子的节点。
• 活节点：一个自身已生成，但孩子还没有全部生成的节点。
• 死节点：一个所有孩子都已经生成的节点。
• 子孙：节点e 的子树上所有节点都是e 的子孙。
• 祖宗：从节点e 到树根路径上的所有节点都是e 的祖宗。

解题秘籍

① 定义解空间。因为解空间的大小对搜索效率有很大的影响，因此使用回溯法时首先要定义合适的解空间，包括解的组织形式和显约束。

• 解的组织形式：将解的组织形式都规范为一个n 元组{x 1 ,x 2 ,…,xn }，只是对具体问题表达的含义不同而已。
• 显约束：显约束是对解分量的取值范围的限定，可以控制解空间的大小。

② 确定解空间的组织结构。解空间的组织结构通常以解空间树形象地表达，根据解空间树的不同，解空间分为子集树、排列树、m 叉树等。

③ 搜索解空间。按照深度优先搜索策略，根据隐约束（约束函数和限界函数），在解空间中搜索问题的可行解或最优解。当发现当前节点不满足求解条件时，就回溯，尝试其他路径。如果问题只是求可行解，则只需设定约束函数即可，如果要求最优解，则需要设定约束函数和限界函数。解的组织形式都是通用的n 元组形式，是解空间的形象表达。解空间和隐约束是控制搜索效率的关键。显约束可以控制解空间的大小，约束函数决定剪枝的效率，限界函数决定是否得到最优解。所以回溯法解题的关键是设计有效的显约束和隐约束。