文章目录
- 一维正态分布
- 多维正态分布
- n维正态分布
- 二维正态分布
一维正态分布
设 X ~ N ( μ , σ 2 ) X\text{\large\textasciitilde}N(\mu,\sigma^2) X~N(μ,σ2),则 X X X的概率密度为 f ( x ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}} f(x)=2πσ1e−2σ2(x−μ)2函数图像:钟形曲线, x = μ x=\mu x=μ为对称轴且为最大值点,最大值为 1 2 π σ \frac{1}{\sqrt{2\pi}\sigma} 2πσ1, σ \sigma σ越小图像越尖锐。
-
μ
=
1
,
σ
=
1
\mu=1,\sigma=1
μ=1,σ=1:

-
μ
=
0
,
σ
=
1
2
\mu=0,\sigma=\frac{1}{2}
μ=0,σ=21:
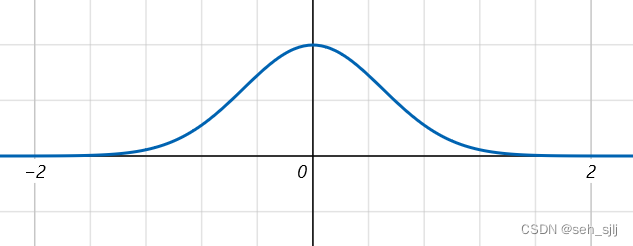
-
μ
=
0
,
σ
∈
(
0
,
5
]
\mu=0,\sigma\in(0,5]
μ=0,σ∈(0,5]:
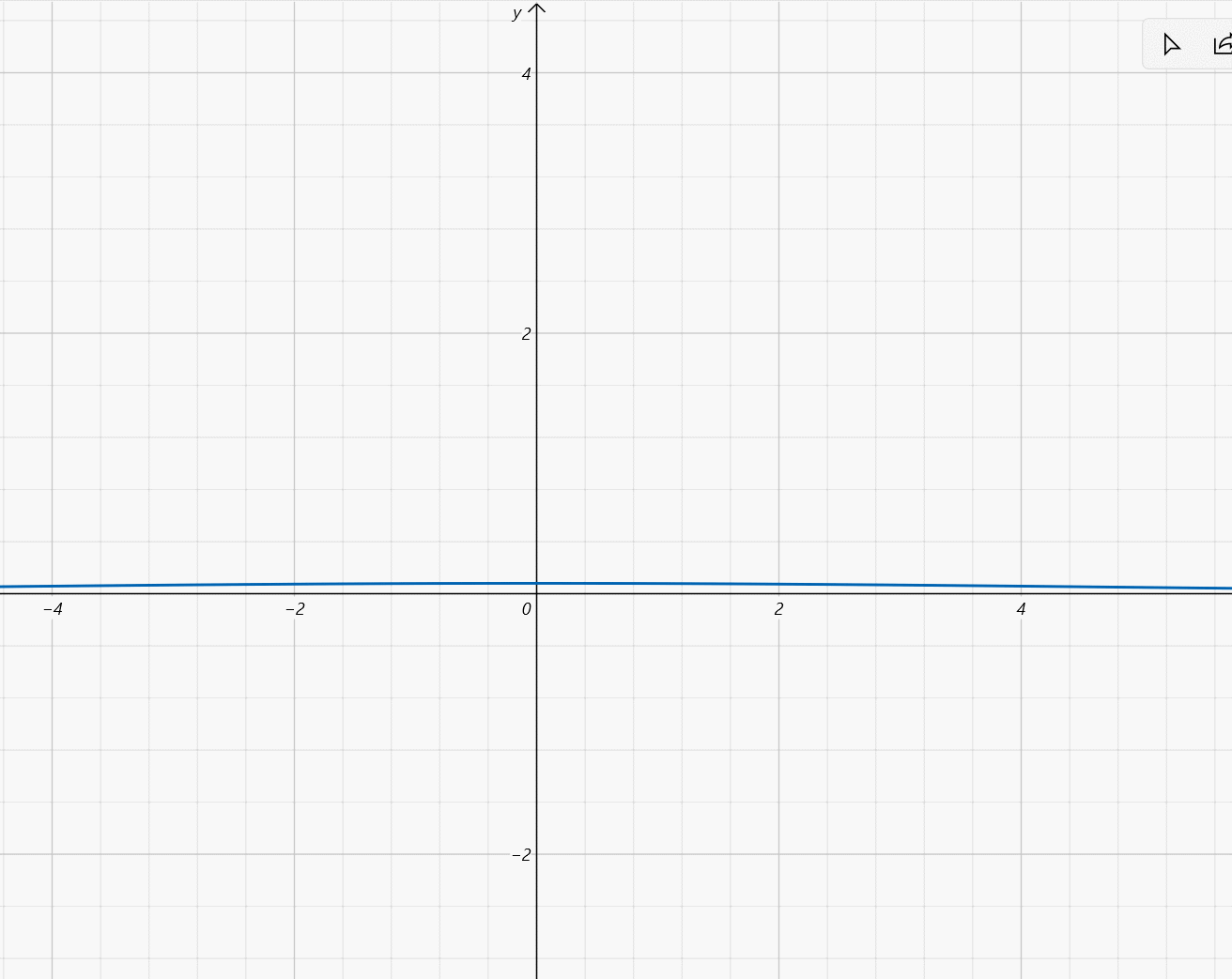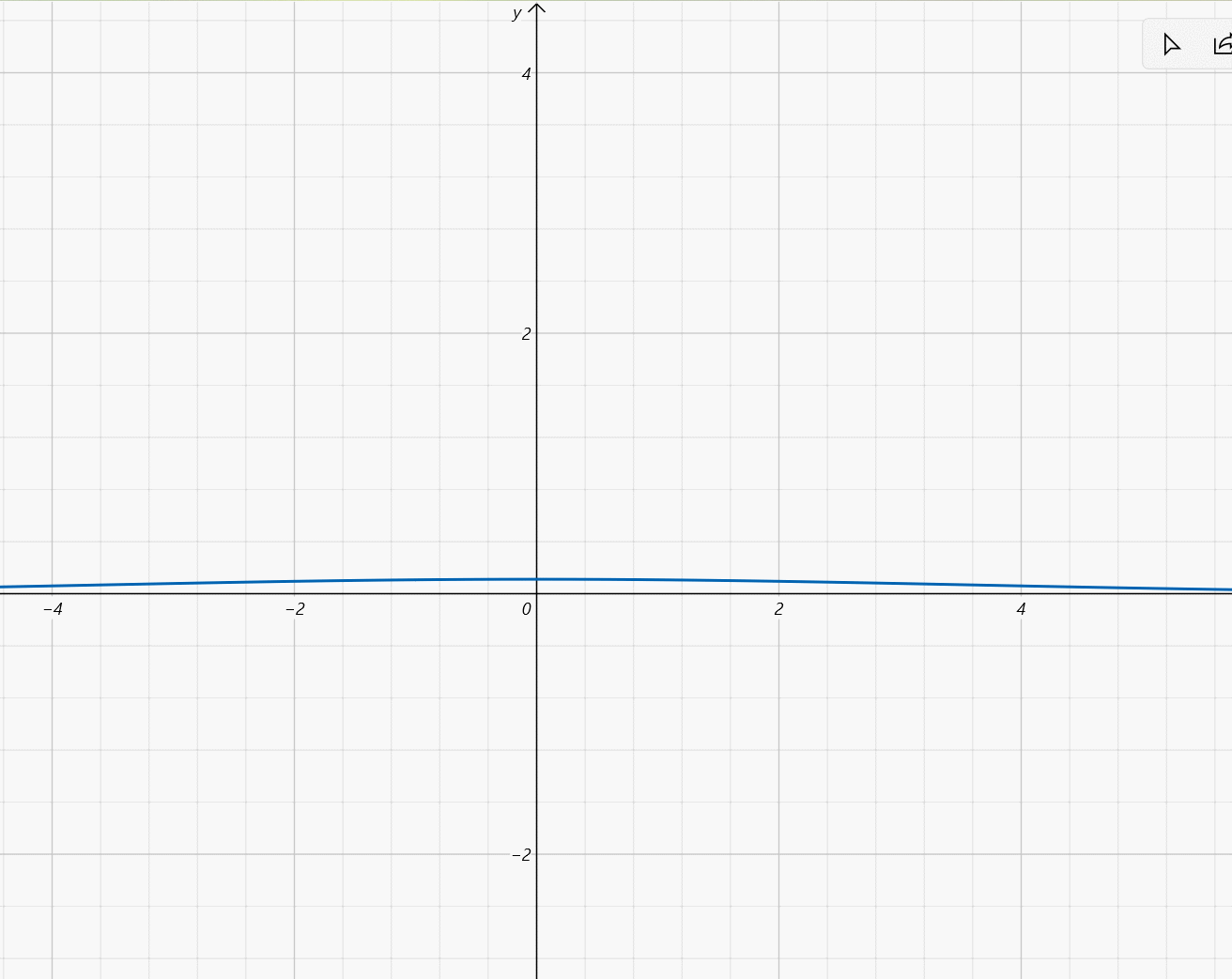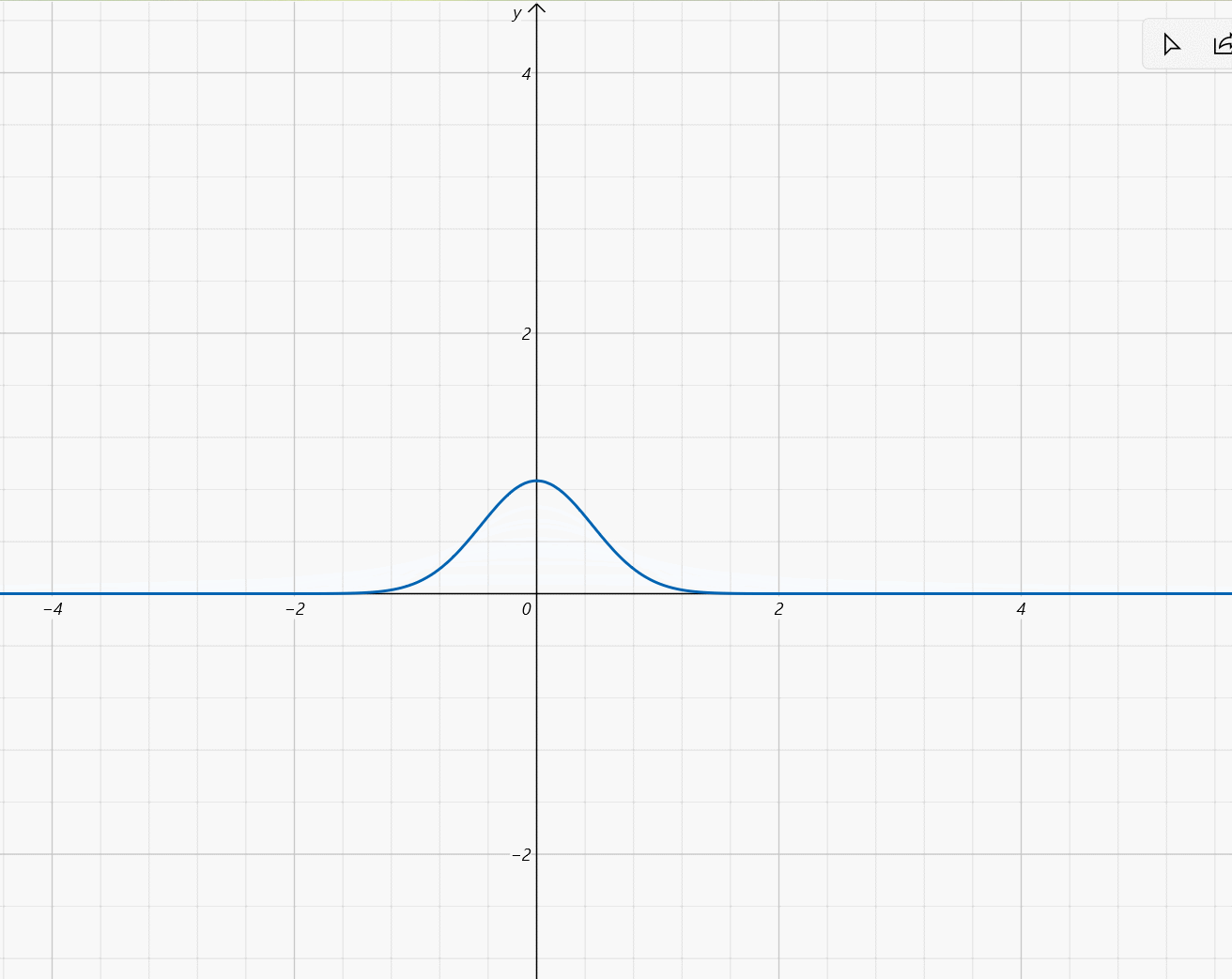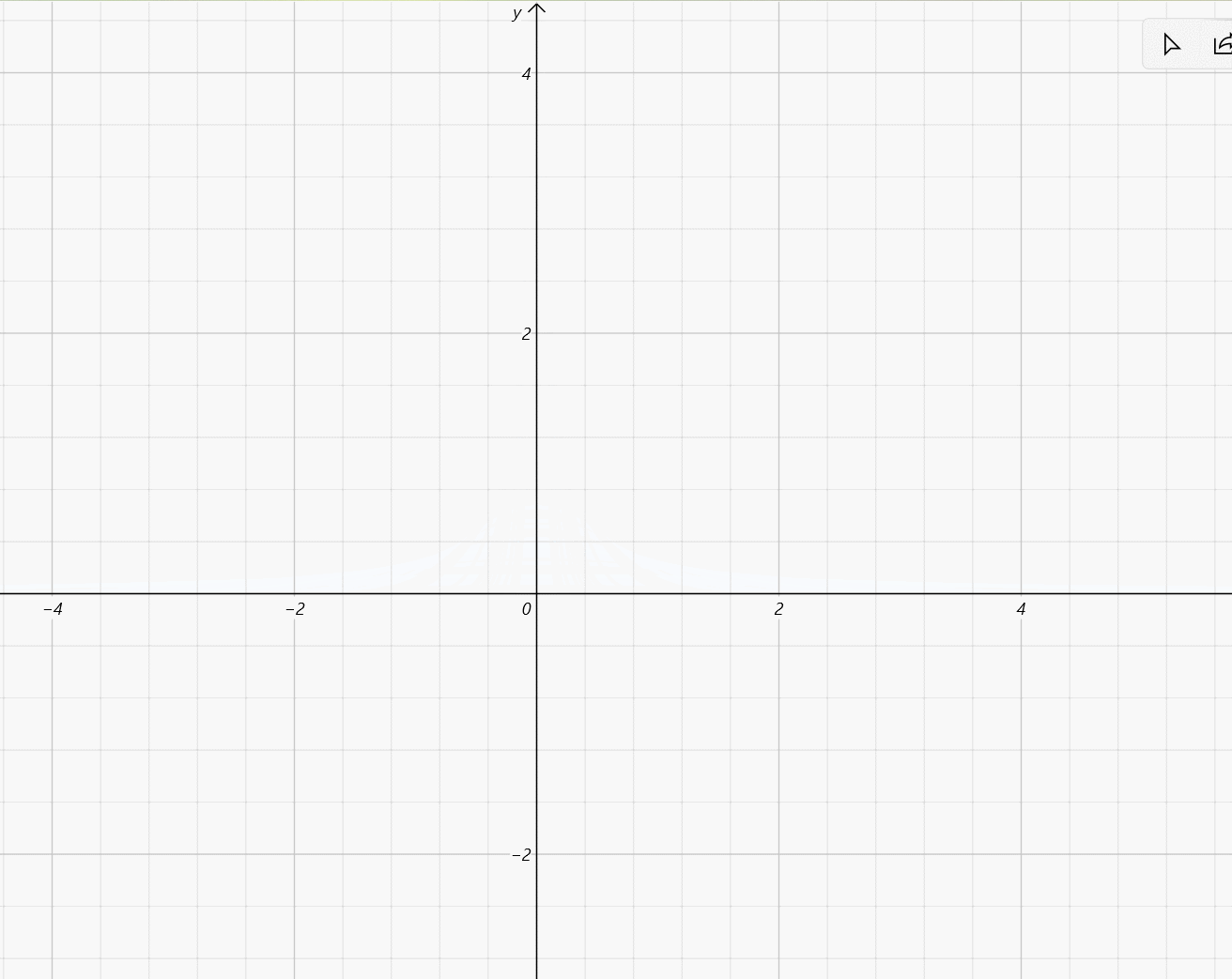
-
μ
∈
[
−
2
,
2
]
,
σ
=
1
5
\mu\in[-2,2],\sigma=\frac{1}{5}
μ∈[−2,2],σ=51:
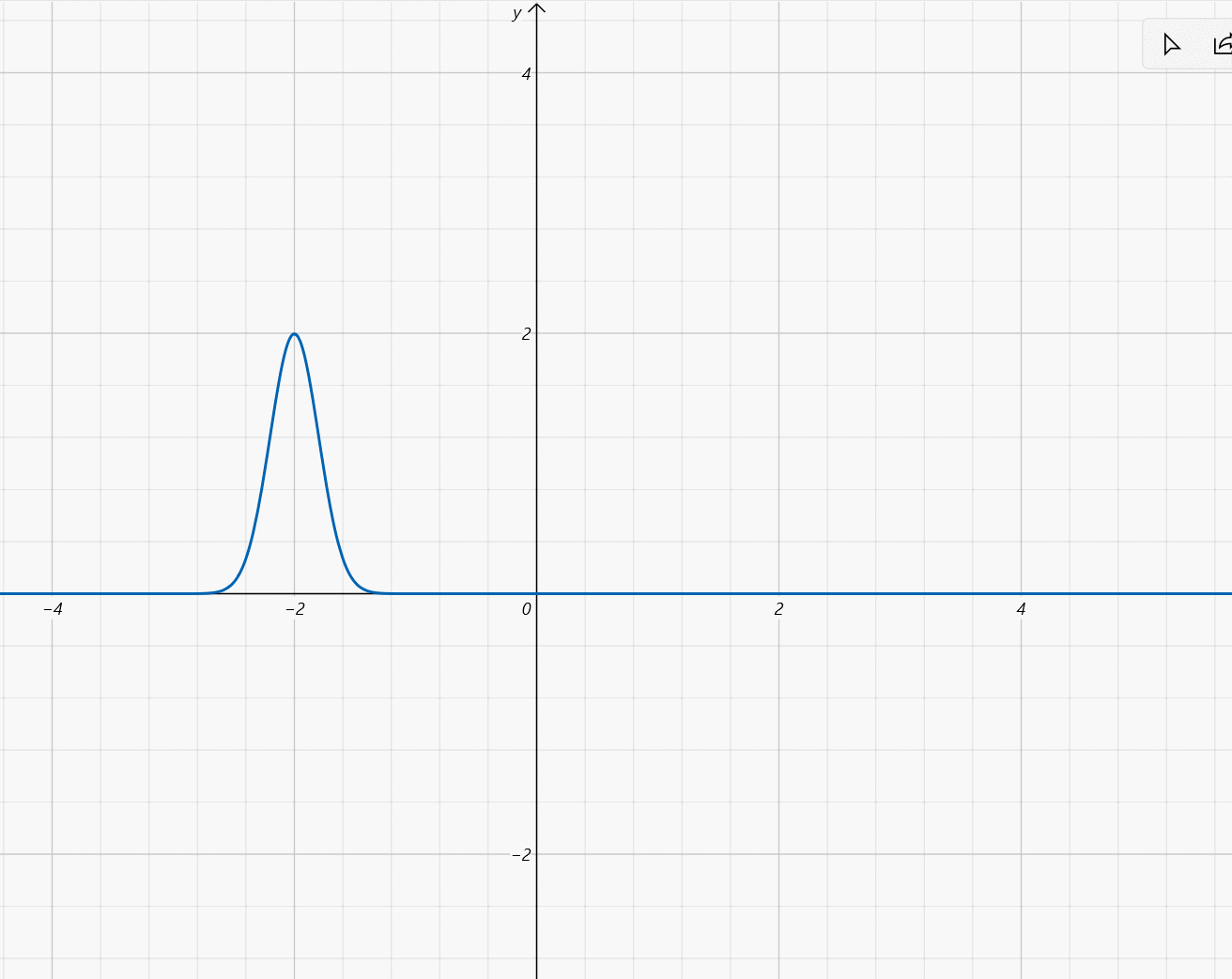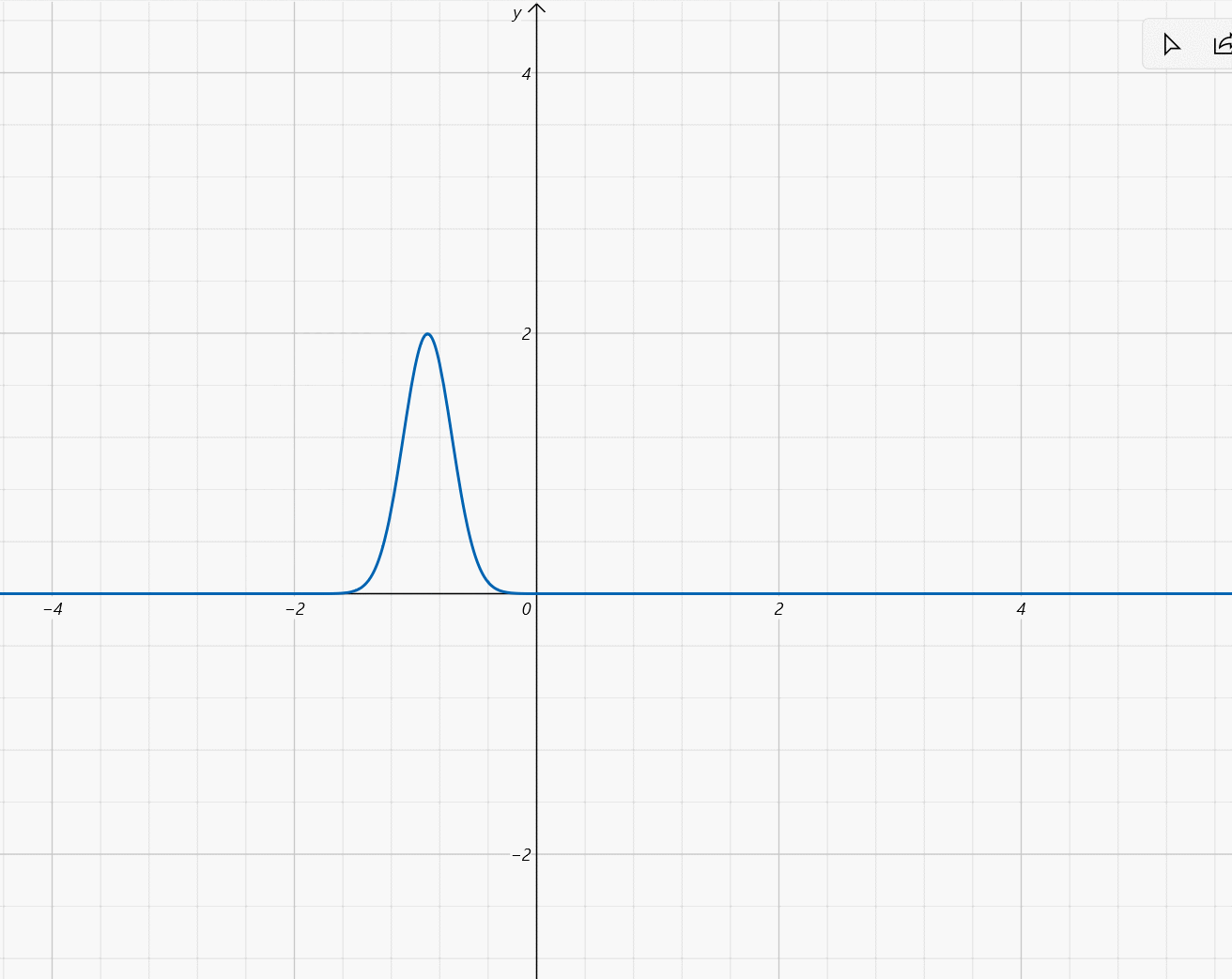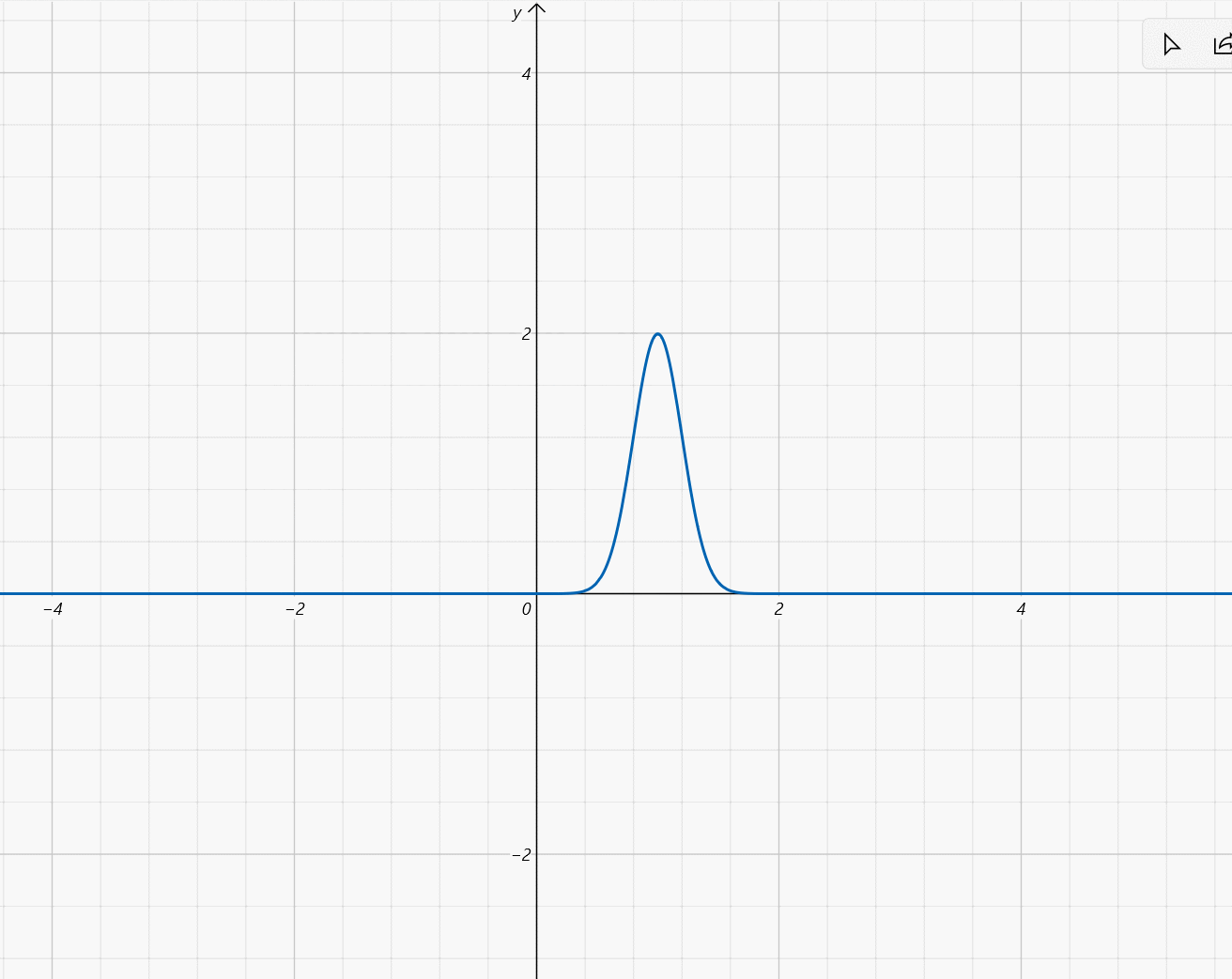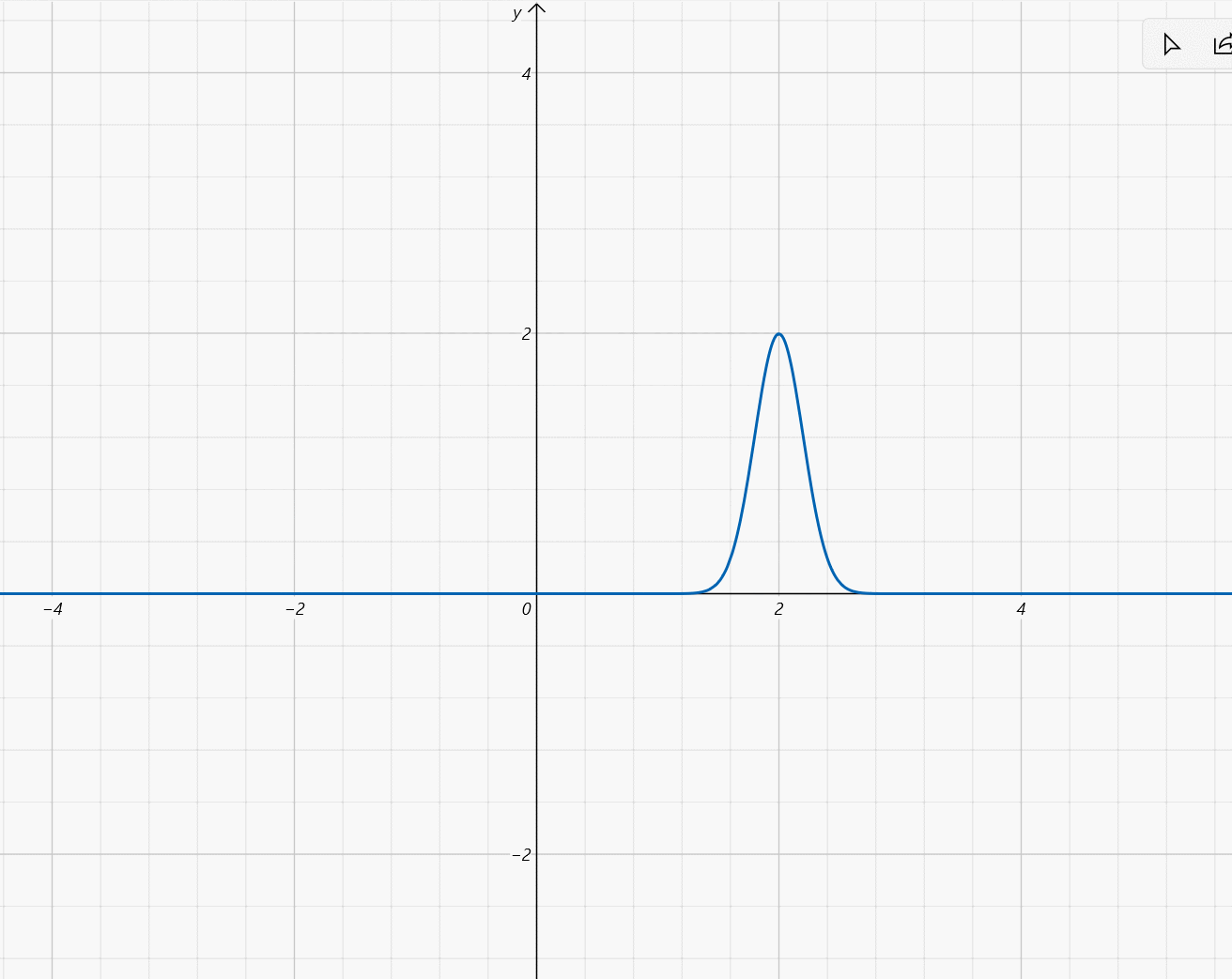
标准正态分布 N ( 0 , 1 ) N(0,1) N(0,1):设 X ~ N ( 0 , 1 ) X\text{\large\textasciitilde}N(0,1) X~N(0,1),则 X X X的概率密度函数记作 ϕ ( x ) = 1 2 π e − x 2 2 \phi(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}} ϕ(x)=2π1e−2x2 X X X的分布函数记作 Φ ( x ) \Phi(x) Φ(x),满足 Φ ( 0 ) = 1 2 , Φ ( − x ) = 1 − Φ ( x ) \Phi(0)=\frac{1}{2},\quad\Phi(-x)=1-\Phi(x) Φ(0)=21,Φ(−x)=1−Φ(x)若 X ~ N ( μ , σ 2 ) X\text{\large\textasciitilde}N(\mu,\sigma^2) X~N(μ,σ2),则 Z = X − μ σ ~ N ( 0 , 1 ) Z=\frac{X-\mu}{\sigma}\text{\large\textasciitilde}N(0,1) Z=σX−μ~N(0,1)。
X ~ N ( μ , σ 2 ) ⟹ Y = k X + b ~ N ( k μ + b , k 2 σ 2 ) X\text{\large\textasciitilde}N(\mu,\sigma^2)\implies Y=kX+b\,\text{\large\textasciitilde}\,N(k\mu+b,k^2\sigma^2) X~N(μ,σ2)⟹Y=kX+b~N(kμ+b,k2σ2)(其中 b ≠ 0 b\ne0 b=0)
X ~ N ( μ , σ 2 ) ⟹ E ( X ) = μ , D ( X ) = σ 2 , σ ( x ) = σ X\text{\large\textasciitilde}N(\mu,\sigma^2)\implies E(X)=\mu,\ D(X)=\sigma^2,\ \sigma(x)=\sigma X~N(μ,σ2)⟹E(X)=μ, D(X)=σ2, σ(x)=σ
中心极限定理:
| 中心极限定理 | 条件 | 结论(当 n n n足够大时近似成立) |
|---|---|---|
| 独立同分布中心极限定理 | 有有限的数学期望 E ( X k ) = μ E(X_k)=\mu E(Xk)=μ和方差 D ( X k ) = σ 2 ≠ 0 D(X_k)=\sigma^2\ne0 D(Xk)=σ2=0 | X ‾ ~ N ( μ , σ 2 n ) , ∑ k = 1 n X k ~ N ( n μ , n σ 2 ) \overline{X}\text{\large\textasciitilde}N\left(\mu,\frac{\sigma^2}{n}\right),\ \sum\limits_{k=1}^n X_k\text{\large\textasciitilde}N\left(n\mu,n\sigma^2\right) X~N(μ,nσ2), k=1∑nXk~N(nμ,nσ2) |
| 棣莫弗-拉普拉斯中心极限定理 | η n ~ B ( n , p ) \eta_n\text{\large\textasciitilde}B(n,p) ηn~B(n,p) | X ‾ ~ N ( p , p ( 1 − p ) n ) , η n ~ N ( n p , n p ( 1 − p ) ) \overline{X}\text{\large\textasciitilde}N\left(p,\frac{p(1-p)}{n}\right),\ \eta_n\text{\large\textasciitilde}N(np,np(1-p)) X~N(p,np(1−p)), ηn~N(np,np(1−p)) |
多维正态分布
n维正态分布
设 V \bm{V} V为 n n n阶正定对称阵, μ = ( μ 1 , μ 2 , ⋯ , μ n ) \bm{\mu}=(\mu_1,\mu_2,\cdots,\mu_n) μ=(μ1,μ2,⋯,μn)为 n n n维已知向量。记 x = ( x 1 , x 2 , ⋯ , x n ) ∈ R n \bm{x}=(x_1,x_2,\cdots,x_n)\in\mathbb R^n x=(x1,x2,⋯,xn)∈Rn。若 n n n维随机向量 X = ( X 1 , X 2 , ⋯ , X n ) \bm{X}=(X_1,X_2,\cdots,X_n) X=(X1,X2,⋯,Xn)的概率密度为 f ( x ) = 1 ( 2 π ) n 2 ∣ V ∣ 1 2 exp { − 1 2 ( x − μ ) V − 1 ( x − μ ) T } f(\bm{x})=\frac{1}{(2\pi)^{\frac{n}{2}}|\bm{V}|^{\frac{1}{2}}}\exp\left\{-\frac{1}{2}(\bm{x}-\bm{\mu})\bm{V}^{-1}(\bm{x}-\bm{\mu})^T\right\} f(x)=(2π)2n∣V∣211exp{−21(x−μ)V−1(x−μ)T}则称 X \bm{X} X服从 n n n维正态分布,记作 X = ( X 1 , X 2 , ⋯ , X n ) ~ N ( μ , V ) \bm{X}=(X_1,X_2,\cdots,X_n)\text{\large\textasciitilde}N(\bm{\mu},\bm{V}) X=(X1,X2,⋯,Xn)~N(μ,V)。
n
n
n维正态分布的基本性质:
设
X
=
(
X
1
,
X
2
,
⋯
,
X
n
)
~
N
(
μ
,
V
)
\bm{X}=(X_1,X_2,\cdots,X_n)\text{\large\textasciitilde}N(\bm{\mu},\bm{V})
X=(X1,X2,⋯,Xn)~N(μ,V),则:
(1)
μ
i
=
E
(
X
i
)
(
i
=
1
,
2
,
⋯
,
n
)
\mu_i=E(X_i)(i=1,2,\cdots,n)
μi=E(Xi)(i=1,2,⋯,n);
(2)
V
=
(
v
i
j
)
n
×
n
\bm{V}=(v_{ij})_{n\times n}
V=(vij)n×n是
X
\bm{X}
X的协方差矩阵,且
D
(
X
i
)
=
v
i
i
D(X_i)=v_{ii}
D(Xi)=vii,
Cov
(
X
i
,
X
j
)
=
v
i
j
(
i
,
j
=
1
,
2
,
⋯
,
n
)
\text{Cov}(X_i,X_j)=v_{ij}(i,j=1,2,\cdots,n)
Cov(Xi,Xj)=vij(i,j=1,2,⋯,n);
(3)
X
i
~
N
(
μ
i
,
v
i
i
)
X_i\text{\large\textasciitilde}N(\mu_i,v_{ii})
Xi~N(μi,vii);
(4)
X
1
,
X
2
,
⋯
,
X
n
X_1,X_2,\cdots,X_n
X1,X2,⋯,Xn相互独立
⟺
X
1
,
X
2
,
⋯
,
X
n
{\color{red}\iff}X_1,X_2,\cdots,X_n
⟺X1,X2,⋯,Xn两两互不相关
⟺
V
=
diag
(
v
11
,
v
22
,
⋯
,
v
n
n
)
\iff\bm{V}=\text{diag}(v_{11},v_{22},\cdots,v_{nn})
⟺V=diag(v11,v22,⋯,vnn);
(5) 若
X
1
,
X
2
,
⋯
,
X
n
X_1,X_2,\cdots,X_n
X1,X2,⋯,Xn相互独立,且各
X
i
~
N
(
μ
i
,
σ
i
2
)
X_i\text{\large\textasciitilde}N(\mu_i,\sigma_i^2)
Xi~N(μi,σi2),则
(
X
1
,
X
2
,
⋯
,
X
n
)
~
N
(
μ
,
V
)
(X_1,X_2,\cdots,X_n)\text{\large\textasciitilde}N(\bm{\mu},\bm{V})
(X1,X2,⋯,Xn)~N(μ,V),其中
μ
=
(
μ
1
,
μ
2
,
⋯
,
μ
n
)
\bm{\mu}=(\mu_1,\mu_2,\cdots,\mu_n)
μ=(μ1,μ2,⋯,μn),
V
=
diag
(
σ
1
2
,
σ
2
2
,
⋯
,
σ
n
2
)
\bm{V}=\text{diag}(\sigma_1^2,\sigma_2^2,\cdots,\sigma_n^2)
V=diag(σ12,σ22,⋯,σn2);
(6)
(
X
1
,
X
2
,
⋯
,
X
n
)
~
N
(
μ
,
V
)
⟺
X
1
,
X
2
,
⋯
,
X
n
(X_1,X_2,\cdots,X_n)\text{\large\textasciitilde}N(\bm{\mu},\bm{V})\iff X_1,X_2,\cdots,X_n
(X1,X2,⋯,Xn)~N(μ,V)⟺X1,X2,⋯,Xn的任一非零线性组合
l
1
X
1
+
l
2
X
2
+
⋯
+
l
n
X
n
l_1X_1+l_2X_2+\cdots+l_nX_n
l1X1+l2X2+⋯+lnXn服从一维正态分布;
(7)(正态随机向量的线性变换不变性) 若
(
X
1
,
X
2
,
⋯
,
X
n
)
~
N
(
μ
,
V
)
(X_1,X_2,\cdots,X_n)\text{\large\textasciitilde}N(\bm{\mu},\bm{V})
(X1,X2,⋯,Xn)~N(μ,V),令
{
Y
1
=
a
11
X
1
+
a
12
X
2
+
⋯
+
a
1
n
X
n
Y
2
=
a
21
X
1
+
a
22
X
2
+
⋯
+
a
2
n
X
n
⋮
Y
m
=
a
m
1
X
1
+
a
m
2
X
2
+
⋯
+
a
m
n
X
n
\begin{cases}Y_1=a_{11}X_1+a_{12}X_2+\cdots+a_{1n}X_n\\Y_2=a_{21}X_1+a_{22}X_2+\cdots+a_{2n}X_n\\\vdots\\Y_m=a_{m1}X_1+a_{m2}X_2+\cdots+a_{mn}X_n\end{cases}
⎩
⎨
⎧Y1=a11X1+a12X2+⋯+a1nXnY2=a21X1+a22X2+⋯+a2nXn⋮Ym=am1X1+am2X2+⋯+amnXn则
Y
=
(
Y
1
,
Y
2
,
⋯
,
Y
m
)
\bm{Y}=(Y_1,Y_2,\cdots,Y_m)
Y=(Y1,Y2,⋯,Ym)仍服从多维正态分布。
二维正态分布
( X , Y ) ~ N ( μ 1 , μ 2 ; σ 1 2 , σ 2 2 ; ρ ) (X,Y)\text{\large\textasciitilde}N(\mu_1,\mu_2;\sigma_1^2,\sigma_2^2;\rho) (X,Y)~N(μ1,μ2;σ12,σ22;ρ),则其概率密度为 f ( x , y ) = 1 2 π σ 1 σ 2 1 − ρ 2 e − 1 2 ( 1 − ρ 2 ) [ ( x − μ 1 ) 2 σ 1 2 − 2 ρ ( x − μ 1 ) ( y − μ 2 ) σ 1 σ 2 + ( y − μ 2 ) 2 σ 2 2 ] , x , y ∈ R f(x,y)=\frac{1}{2\pi\sigma_1\sigma_2\sqrt{1-\rho^2}}e^{-\frac{1}{2(1-\rho^2)}\left[\frac{(x-\mu_1)^2}{\sigma_1^2}-2\rho\frac{(x-\mu_1)(y-\mu_2)}{\sigma_1\sigma_2}+\frac{(y-\mu_2)^2}{\sigma_2^2}\right]},x,y\in\mathbb R f(x,y)=2πσ1σ21−ρ21e−2(1−ρ2)1[σ12(x−μ1)2−2ρσ1σ2(x−μ1)(y−μ2)+σ22(y−μ2)2],x,y∈R其中 ρ \rho ρ就是 X X X和 Y Y Y的相关系数, X ~ N ( μ 1 , σ 1 2 ) X\text{\large\textasciitilde}N(\mu_1,\sigma_1^2) X~N(μ1,σ12), Y ~ N ( μ 2 , σ 2 2 ) Y\text{\large\textasciitilde}N(\mu_2,\sigma_2^2) Y~N(μ2,σ22)。
推导过程:
Cov
(
X
,
Y
)
=
ρ
(
X
,
Y
)
D
(
x
)
D
(
Y
)
=
ρ
σ
1
σ
2
\text{Cov}(X,Y)=\rho(X,Y)\sqrt{D(x)}\sqrt{D(Y)}=\rho\sigma_1\sigma_2
Cov(X,Y)=ρ(X,Y)D(x)D(Y)=ρσ1σ2
V
=
(
D
(
x
)
Cov
(
X
,
Y
)
Cov
(
X
,
Y
)
D
(
Y
)
)
=
(
σ
1
2
ρ
σ
1
σ
2
ρ
σ
1
σ
2
σ
2
2
)
\bm{V}=\begin{pmatrix}D(x)&\text{Cov}(X,Y)\\\text{Cov}(X,Y)&D(Y)\end{pmatrix}=\begin{pmatrix}\sigma_1^2&\rho\sigma_1\sigma_2\\\rho\sigma_1\sigma_2&\sigma_2^2\end{pmatrix}
V=(D(x)Cov(X,Y)Cov(X,Y)D(Y))=(σ12ρσ1σ2ρσ1σ2σ22)
det
(
V
)
=
σ
1
2
σ
2
2
−
ρ
2
σ
1
2
σ
2
2
=
(
1
−
ρ
2
)
σ
1
2
σ
2
2
\det(\bm{V})=\sigma_1^2\sigma_2^2-\rho^2\sigma_1^2\sigma_2^2=(1-\rho^2)\sigma_1^2\sigma_2^2
det(V)=σ12σ22−ρ2σ12σ22=(1−ρ2)σ12σ22
V
−
1
=
1
∣
V
∣
(
σ
2
2
−
ρ
σ
1
σ
2
−
ρ
σ
1
σ
2
σ
1
2
)
\bm{V}^{-1}=\frac{1}{|\bm{V}|}\begin{pmatrix}\sigma_2^2&-\rho\sigma_1\sigma_2\\-\rho\sigma_1\sigma_2&\sigma_1^2\end{pmatrix}
V−1=∣V∣1(σ22−ρσ1σ2−ρσ1σ2σ12)
(
x
−
μ
)
V
−
1
(
x
−
μ
)
T
=
1
(
1
−
ρ
2
)
σ
1
2
σ
2
2
[
σ
2
2
(
x
−
μ
1
)
2
−
2
ρ
σ
1
σ
2
(
x
−
μ
1
)
(
y
−
μ
2
)
+
σ
1
2
(
x
−
μ
2
)
2
]
(\bm{x}-\bm{\mu})\bm{V}^{-1}(\bm{x}-\bm{\mu})^T=\frac{1}{(1-\rho^2)\sigma_1^2\sigma_2^2}\left[\sigma_2^2(x-\mu_1)^2-2\rho\sigma_1\sigma_2(x-\mu_1)(y-\mu_2)+\sigma_1^2(x-\mu_2)^2\right]
(x−μ)V−1(x−μ)T=(1−ρ2)σ12σ221[σ22(x−μ1)2−2ρσ1σ2(x−μ1)(y−μ2)+σ12(x−μ2)2]化简得
(
x
−
μ
)
V
−
1
(
x
−
μ
)
T
=
1
(
1
−
ρ
2
)
[
(
x
−
μ
1
)
2
σ
1
2
−
2
ρ
(
x
−
μ
1
)
(
y
−
μ
2
)
σ
1
σ
2
+
(
y
−
μ
2
)
2
σ
2
2
]
(\bm{x}-\bm{\mu})\bm{V}^{-1}(\bm{x}-\bm{\mu})^T=\frac{1}{(1-\rho^2)}\left[\frac{(x-\mu_1)^2}{\sigma_1^2}-2\rho\frac{(x-\mu_1)(y-\mu_2)}{\sigma_1\sigma_2}+\frac{(y-\mu_2)^2}{\sigma_2^2}\right]
(x−μ)V−1(x−μ)T=(1−ρ2)1[σ12(x−μ1)2−2ρσ1σ2(x−μ1)(y−μ2)+σ22(y−μ2)2]将以上式子代入多维正态分布的概率密度函数公式,即得
f
(
x
,
y
)
=
1
2
π
σ
1
σ
2
1
−
ρ
2
e
−
1
2
(
1
−
ρ
2
)
[
(
x
−
μ
1
)
2
σ
1
2
−
2
ρ
(
x
−
μ
1
)
(
y
−
μ
2
)
σ
1
σ
2
+
(
y
−
μ
2
)
2
σ
2
2
]
,
x
,
y
∈
R
f(x,y)=\frac{1}{2\pi\sigma_1\sigma_2\sqrt{1-\rho^2}}e^{-\frac{1}{2(1-\rho^2)}\left[\frac{(x-\mu_1)^2}{\sigma_1^2}-2\rho\frac{(x-\mu_1)(y-\mu_2)}{\sigma_1\sigma_2}+\frac{(y-\mu_2)^2}{\sigma_2^2}\right]},x,y\in\mathbb R
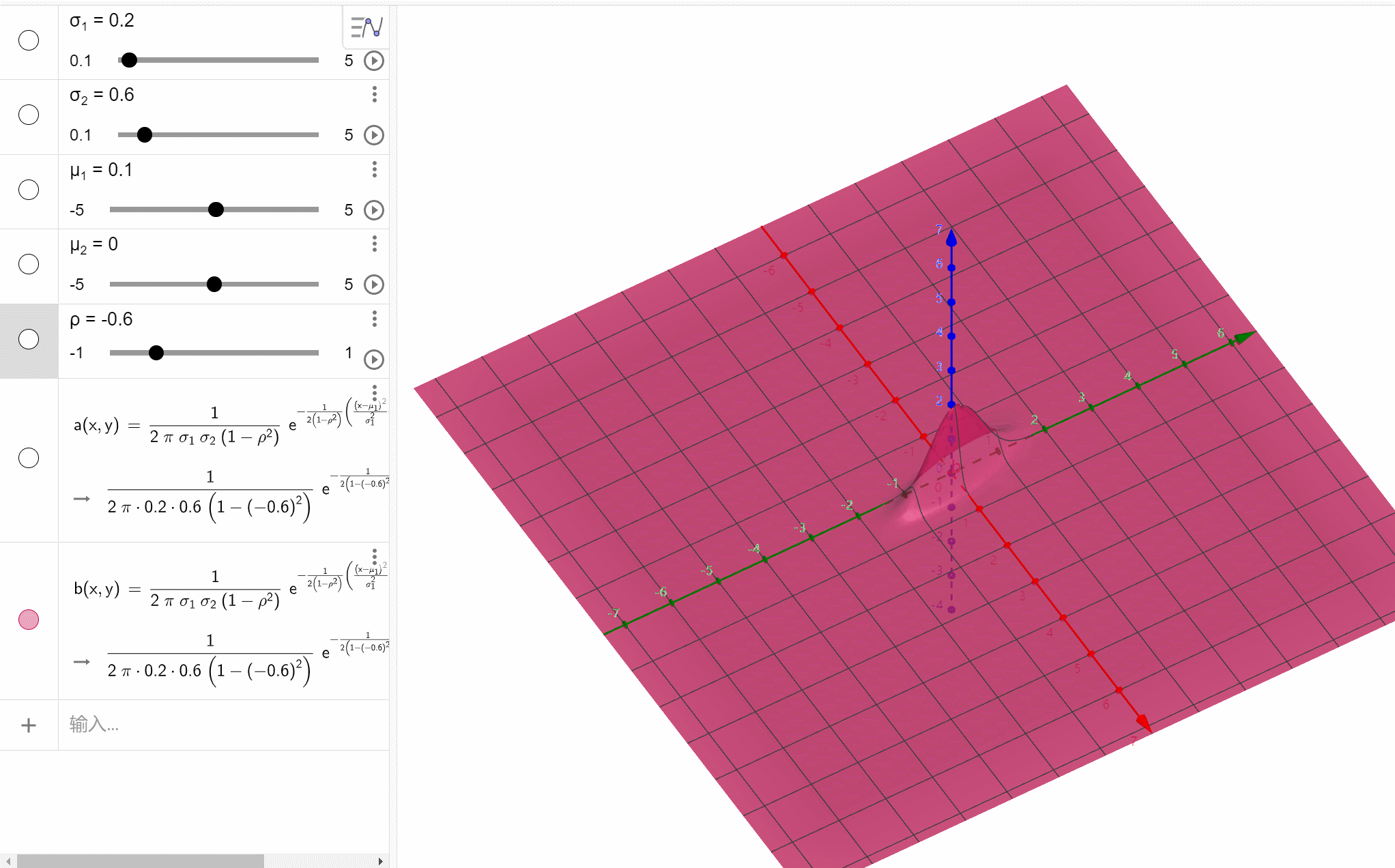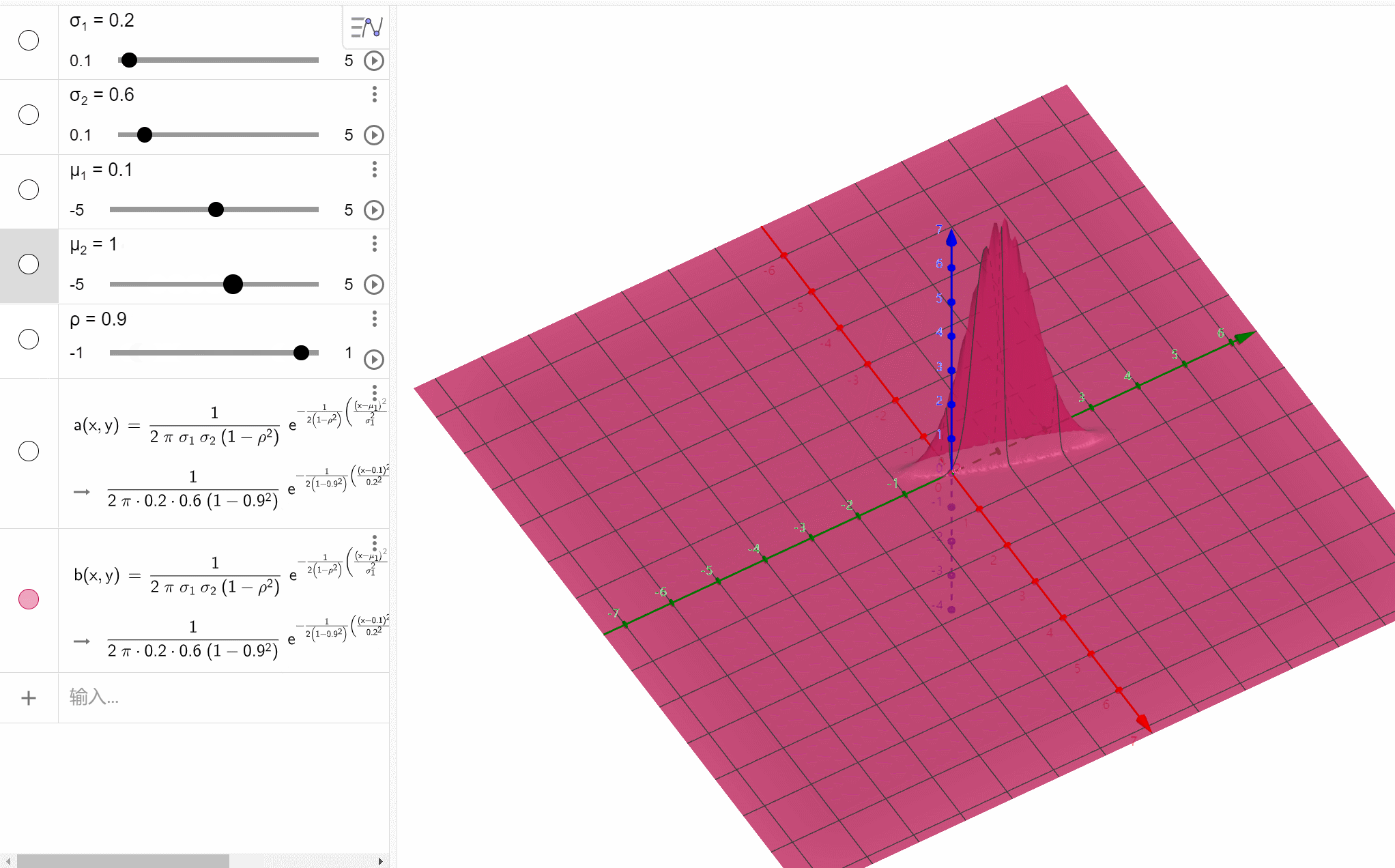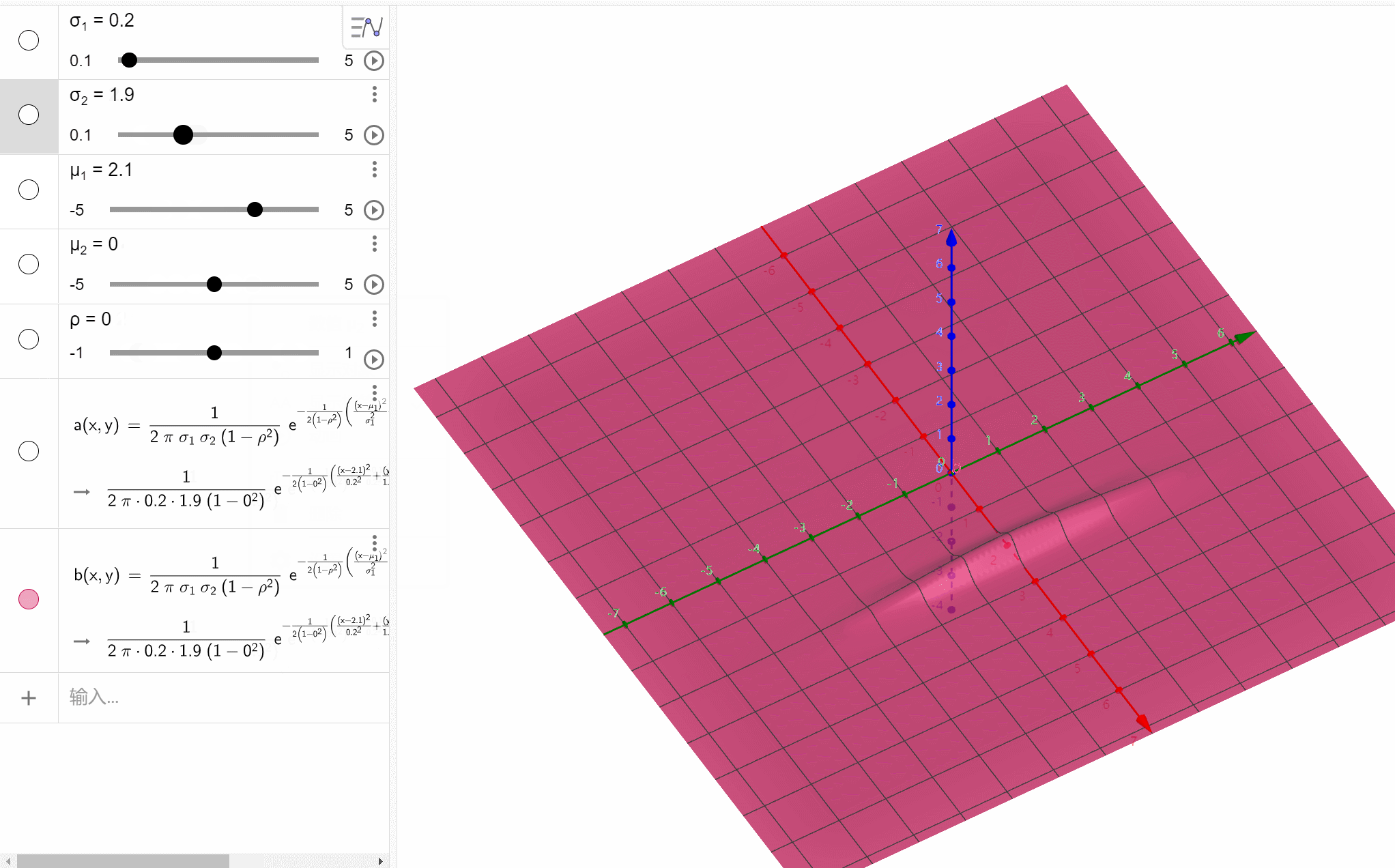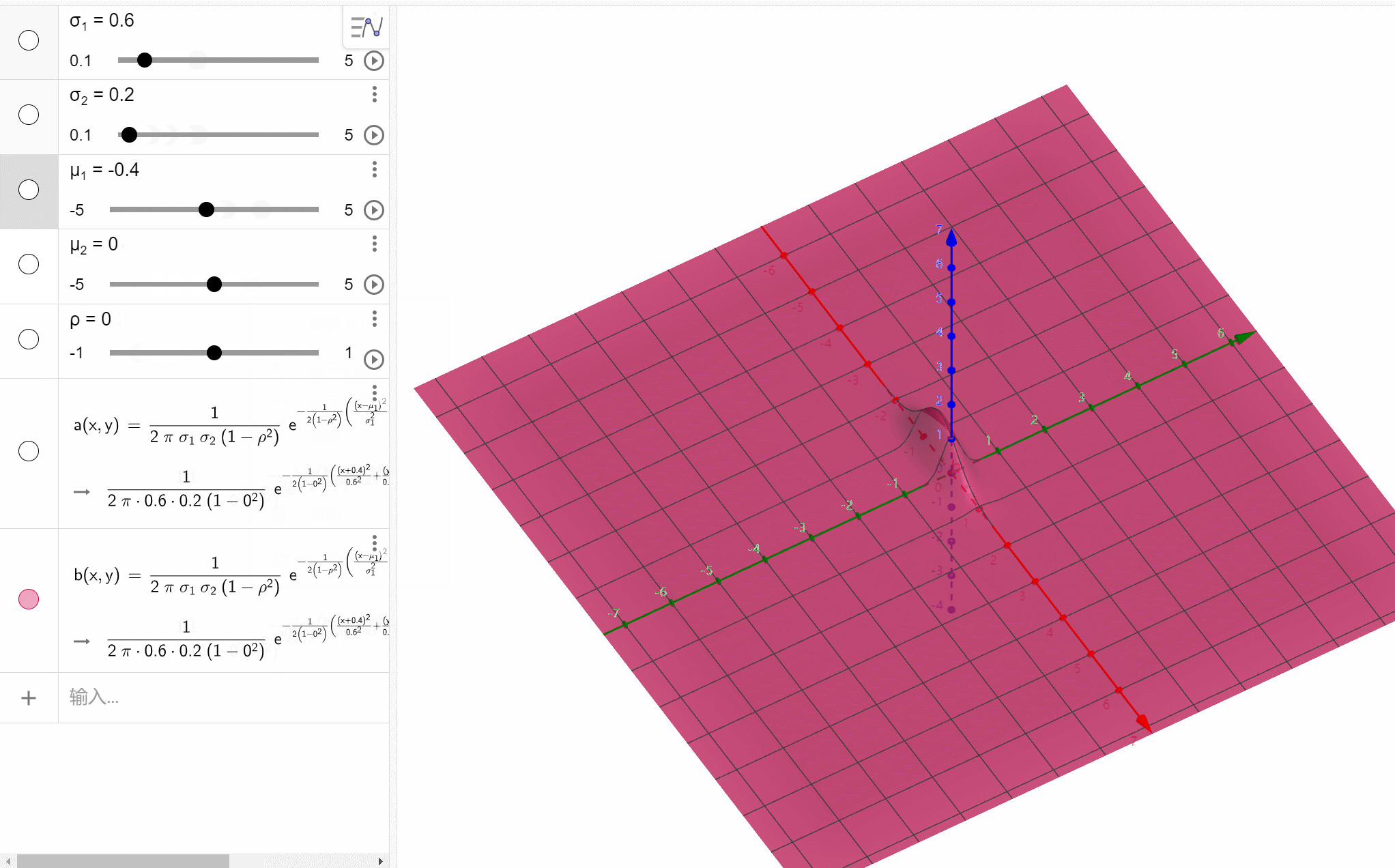
f(x,y)=2πσ1σ21−ρ21e−2(1−ρ2)1[σ12(x−μ1)2−2ρσ1σ2(x−μ1)(y−μ2)+σ22(y−μ2)2],x,y∈R函数图像:





![[JSON] JSON基础知识](https://img-blog.csdnimg.cn/294f60509d64456397f5f09112c09c3a.png)