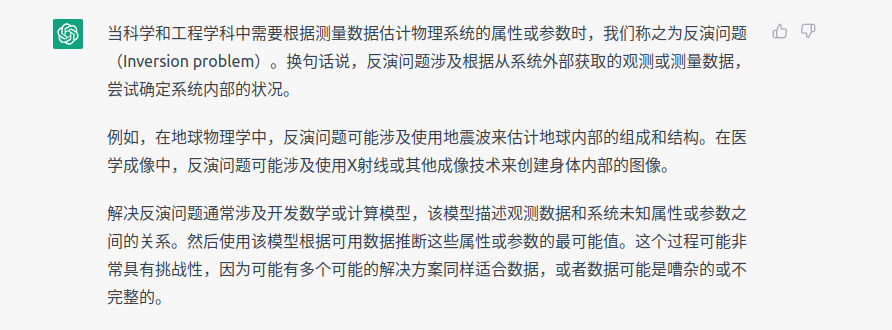
MMPBSA结合自由能计算原理
计算结合自由能的方法有很多,例如,热力学积分(Thermodynamic Integration,TI)、自由能微扰(Free Energy Perturbation,FEP)、MM/PB(GB)SA、线性相互作用能(Linear Interaction Energy,LIE)。MM/PB(GB)SA方法是精度和速度折衷的方法,广泛应用于受体-配体结合自由能计算。该方法全称 分子力学/泊松-波尔兹曼(广义波恩)表面积(Molecular Mechanics / Poisson Boltzmann (Generalized Born) Surface Area)。
基本原理
根据热力学的知识,自由能可以分解成焓和熵贡献的能量
G
=
H
−
T
S
G = H-TS
G=H−TS
焓是在某一环境中凭空变出某个物质所需的能量,如果是在真空中,那就等价于内能。所以对于溶液体系,上式的可以进一步分解,得到
G
=
U
+
G
s
o
l
−
T
S
G=U+G_{sol}-TS
G=U+Gsol−TS
式中,
U
U
U是内能,
G
s
o
l
G_{sol}
Gsol是溶剂化能,
S
S
S是溶液体系的熵。
气相溶质内能
是溶质处于真空中的内能,通常也就是指气相溶质的分子力学能量:
U
=
E
i
n
t
+
E
e
l
e
+
E
v
d
W
U=E_{int}+E_{ele}+E_{vdW}
U=Eint+Eele+EvdW
其中,
E
i
n
t
E_{int}
Eint是分子内部的能量,包括键长、键角、二面角不同引起的能量变化;
E
e
l
e
E_{ele}
Eele是静电能量;
E
v
d
w
E_{vdw}
Evdw是范德华能量。
溶剂化能
G s o l G_{sol} Gsol是溶剂化能,它包含了溶质进入溶剂的内能和熵的变化,以及排开溶剂所需要做的功。要准确地解释溶剂效应,则必须在模拟时显式地包含所有的溶剂分子,这需要极大的计算消耗。为了解决这个问题,过去的研究者们选择了隐式地引入溶质-溶剂相互作用。
其溶剂化能的完整形式可写作:
G
s
o
l
=
G
e
l
e
+
G
d
i
s
+
G
r
e
p
+
G
c
a
v
+
G
t
h
e
+
P
Δ
V
G_{sol}=G_{ele}+G_{dis}+G_{rep}+G_{cav}+G_{the}+P \Delta{V}
Gsol=Gele+Gdis+Grep+Gcav+Gthe+PΔV
其中,
G
e
l
e
G_{ele}
Gele是静电贡献;
G
d
i
s
G_{dis}
Gdis是色散能,反映范德华相互作用;
G
r
e
s
G_{res}
Gres是排斥能,表示由泡利不相容原理引起的短程相互作用;
G
c
a
v
G_{cav}
Gcav是成穴能,即形成空腔所需的能量;
G
t
h
e
G_{the}
Gthe热能项,解释了溶质振动和转动的变化;
显然
G
s
o
l
G_{sol}
Gsol可以分为极性(静电)极性部分和非极性贡献部分:
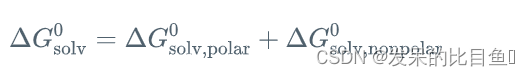
对于前者计算比较复杂,对于后者,计算较为简单,它正比于 溶剂可及表面积(solvent-accessible surface area,SASA),它体现了疏水效应,常用的表达式为:
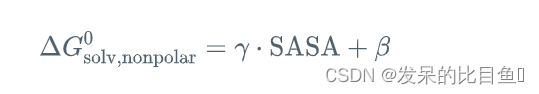
MM/PB(GB)SA
MM/PB(GB)SA基本原理是:计算两个溶剂化分子在结合(bound)和游离(unbound)状态的结合自由能之差或者比较同一个分子不同的溶剂化构象的自由能。按照下图所示的过程直接计算结合自由能,即可分别计算受体、配体以及它们的复合物各自在溶液中的能量,然后算差值:
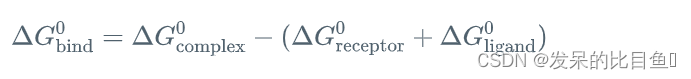
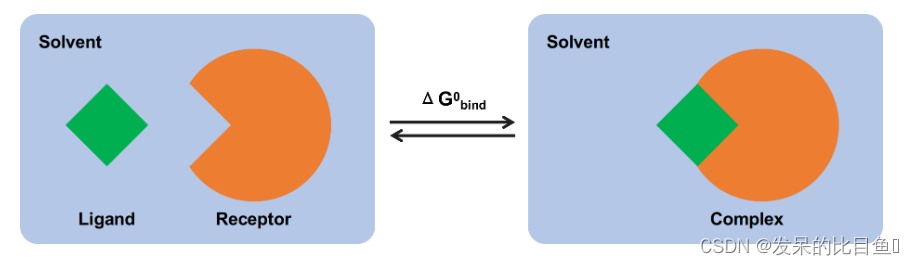
但在实际计算中,会遇到一个很严重的问题——能量贡献主要来自溶液间相互作用,并且总能量的波动幅度远大于结合能,这样就需要非常长的时间才能收敛。
为此,通过下面的热力学循环,“绕个弯”来避免这种糟糕的情况:

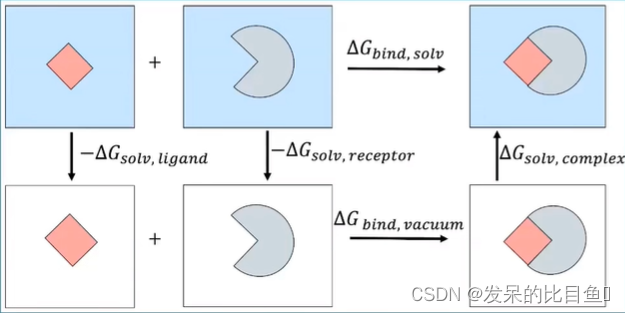
这个方案的含义是,将溶剂中的总结合自由能分拆成分子力学项(真空中的结合自由能)和溶剂化能两部分分别计算。
示例
下载李继存老师的gmx_mmpbsa的bash文件: https://github.com/Jerkwin/gmxtool/tree/master/gmx_mmpbsa
下载APBSA软件(我用的是APBS3.0):https://github.com/Electrostatics/apbs/releases
参考
https://zhuanlan.zhihu.com/p/469647067
https://zhuanlan.zhihu.com/p/352804973
https://zhuanlan.zhihu.com/p/379721714