AcWing 1015. 摘花生

Hello Kitty想摘点花生送给她喜欢的米老鼠。

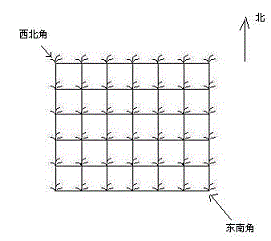
她来到一片有网格状道路的矩形花生地(如下图)，从西北角进去，东南角出来。

地里每个道路的交叉点上都有种着一株花生苗，上面有若干颗花生，经过一株花生苗就能摘走该它上面所有的花生。

Hello Kitty只能向东或向南走，不能向西或向北走。

问Hello Kitty最多能够摘到多少颗花生。

输入格式

第一行是一个整数T，代表一共有多少组数据。

接下来是T组数据。

每组数据的第一行是两个整数，分别代表花生苗的行数R和列数 C。

每组数据的接下来R行数据，从北向南依次描述每行花生苗的情况。每行数据有C个整数，按从西向东的顺序描述了该行每株花生苗上的花生数目M。

输出格式

对每组输入数据，输出一行，内容为Hello Kitty能摘到得最多的花生颗数。

数据范围

1≤T≤1001≤�≤100,

1≤R,C≤1001≤�,�≤100,

0≤M≤10000≤�≤1000

输入样例：

2
2 2
1 1
3 4
2 3
2 3 4
1 6 5

输出样例：

8
16

采用闫氏dp分析法。

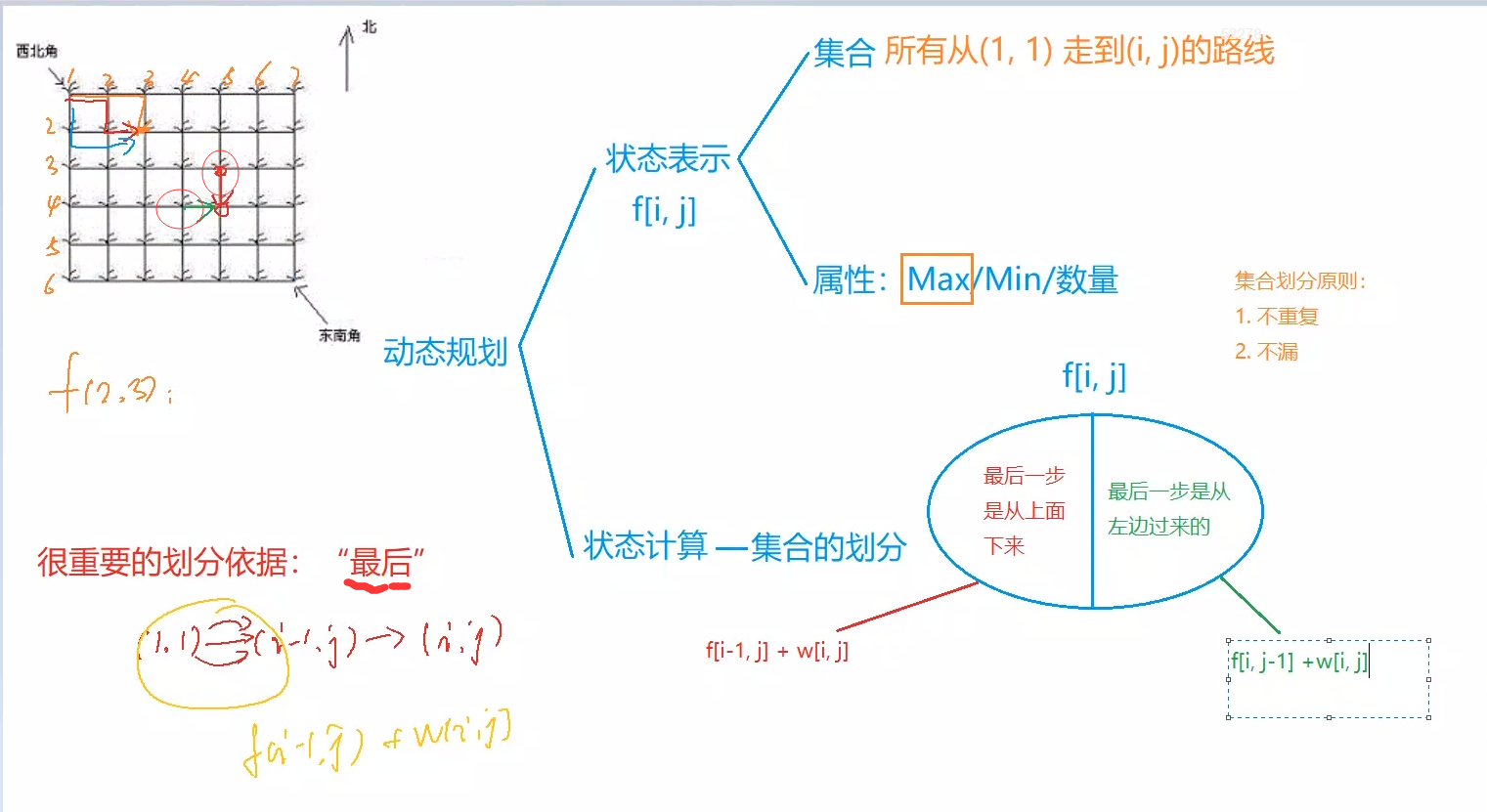
按照y总所说、各类DP问题、分别从两个方面去考虑、1：状态表示，2：状态划分。借用集合的思想、对这个题目进行分析、那本题要求的正是从左上角（1，1）到右下角（i，j）的路线中、花生数最大的那一条。状态表示一般还有一个方面就是属性、题目大多要求的是Max/Min/数量...那么、状态如何划分的呢？y总说状态划分这东西不是凭空捏造出来的、是你积累的题目中见的多了、自然而然就知道如何去解决了。有两个方面、不重复、不遗漏。可以发现、本题路线一共有两种、一种是从上面下来的、第二种是从左边过来的、那么我们就可以根据这个特点进行状态划分。

分析的时候有点难度、不过输出的时候答案就简单了、我们所要求的不正是开始输入的那个n和m么

状态转移方程也就是：

f[i][j] = max(f[i - 1][j], f[i][j - 1]) + w;

AC代码如下：

#include <bits/stdc++.h>
using namespace std;
int f[110][110], a[110][110];
int max(int a, int b)
{
    return a > b ? a : b;
}
int main()
{
    int t, r, c, i, j;
    scanf("%d", &t);
    while(t--)
    {
        memset(f, 0, sizeof(f));
        scanf("%d%d", &r, &c);
        for(i = 1; i <= r; i++)
            for(j = 1; j <= c; j++)
                scanf("%d", &a[i][j]);
        for(i = 1; i <= r; i++)
            for(j = 1; j <= c; j++)
                f[i][j] = max(f[i - 1][j], f[i][j - 1]) + a[i][j];
        printf("%d\n", f[r][c]);
    }
    return 0;
}