paper：Relational Knowledge Distillation

code：https://github.com/megvii-research/mdistiller/blob/master/mdistiller/distillers/RKD.py

背景

本文从语言结构主义的角度来重新审视知识蒸馏，前者主要关注一个符号学系统中的结构关系。索续尔关于符号关系身份的概念是结构主义理论的核心：“在一种语言中，和在其他符号系统中一样，区分一个符号的依据是构成它的要素（what distinguishes a sign is what constitutes it）。从这个角度来看，一个符号的意义取决于它与系统内其他符号的关系，一个符号没有独立于上下文的绝对意义。

本文的创新点

本文的中心思想是：相比于学习到的单个特征表示，用学习到的特征表示之间的关系（relation）作为知识是更好的选择。单个数据比如一张图像，在一个表示系统中获得了与其它数据相关联的特征表示，因此主要的信息包含在数据嵌入空间中的一个结构中的。基于此，本文引入了一种新的知识蒸馏方法，称为关系知识蒸馏（Relational Knowledge Distillation, RKD），他传递的是输出之间的结构关系而不是单个输出本身，如下图所示

具体来说，提出了两种RKD损失：基于距离的二阶（distance-wise, second-order）和基于角度的三阶（angle-wise, third-order）蒸馏损失，RKD可以看作是传统KD的一种泛化，由于其和传统KD的互补性，也可以与其它方法结合使用来提高模型性能。

方法介绍

对于一个教师模型 \(T\) 和一个学生模型 \(S\)，\(f_{T}\) 和 \(f_{S}\) 分别表示教师和学生模型的函数。通常这些模型是深度神经网络，原则上函数 \(f\) 可以用网络任何层的输出来定义（比如隐藏层或softmax层）。\(\mathcal{X}^{N}\) 表示一组数据中的 \(N\) 个不同样本的元组，例如 \(\mathcal{X}^2=\left \{ \left ( x_{i},x_{j}|i\ne j \right ) \right \} \)，\(\mathcal{X}^3=\left \{ \left ( x_{i},x_{j},x_{k}|i\ne j\ne k \right ) \right \} \)。RKD旨在使用教师模型输出表示中数据实例之间的相互关系来传递结构性知识，和传统方法不同，它计算所有数据中每 \(n\) 个样本子集的关系势（relation potential）\(\psi\)，并且通过势将信息从教师模型传递给学生模型。

定义 \(t_{i}=f_{T}(x_{i})\)，\(s_{i}=f_{S}(x_{i})\)，RKD的目标损失如下

其中 \((x_{1},x_{2},...,x_{n})\) 是 \(\mathcal{X}^{N}\) 中的一个 \(n\) 元素的子集，\(\psi\) 是一个关系势函数用来计算给定 \(n\) 个样本子集的关系势能（relational energy），\(l\) 是用来惩罚教师和学生模型之间差异的损失函数。当关系是一元时，式(4)的RKD就变成了IKD（即传统的Individual KD），下图是RKD和IKD的对比

关系势函数 \(\psi\) 在RKD中起着至关重要的作用，RKD的有效性和效率依赖于势函数的选择。例如高阶（high-order）势在捕获高阶结构方面更有效但计算复杂度也更高。本文作者提出了两种简单有效的势函数和对应RKD损失：distance-wise和angle-wise损失，它们分别样本之间的二元关系（pairwise）和三元关系（ternary）。

Distance-wise distillation loss

给定两个训练样本，distance-wise势函数 \(\psi_{D}\) 计算输出表示空间中两者之间的欧式距离

其中 \(\mu\) 是距离的标准化因子，为了关注其它样本对之间的相对距离，\(\mu\) 设置为mini-batch中来自 \(\mathcal{X}^{2}\) 的所有样本对的平均距离

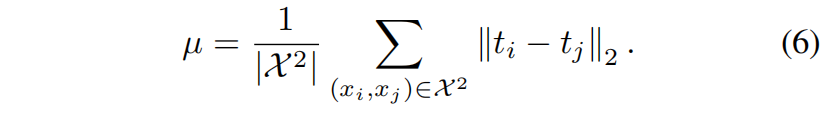
利用在教师模型和学生模型中分别计算的distance-wise potentials，distance-wise蒸馏损失定义如下

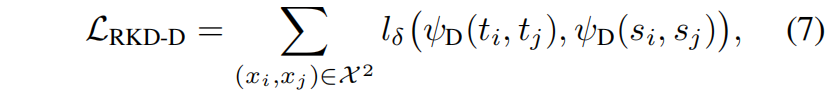
其中 \(l_{\delta}\) 是Hube loss，定义如下

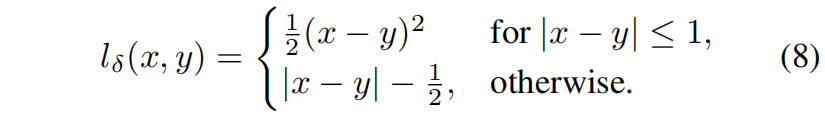
距离蒸馏损失通过惩罚样本输出表示空间之间的距离差来传递样本之间的关系，与传统的KD不同，它不是让学生模型去匹配教师模型的输出，而是让学生模型关注输出的距离结构。

Angle-wise distillation loss

给定三个样本，基于角度的势函数计算输出表示空间中三个样本之间的角度

利用分别在教师模型和学生模型中计算的angle-wise potentials，基于角度的蒸馏损失定义如下

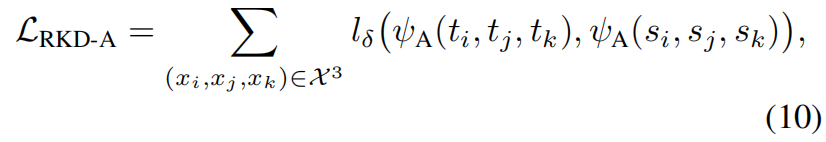
其中 \(l_{\delta}\) 是Hube loss，基于角度的蒸馏损失通过惩罚角度差异来传递训练样本之间的关系。由于角度是比距离更高阶（high-order）的属性，它可能更有效地传递关系信息，在训练中给学生模型更大的灵活性。作者在实验中也发现基于角度的损失收敛更快性能更好。

Training with RKD

训练过程中多个蒸馏损失包括本文提出的RKD可以单独使用，也可以和任务特定的损失结合使用，例如分类任务中的交叉熵损失。因此完整的损失形式如下

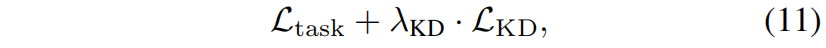
其中 \(\mathcal{L}_{task}\) 是特定任务相关的损失，\(\mathcal{L}_{KD}\) 是蒸馏损失，\(\lambda_{KD}\) 是权重超参。

代码解析

其中输入特征feature_student["pooled_feat"]是网络最后全连接层的输入，也就是最后一层卷积层的输出进行全局平局池化再reshape成 (batch_size, -1)的结果。函数_pdist计算样本输出特征之间的欧式距离，res = (e_square.unsqueeze(1) + e_square.unsqueeze(0) - 2 * prod).clamp(min=eps)是将 \((a-b)^2\) 展开成 \(a^{2}+b^{2}-2ab\)。40-41行计算式(9)中的 \(\mathbf{e}^{ij}\) 和 \(\mathbf{e}^{kj}\)，\(\left \langle \cdot \right \rangle \) 是点积操作，42行是计算 \(\left \langle \mathbf{e}^{ij},\mathbf{e}^{kj} \right \rangle \)。

import torch
import torch.nn as nn
import torch.nn.functional as F

from ._base import Distiller


def _pdist(e, squared, eps):
    e_square = e.pow(2).sum(dim=1)  # (64,256)->(64)
    prod = e @ e.t()  # (64,64)
    res = (e_square.unsqueeze(1) + e_square.unsqueeze(0) - 2 * prod).clamp(min=eps)
    # (64,1)+(1,64)->(64,64), -(64,64)->(64,64)

    if not squared:
        res = res.sqrt()

    res = res.clone()
    res[range(len(e)), range(len(e))] = 0
    return res


def rkd_loss(f_s, f_t, squared=False, eps=1e-12, distance_weight=25, angle_weight=50):
    stu = f_s.view(f_s.shape[0], -1)  # (64,256)->(64,256)
    tea = f_t.view(f_t.shape[0], -1)  # (64,256)->(64,256)

    # RKD distance loss
    with torch.no_grad():
        t_d = _pdist(tea, squared, eps)
        mean_td = t_d[t_d > 0].mean()
        t_d = t_d / mean_td

    d = _pdist(stu, squared, eps)
    mean_d = d[d > 0].mean()
    d = d / mean_d

    loss_d = F.smooth_l1_loss(d, t_d)

    # RKD Angle loss
    with torch.no_grad():
        td = tea.unsqueeze(0) - tea.unsqueeze(1)  # (1,64,256)-(64,1,256)->(64,64,256)
        norm_td = F.normalize(td, p=2, dim=2)  # (64,64,256)
        t_angle = torch.bmm(norm_td, norm_td.transpose(1, 2)).view(-1)  # (64,64,256),(64,256,64)->(64,64,64)->(262144)

    sd = stu.unsqueeze(0) - stu.unsqueeze(1)
    norm_sd = F.normalize(sd, p=2, dim=2)
    s_angle = torch.bmm(norm_sd, norm_sd.transpose(1, 2)).view(-1)

    loss_a = F.smooth_l1_loss(s_angle, t_angle)

    loss = distance_weight * loss_d + angle_weight * loss_a
    return loss


class RKD(Distiller):
    """Relational Knowledge Disitllation, CVPR2019"""

    def __init__(self, student, teacher, cfg):
        super(RKD, self).__init__(student, teacher)
        self.distance_weight = cfg.RKD.DISTANCE_WEIGHT
        self.angle_weight = cfg.RKD.ANGLE_WEIGHT
        self.ce_loss_weight = cfg.RKD.LOSS.CE_WEIGHT
        self.feat_loss_weight = cfg.RKD.LOSS.FEAT_WEIGHT
        self.eps = cfg.RKD.PDIST.EPSILON
        self.squared = cfg.RKD.PDIST.SQUARED

    def forward_train(self, image, target, **kwargs):
        logits_student, feature_student = self.student(image)  # (64,3,32,32)
        with torch.no_grad():
            _, feature_teacher = self.teacher(image)

        # losses
        loss_ce = self.ce_loss_weight * F.cross_entropy(logits_student, target)
        loss_rkd = self.feat_loss_weight * rkd_loss(
            feature_student["pooled_feat"],  # (64,256)
            feature_teacher["pooled_feat"],  # (64,256)
            self.squared,  # False
            self.eps,  # 1e-12
            self.distance_weight,  # 25
            self.angle_weight,  # 50
        )
        losses_dict = {
            "loss_ce": loss_ce,
            "loss_kd": loss_rkd,
        }
        return logits_student, losses_dict