文章目录
- 约束优化:约束优化的三种序列无约束优化方法
- 外点罚函数法
- L2-罚函数法:非精确算法
- 对于等式约束
- 对于不等式约束
- L1-罚函数法:精确算法
- 内点罚函数法:障碍函数法
- 等式约束优化问题的拉格朗日函数法:Uzawa's Method for convex optimization
- 参考文献
约束优化:约束优化的三种序列无约束优化方法
罚函数法是指将约束作为惩罚项加到目标函数中,从而转化成熟悉的无约束优化问题。
外点罚函数法
简而言之,外点罚函数法是指对于可行域外的点,惩罚项为正,即对该点进行惩罚;对于可行域内的点,惩罚项为0,即不做任何惩罚。因此,该算法在迭代过程中点列一般处于可行域之外,惩罚项会促使无约束优化问题的解落在可行域内。罚函数一般由约束部分乘正系数组成,通过增大该系数,我们可以更严厉地惩罚违反约束的行为,从而迫使惩罚函数的最小值更接近约束问题的可行区域。
L2-罚函数法:非精确算法
对于等式约束


对于不等式约束


对于一般优化问题,则是将上述不等式约束和等式约束的惩罚项加到一起。

什么情况下使用L2-罚函数法?
- 实际优化问题中,等式与不等式约束具有物理意义;
- 约束违背量不要求特别小,在1e-2~1e-3之间可接受就行。例如某优化问题中速度约束 v ≤ 10 v \leq 10 v≤10,解 v = 10.01 v=10.01 v=10.01也可以接受。
使用该方法时,可采用如下两种方式:
- 一步到位,即取 σ \sigma σ足够大,直接解无约束罚函数P最优化问题,此时P最优解是个近似解,与实际最优解之间的误差在可接受范围内;
- 序列迭代优化,例如:
σ = 1 ⟹ P ( x , 1 ) \sigma=1 \implies P(x,1) σ=1⟹P(x,1),解 x 1 ∗ = x 1 x^{*}_{1}=x_1 x1∗=x1;
σ = 10 ⟹ P ( x , 10 ) \sigma=10 \implies P(x,10) σ=10⟹P(x,10),上一次迭代 x 1 x_1 x1作初值解 x 2 ∗ = x 2 x^{*}_{2}=x_2 x2∗=x2;
σ = 100 ⟹ P ( x , 100 ) \sigma=100 \implies P(x,100) σ=100⟹P(x,100),上一次迭代 x 2 x_2 x2作初值解 x 3 ∗ = x 3 x^{*}_{3}=x_3 x3∗=x3;
……直到达到收敛准则。算法伪代码如下:

一般情况下,具体选择何种方式取决于实际工程问题的精度需求和速度需求。
L2-罚函数法的优缺点?
优点:
- 将约束优化问题转化为无约束优化问题,当 c i ( x ) c_i(x) ci(x)光滑时可以调用一般的无约束光滑优化问题算法求解;
- 二次罚函数形式简洁直观而在实际中广泛使用。
缺点:
- 需要 σ → ∞ \sigma \rightarrow \infty σ→∞,此时海瑟矩阵条件数过大,对于无约束优化问题的数值方法拟牛顿法与共轭梯度法存在数值困难,且需要多次迭代求解子问题;
- 对于存在不等式约束的 P ( x , σ ) P(x,\sigma) P(x,σ)可能不存在二次可微性质,光滑性降低;
- 不精确,与原问题最优解存在距离。
例子:
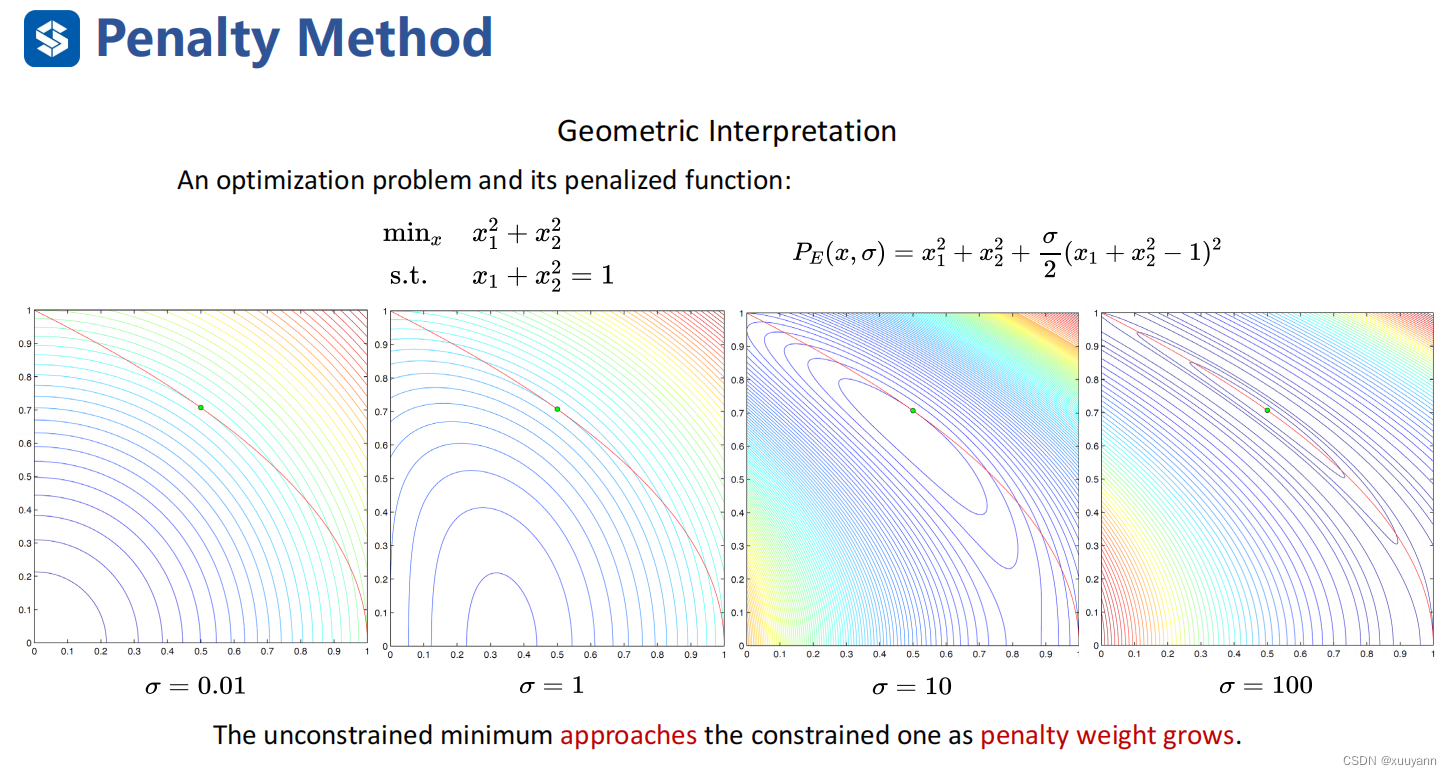
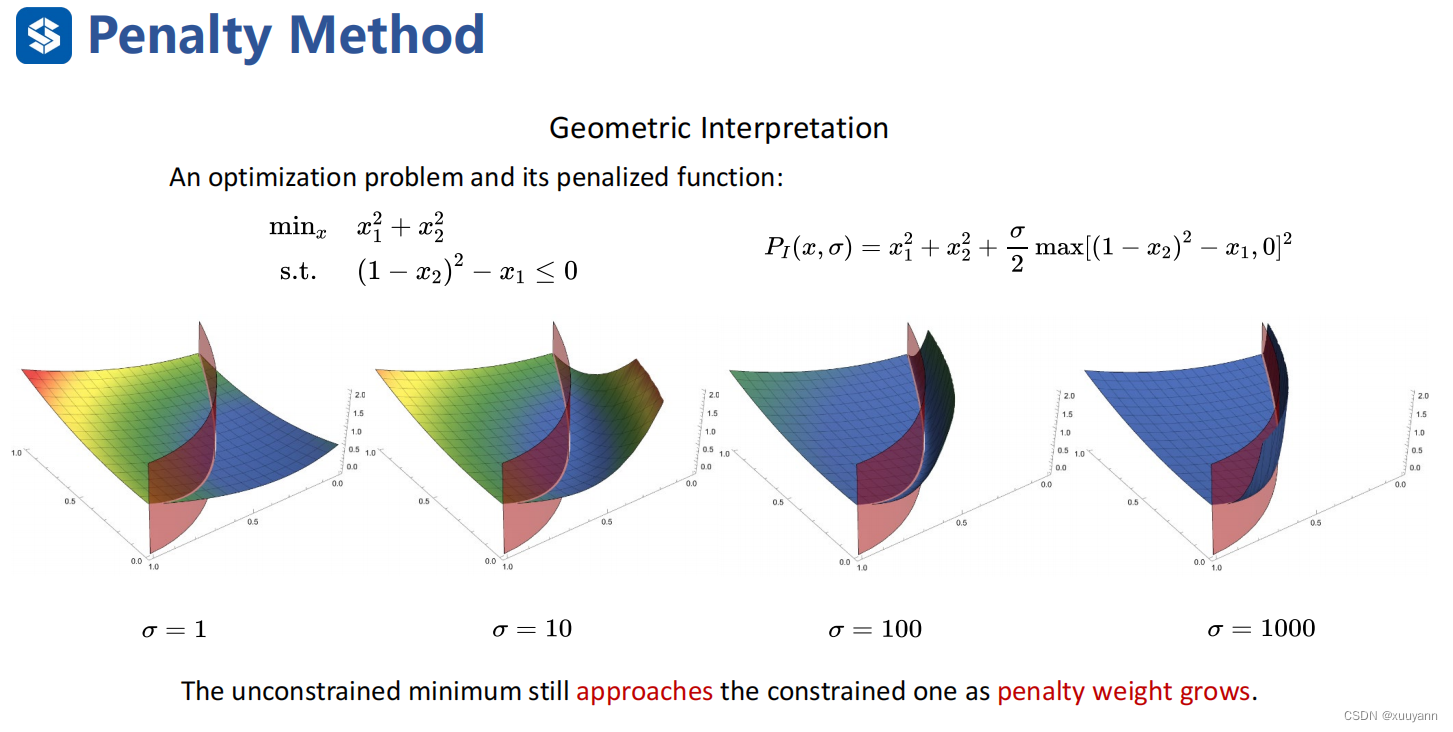
L1-罚函数法:精确算法
由于L2-罚函数法存在数值困难,并且与原问题的解存在误差,因此考虑精确罚函数法。精确罚函数是一种问题求解时不需要令罚因子趋于正无穷(或零)的罚函数。换句话说,若罚因子选取适当,对罚函数进行极小化得到的解恰好就是原问题的精确解。这个性质在设计算法时非常有用,使用精确罚函数的算法通常会有比较好的性质。
由于L1-罚函数非光滑,因此无约束优化问题P的收敛速度无法保证,这实际上就相当于用牺牲收敛速度的方式来换取优化问题P的精确最优解。

内点罚函数法:障碍函数法
前面介绍的L1和L2罚函数均属于外点罚函数,即在求解过程中允许自变量 x x x位于原问题可行域之外,当罚因子趋于无穷时,子问题最优解序列从可行域外部逼近最优解。自然地,如果我们想要使得子问题最优解序列从可行域内部逼近最优解,则需要构造内点罚函数。顾名思义,内点罚函数在迭代时始终要求自变量 x x x不能违反约束,因此它主要用于不等式约束优化问题。
如下图所示,考虑含不等式约束的优化问题,为了使迭代点始终在可行域内,当迭代点趋于可行域边界时,我们需要罚函数趋于正无穷。常见的罚函数有三种:对数罚函数,逆罚函数和指数罚函数。对于原问题,它的最优解通常位于可行域边界,即 c i ( x ) ≤ 0 c_i(x) \leq 0 ci(x)≤0中至少有一个取到等号,此时需要调整惩罚因子 σ \sigma σ使其趋于0,这会减弱障碍罚函数在边界附近的惩罚效果。

算法伪代码如下:

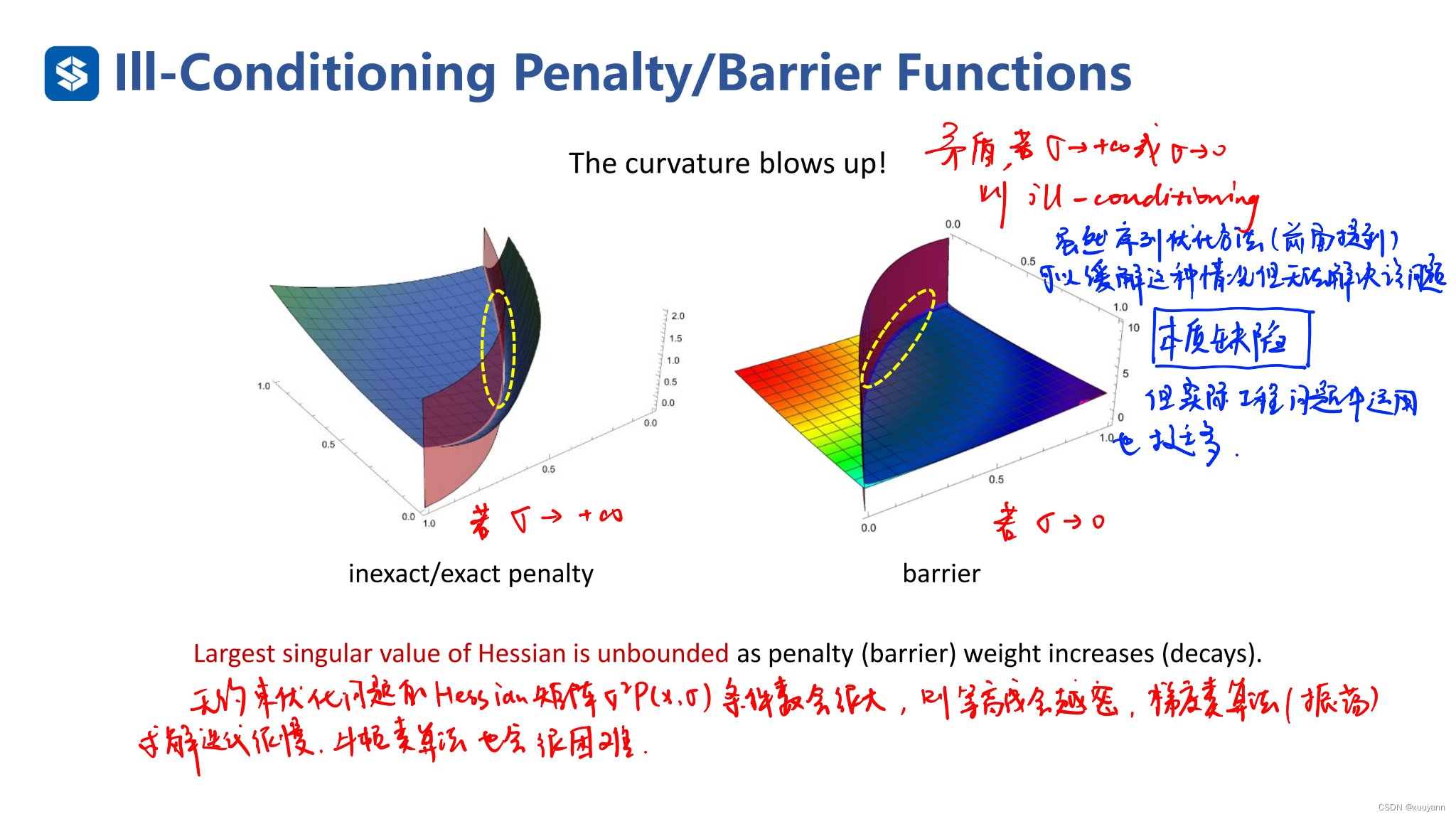
同样地,内点罚函数法也会有类似外点罚函数法的数值困难,即当 σ \sigma σ趋于0时,子问题 P ( x , σ ) P(x,\sigma) P(x,σ)的海瑟矩阵条件数会趋于无穷,因此对子问题的求解将会越来越困难。
等式约束优化问题的拉格朗日函数法:Uzawa’s Method for convex optimization
基础预备:
凸优化学习笔记(一)
凸优化学习笔记:Lagrange函数、对偶函数、对偶问题、KKT条件
多元函数的极值和鞍点
**若原问题是凸问题,则KKT条件是充要条件。**原问题连续凸则拉格朗日函数严格凸,原问题的最优值 p ∗ p^* p∗与对偶问题的最优值 d ∗ d^* d∗相等, ( x ∗ , λ ∗ ) (x^*,\lambda ^*) (x∗,λ∗)是拉格朗日函数的鞍点,同时也是原问题和对偶问题的最优解。


综上分析,Uzawa’s Method迭代过程分为两个步骤:
{
x
k
+
1
=
argmin
x
L
(
x
,
λ
k
)
λ
k
+
1
=
λ
k
+
α
(
A
x
k
+
1
−
b
)
\left\{\begin{array}{l} x^{k+1}=\underset{x}{\operatorname{argmin}} \mathcal{L}\left(x, \lambda^k\right) \\ \lambda^{k+1}=\lambda^k+\alpha\left(A x^{k+1}-b\right) \end{array}\right.
{xk+1=xargminL(x,λk)λk+1=λk+α(Axk+1−b)
(1)给定
λ
k
\lambda^k
λk,求解
min
x
L
(
x
,
λ
k
)
\min _x \mathcal{L}(x, \lambda^k)
minxL(x,λk)无约束优化问题,求解得到
x
k
+
1
x^{k+1}
xk+1;
(2)更新 λ \lambda λ, L ( x k + 1 , λ ) L(x^{k+1},\lambda) L(xk+1,λ)关于 λ \lambda λ的梯度为 ∂ L ∂ λ ∣ x + 1 = A x k + 1 − b \left.\frac{\partial L}{\partial \lambda}\right|_{x+1}=A x^{k+1}-b ∂λ∂L x+1=Axk+1−b,若要求解 max λ L ( x k + 1 , λ ) \max _\lambda \mathcal{L}(x^{k+1}, \lambda) maxλL(xk+1,λ),则沿着梯度上升方向进入步长迭代,即 λ k + 1 = λ k + α ( A x k + 1 − b ) \lambda^{k+1}=\lambda^k+\alpha\left(A x^{k+1}-b\right) λk+1=λk+α(Axk+1−b), α \alpha α为迭代步长。
该方法的前提就是原函数连续凸, L ( x , λ ) \mathcal L(x,\lambda) L(x,λ)关于 x x x严格凸,则 min x L ( x , λ k ) \min _x \mathcal{L}(x, \lambda^k) minxL(x,λk)只存在一个最优解,可求出唯一 x k + 1 x^{k+1} xk+1进而更新 λ k + 1 \lambda^{k+1} λk+1,否则 x k + 1 x^{k+1} xk+1会存在多个,不知道选择哪个去更新 λ \lambda λ。因此缺点很明显,该方法要求原函数必须为连续凸函数,梯度上升步长需要调整且收敛速率不能保证。
参考文献
机器人中的数值优化
最优化:建模、算法与理论/最优化计算方法