吾日三省吾身:高否?富否?帅否?答曰:否。滚去学习!!!(看完这篇文章先)
目前只有C和C++的功底,暂时还未开启新语言的学习,但是大同小异,语法都差不多。
目录:
一.排序定义
二.排序算法的评价指标(最后总结)
1.算法的稳定性
2.时间复杂度和空间复杂度
三.七大排序算法
1.冒泡排序
2.选择排序
3.插入排序
4.希尔排序
5.归并排序
6.快速排序
7.堆排序
稳定性及其复杂度总结
一.排序定义
排序(sort):排序就是重新排列表中的元素,使得元素满足按关键字有序的过程。
二.排序算法的评价指标(最后总结)
1.算法的稳定性
若待排序表中有两个元素R1和R2,其对应的关键字相同即k1= k2,且在排序前R1在R2的前面,若使用某一排序算法排序后,R1仍然在R2的前面,则称这个排序算法是稳定的,否则称排序算法是不稳定的。
意思就是两个相同的关键字在排序前后位置不变,排序前在前面那么排序前就在前面,后面就在后面。
如果排序前后两个数的位置不相同,那么此算法就是不稳定的。
2.时间复杂度和空间复杂度
三.七大排序算法
·排序算法分为内部排序和外部排序,内部排序的时候哦数据都存储在内存中,外部排序中由于数据过多而无法全部放入内存。
冒泡排序

冒泡排序(Bubble Sort)也是一种简单直观的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢"浮"到数列的顶端。冒泡排序还有一种优化算法,就是立一个 flag,当在一趟序列遍历中元素没有发生交换,则证明该序列已经有序。
冒泡排序算法步骤:
从数组的第一个元素开始,依次比较每对相邻的元素,如果前面的元素大于后面的元素,就交换它们的位置。
对数组中的每一对相邻元素重复步骤1,直到最后一个元素。此时,数组中最后一个元素应该是最大的元素。
针对除去已排序的最后一个元素的剩余元素,重复步骤1和步骤2,直到整个数组都被排序。
注意:
当输入的数据是正序这个时候排序最快
当输入的数据是反序这个时候排序最慢
C语言实现
#include <stdio.h>
void bubble_sort(int arr[], int len) {
int i, j, temp;
for (i = 0; i < len - 1; i++)
for (j = 0; j < len - 1 - i; j++)
if (arr[j] > arr[j + 1]) {
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
int main() {
int arr[] = { 2, 4, 6, 8, 5, 7,9 , 1,3,10};
int len = (int) sizeof(arr) / sizeof(*arr);
bubble_sort(arr, len);
int i;
for (i = 0; i < len; i++)
printf("%d ", arr[i]);
return 0;
}C++实现
#include <iostream>
using namespace std;
template<typename T> //整数或浮点数皆可使用,若要使用类(class)或结构体(struct)时必须重载大于(>)运算符
void bubble_sort(T arr[], int len) {
int i, j;
for (i = 0; i < len - 1; i++)
for (j = 0; j < len - 1 - i; j++)
if (arr[j] > arr[j + 1])
swap(arr[j], arr[j + 1]);
}
int main() {
int arr[] = {2, 4, 6, 8, 5, 7,9 , 1,3,10 };
int len = (int) sizeof(arr) / sizeof(*arr);
bubble_sort(arr, len);
for (int i = 0; i < len; i++)
cout << arr[i] << ' ';
cout << endl;
return 0;
}时间复杂度:最坏情况:O(N^2)
最好情况:O(N)
空间复杂度:O(1)
2.选择排序
选择排序(Selection Sort)是一种简单的排序算法。其基本思想是首先从未排序的元素中找到最小的元素,然后将其放到已排序的序列末尾,然后再从剩余未排序的元素中继续找到最小的元素,将其放到已排序的序列末尾,以此类推,直到所有元素都排好序。
选择排序的算法步骤
遍历待排序的数组,从第一个元素开始
在未排序的元素中找到最小的元素,记录其下标
将最小的元素与第一个元素交换位置
接着在未排序的元素中继续寻找最小的元素,记录其下标
将最小的元素与第二个元素交换位置
重复步骤 4-5 直到所有元素都排序完成
C语言实现
void swap(int *a,int *b) //交换两个数
{
int temp = *a;
*a = *b;
*b = temp;
}
void selection_sort(int arr[], int len)
{
int i,j;
for (i = 0 ; i < len - 1 ; i++)
{
int min = i;
for (j = i + 1; j < len; j++) //走访未排序的元素
if (arr[j] < arr[min]) //找到目前最小值
min = j; //记录最小值
swap(&arr[min], &arr[i]); //做交換
}
}C++实现
template<typename T>
void selection_sort(std::vector<T>& arr) {
for (int i = 0; i < arr.size() - 1; i++) {
int min = i;
for (int j = i + 1; j < arr.size(); j++)
if (arr[j] < arr[min])
min = j;
std::swap(arr[i], arr[min]);
}
}3.插入排序
插入排序(Insertion Sort)排序算法,其思想是从第二个元素开始依次将其插入到已经有序的序列中。
插入排序的算法步骤
1第二个元素开始,将该元素视为一个有序序列。
2将该元素与它前面的元素进行比较,如果前面的元素比它大,则交换位置。
3继续向前比较,直到该元素找到了合适的位置。
4对下一个元素重复上述过程,直到所有元素都排好序为止。
C语言实现
void insertion_sort(int arr[], int len){
int i,j,key;
for (i=1;i<len;i++){
key = arr[i];
j=i-1;
while((j>=0) && (arr[j]>key)) {
arr[j+1] = arr[j];
j--;
}
arr[j+1] = key;
}
}C++实现
void insertion_sort(int arr[],int len){
for(int i=1;i<len;i++){
int key=arr[i];
int j=i-1;
while((j>=0) && (key<arr[j])){
arr[j+1]=arr[j];
j--;
}
arr[j+1]=key;
}
}时间复杂度:最坏情况下为O(N*N),此时待排序列为逆序,或者说接近逆序
最好情况下为O(N),此时待排序列为升序,或者说接近升序。
空间复杂度:O(1)
4.希尔排序
希尔排序(Shell Sort)是插入排序的一种改进版本,也被称为“缩小增量排序”。它的基本思想是先将待排序的序列分割成若干个子序列,对每个子序列进行插入排序,然后逐步缩小子序列的长度,最终完成排序。
算法步骤
1.选择一个增量序列 t1,t2,……,tk,其中 ti > tj, t k = 1;
2.按增量序列个数 k,对序列进行 k 趟排序;
3.每趟排序,根据对应的增量 ti,将待排序列分割成若干长度为 m 的子序列,分别对各子表进行直接插 入排序。仅增量因子为 1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
C语言实现
void shell_sort(int arr[], int len) {
int gap, i, j;
int temp;
for (gap = len >> 1; gap > 0; gap >>= 1)
for (i = gap; i < len; i++) {
temp = arr[i];
for (j = i - gap; j >= 0 && arr[j] > temp; j -= gap)
arr[j + gap] = arr[j];
arr[j + gap] = temp;
}
}C++实现
template<typename T>
void shell_sort(T array[], int length) {
int h = 1;
while (h < length / 3) {
h = 3 * h + 1;
}
while (h >= 1) {
for (int i = h; i < length; i++) {
for (int j = i; j >= h && array[j] < array[j - h]; j -= h) {
std::swap(array[j], array[j - h]);
}
}
h = h / 3;
}
}时间复杂度平均:O(N^1.3)
空间复杂度:O(1)
5.归并排序
归并排序(Merge Sort)是一种分治算法,其基本思想是将待排序序列分成若干个子序列,分别进行排序,然后将子序列合并成一个有序序列。
归并排序算法步骤:
将待排序序列分成两个子序列,分别进行递归排序。
合并两个有序子序列,得到一个更长的有序序列。
重复上述过程,直到所有子序列都有序。
int min(int x, int y) {
return x < y ? x : y;
}
void merge_sort(int arr[], int len) {
int *a = arr;
int *b = (int *) malloc(len * sizeof(int));
int seg, start;
for (seg = 1; seg < len; seg += seg) {
for (start = 0; start < len; start += seg * 2) {
int low = start, mid = min(start + seg, len), high = min(start + seg * 2, len);
int k = low;
int start1 = low, end1 = mid;
int start2 = mid, end2 = high;
while (start1 < end1 && start2 < end2)
b[k++] = a[start1] < a[start2] ? a[start1++] : a[start2++];
while (start1 < end1)
b[k++] = a[start1++];
while (start2 < end2)
b[k++] = a[start2++];
}
int *temp = a;
a = b;
b = temp;
}
if (a != arr) {
int i;
for (i = 0; i < len; i++)
b[i] = a[i];
b = a;
}
free(b);
}C++实现
template<typename T>
void merge_sort(T arr[], int len) {
T *a = arr;
T *b = new T[len];
for (int seg = 1; seg < len; seg += seg) {
for (int start = 0; start < len; start += seg + seg) {
int low = start, mid = min(start + seg, len), high = min(start + seg + seg, len);
int k = low;
int start1 = low, end1 = mid;
int start2 = mid, end2 = high;
while (start1 < end1 && start2 < end2)
b[k++] = a[start1] < a[start2] ? a[start1++] : a[start2++];
while (start1 < end1)
b[k++] = a[start1++];
while (start2 < end2)
b[k++] = a[start2++];
}
T *temp = a;
a = b;
b = temp;
}
if (a != arr) {
for (int i = 0; i < len; i++)
b[i] = a[i];
b = a;
}
delete[] b;
}C++(递归版)
void Merge(vector<int> &Array, int front, int mid, int end) {
// preconditions:
// Array[front...mid] is sorted
// Array[mid+1 ... end] is sorted
// Copy Array[front ... mid] to LeftSubArray
// Copy Array[mid+1 ... end] to RightSubArray
vector<int> LeftSubArray(Array.begin() + front, Array.begin() + mid + 1);
vector<int> RightSubArray(Array.begin() + mid + 1, Array.begin() + end + 1);
int idxLeft = 0, idxRight = 0;
LeftSubArray.insert(LeftSubArray.end(), numeric_limits<int>::max());
RightSubArray.insert(RightSubArray.end(), numeric_limits<int>::max());
// Pick min of LeftSubArray[idxLeft] and RightSubArray[idxRight], and put into Array[i]
for (int i = front; i <= end; i++) {
if (LeftSubArray[idxLeft] < RightSubArray[idxRight]) {
Array[i] = LeftSubArray[idxLeft];
idxLeft++;
} else {
Array[i] = RightSubArray[idxRight];
idxRight++;
}
}
}
void MergeSort(vector<int> &Array, int front, int end) {
if (front >= end)
return;
int mid = (front + end) / 2;
MergeSort(Array, front, mid);
MergeSort(Array, mid + 1, end);
Merge(Array, front, mid, end);
}6.快速排序
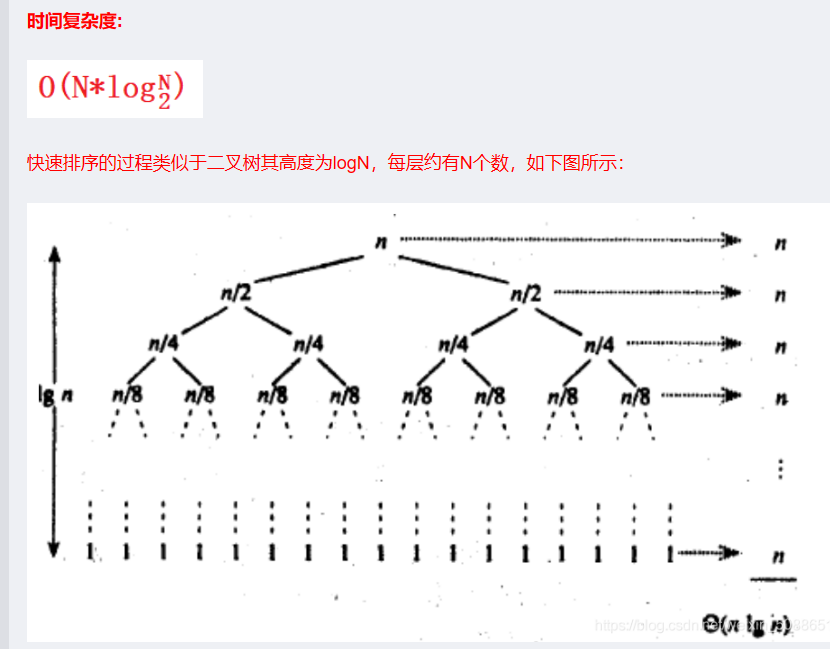
快速排序(Quick Sort)是一种常用的排序算法,也是一种分治算法。其基本思想是选择一个基准元素,将待排序序列分成两个子序列,使得一个子序列中所有元素都比基准元素小,另一个子序列中所有元素都比基准元素大,然后递归地对子序列进行排序。
具体实现过程如下:
选择一个基准元素,一般选择第一个元素或者随机选择一个元素。
将序列中所有比基准元素小的元素放在基准元素的左边,所有比基准元素大的元素放在右边。
对基准元素的左右两边重复上述过程,直到每个子序列只剩下一个元素。
C语言实现
typedef struct _Range {
int start, end;
} Range;
Range new_Range(int s, int e) {
Range r;
r.start = s;
r.end = e;
return r;
}
void swap(int *x, int *y) {
int t = *x;
*x = *y;
*y = t;
}
void quick_sort(int arr[], const int len) {
if (len <= 0)
return;
Range r[len];
int p = 0;
r[p++] = new_Range(0, len - 1);
while (p) {
Range range = r[--p];
if (range.start >= range.end)
continue;
int mid = arr[(range.start + range.end) / 2];
int left = range.start, right = range.end;
do {
while (arr[left] < mid) ++left;
while (arr[right] > mid) --right;
if (left <= right) {
swap(&arr[left], &arr[right]);
left++;
right--;
}
} while (left <= right);
if (range.start < right) r[p++] = new_Range(range.start, right);
if (range.end > left) r[p++] = new_Range(left, range.end);
}
}C++实现
int Paritition1(int A[], int low, int high) {
int pivot = A[low];
while (low < high) {
while (low < high && A[high] >= pivot) {
--high;
}
A[low] = A[high];
while (low < high && A[low] <= pivot) {
++low;
}
A[high] = A[low];
}
A[low] = pivot;
return low;
}
void QuickSort(int A[], int low, int high) //快排母函数
{
if (low < high) {
int pivot = Paritition1(A, low, high);
QuickSort(A, low, pivot - 1);
QuickSort(A, pivot + 1, high);
}
}
7.堆排序
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。分为两种方法:
大顶堆:每个节点的值都大于或等于其子节点的值,在堆排序算法中用于升序排列;
小顶堆:每个节点的值都小于或等于其子节点的值,在堆排序算法中用于降序排列;
算法步骤
1创建一个堆 H[0……n-1];
2把堆首(最大值)和堆尾互换;
3把堆的尺寸缩小 1,并调用 shift_down(0),目的是把新的数组顶端数据调整到相应位置;
4重复步骤 2,直到堆的尺寸为 1。
C语言代码实现
#include <stdio.h>
#include <stdlib.h>
void swap(int *a, int *b) {
int temp = *b;
*b = *a;
*a = temp;
}
void max_heapify(int arr[], int start, int end) {
// 建立父節點指標和子節點指標
int dad = start;
int son = dad * 2 + 1;
while (son <= end) { // 若子節點指標在範圍內才做比較
if (son + 1 <= end && arr[son] < arr[son + 1]) // 先比較兩個子節點大小,選擇最大的
son++;
if (arr[dad] > arr[son]) //如果父節點大於子節點代表調整完畢,直接跳出函數
return;
else { // 否則交換父子內容再繼續子節點和孫節點比較
swap(&arr[dad], &arr[son]);
dad = son;
son = dad * 2 + 1;
}
}
}
void heap_sort(int arr[], int len) {
int i;
// 初始化,i從最後一個父節點開始調整
for (i = len / 2 - 1; i >= 0; i--)
max_heapify(arr, i, len - 1);
// 先將第一個元素和已排好元素前一位做交換,再重新調整,直到排序完畢
for (i = len - 1; i > 0; i--) {
swap(&arr[0], &arr[i]);
max_heapify(arr, 0, i - 1);
}
}
int main() {
int arr[] = { 3, 5, 3, 0, 8, 6, 1, 5, 8, 6, 2, 4, 9, 4, 7, 0, 1, 8, 9, 7, 3, 1, 2, 5, 9, 7, 4, 0, 2, 6 };
int len = (int) sizeof(arr) / sizeof(*arr);
heap_sort(arr, len);
int i;
for (i = 0; i < len; i++)
printf("%d ", arr[i]);
printf("\n");
return 0;
}C++实现
#include <iostream>
#include <algorithm>
using namespace std;
void max_heapify(int arr[], int start, int end) {
//建立父节点和字节点
int dad = start;
int son = dad * 2 + 1;
while (son <= end) {
if (son + 1 <= end && arr[son] < arr[son + 1]) // 比较两个子节点大小,选择大的
son++;
if (arr[dad] > arr[son]) // 如果父节点大于子节点代表完整,退出函数
return;
else {
swap(arr[dad], arr[son]);
dad = son;
son = dad * 2 + 1;
}
}
}
void heap_sort(int arr[], int len) {
for (int i = len / 2 - 1; i >= 0; i--)
max_heapify(arr, i, len - 1);
for (int i = len - 1; i > 0; i--) {
swap(arr[0], arr[i]);
max_heapify(arr, 0, i - 1);
}
}
int main() {
int arr[] = { 3, 5, 3, 0, 8, 6, 1, 5, 8, 6, 2, 4, 9, 4, 7, 0, 1, 8, 9, 7, 3, 1, 2, 5, 9, 7, 4, 0, 2, 6 };
int len = (int) sizeof(arr) / sizeof(*arr);
heap_sort(arr, len);
for (int i = 0; i < len; i++)
cout << arr[i] << ' ';
cout << endl;
return 0;
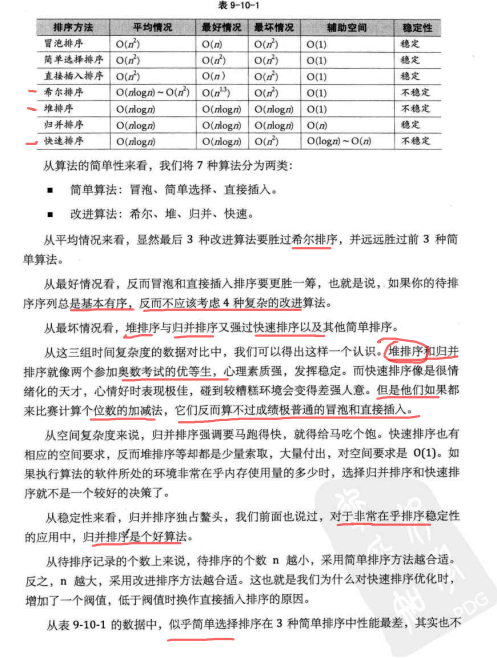
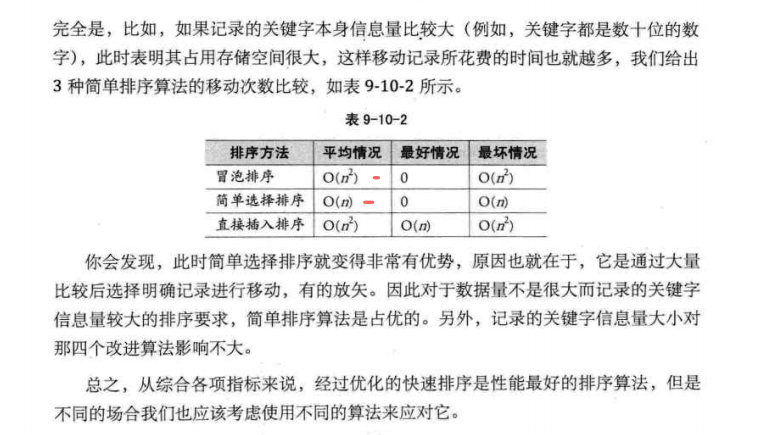
}稳定性以及复杂度
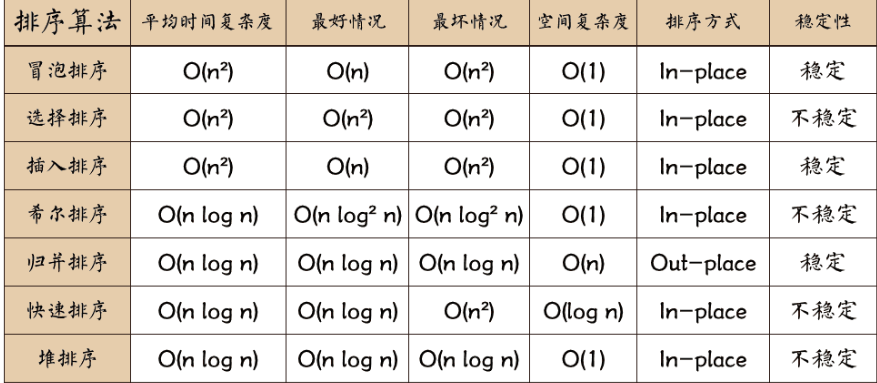
大话数据结构关于排序算法的的总结: