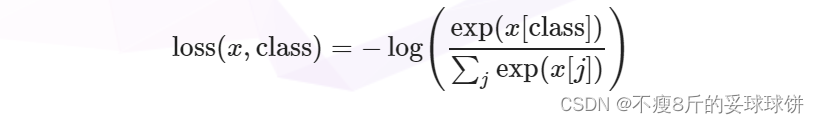Python解题 - CSDN周赛第30期

Python解题 - CSDN周赛第30期 - 天然气订单

news2024/12/23 5:39:25

本期比赛的在线测试系统好像出了点问题，导致很多选手最后提交的分数是0，而问哥也遇到好几次提交后一直显示“运行中”而没有结果的情况。鉴于之前遇到过类似情况，不停地刷新页面才得以继续。但是此问题已经存在并持续了好几期，极大地影响了参赛体验，希望官方重视起来并尽快修复。

第一题：天然气订单

天然气运输成本昂贵，危险性高，为了节省运输成本，提倡绿色环保，需要尽可能的优化订单配送，比如相同地区的天然气订单可以一次性配送。现需要向多个地区运输天然气。但是同一个地区可能有多个订单需求。当前仅只知道某些成对的订单是同一个地区的，同一个地区的天然气需要尽可能一次性配送从而降低运输成本，所以需要尽可能的将同一个地区的订单放在一起。订单的编号是1到n。

输入描述：输入第一行是两个正整数n，m，表示订单的数量和已知的关系数量。(1<=n，m<=10000)；接下来有m行，每行两个正整数a和b，表示a号订单和b号订单属于同一个地区(1<=a,b<=n)；接下来有n行，每行两个正整数x，y，分别表示该车完成A地任务的利润和B地任务的利润。

输出描述：输出第一行包含一个整数x，表示这些订单共来自x个不同的地区。接下来的输出包含x行，每行表示输出若干个订单编号，表示这些订单属于同一个地区，按照订单编号升序输出。优先输出最小的订单编号较小的地区。

示例：

示例
输入 7 6
1 2
2 2
3 2
4 5
5 4
6 7
输出 3
1 2 3
4 5
6 7

分析

看到“xx的编号是1到n”的描述，首先想到的就是并查集的数据结构。然后发现此题还是求连通子图（同属一个地区的订单），类似此前考过的《蚂蚁家族》和《交际圈》。但是本题除了要求连通子图的个数，还要输出每个子图中的所有节点。

使用深搜（dfs）应该也能做，如果用并查集的话，还需要用到并查集的两个优化操作：路径压缩和按秩合并，不然可能会超时。又因为最后要输出每个连通子图的所有节点，只需要把按秩合并后的并查集中最早出现的“祖先”作为键，其他成员作为值，生成一个字典即可。最后字典中键的个数即连通子图的个数，而每个连通子图的节点也已经排好序了，直接输出即可。

参考代码

n, m = map(int, input().strip().split())
nodes = list(range(n+1))

# 路径压缩的查集操作
def find(n):
    if nodes[n] == n: return n
    nodes[n] = find(nodes[n])
    return nodes[n]

for _ in range(m):
    a, b = map(int, input().strip().split())
    aa = find(a)
    bb = find(b)
    # 按秩合并的并集操作
    if aa < bb: nodes[bb] = aa
    else: nodes[aa] = bb

res = dict()
for i in range(1, n+1):
    if nodes[i] == i:
        res[i] = [i]
    else:
        res[find(nodes[i])].append(i)

print(len(res))
for value in res.values():
    print(*value)

并查集的操作很简单，简单来讲，路径压缩就是每次查找时都把查找路径中所有的节点指向目前的“公共祖先”，使得后面的查找不用再重复查找路径；而按秩合并就是优先把数字更小（排在前面）的节点作为“祖先” ，这样可以使得并查集的树形结构深度最小，更加平衡。而本解法实际利用了按秩排序的最早公共祖先以及排序性质。

第二题：小艺读书

书是人类进步的阶梯。小艺每周因为工作的原因会选择性的每天多读几页或者少读几页。小艺想知道一本n页的书她会在周几读完。

输入描述：第一行输入n(1<=n<=1000)；第二行输入7个整数，分别表示周一~周日的读书页数p(0<=p<=1000)。（不考虑7个整数都为0的情况）

输出描述：输出答案。（1-7）

示例：

示例
输入 100
15 20 20 15 10 30 45
输出
6

分析

题目描述不是特别好，没有说明从哪一天开始读书，那就只能默认从周一开始了，虽然常识里感觉怪怪的。而测试用例也不全面，没有周日读完的情况，也就是输出7。对于考察循环数组的简单题来说，不完整的测试用例使得本题更水了。

解题方法就是循环模拟，下标每次加一，如果循环至下一周，下标要对7取模。最后输出下标即可。要注意的是如果是周日读完，此时下标为0，要特判输出7，但是本题的测试用例没有出现这种情况。

参考代码

n = int(input().strip())
pages = [int(item) for item in input().strip().split()]
i = 0
while n > 0:
    n -= pages[i]
    i = (i+1)%7
if i == 0: print(7)
else: print(i)

第三题：买苹果

小易去附近的商店买苹果，奸诈的商贩使用了捆绑交易，只提供6个每袋和8个每袋的包装(包装不可拆分)。可是小易现在只想购买恰好n个苹果，小易想购买尽量少的袋数方便携带。如果不能购买恰好n个苹果，小易将不会购买。

输入描述：输入一个整数n，表示小易想购买n(1 ≤ n ≤ 100)个苹果

输出描述：输出一个整数表示最少需要购买的袋数，如果不能买恰好n个苹果则输出-1

示例：

示例
输入 20
输出
3

分析

我猜本题原本是想考察完全背包，但是由于数据范围很小， $1\leq n\leq 100$ ，使用暴力穷举也能过。

因为要买恰好 $n$ 个苹果，所以最多只能买 $\frac{n}{6}$ 袋每袋6个装的苹果，和 $\frac{n}{8}$ 袋每袋8个装的苹果，均向下取整（有点像百钱百鸡）。于是设 $0\leq i\leq \frac{n}{6}$ ， $0\leq j\leq \frac{n}{8}$ ，暴力枚举每一种 $(i,j)$ 的组合，如果 $6*j+8*j=n$ ，就把 $i+j$ 的结果保存在集合里。最后输出集合中的最小值即可。如果不存在满足该等式的 $(i,j)$ ，则集合为空，输出 -1。

参考代码

n = int(input().strip())
res = set()
for i in range((n//6)+1):
    for j in range((n//8)+1):
        if 6*i + 8*j == n:
            res.add(i+j)
if res: print(min(res))
else: print(-1)

算法复杂度为 $O(n^2)$ ，准确来讲计算了 $\frac{n^2}{48}$ 次，所以当 n 很小时，和使用DP完全背包的算法复杂度 $O(mn)$ （m为物品的种类，本题为2）没有什么区别。关于完全背包，感兴趣的同学可以参考网上资料，问哥之前的文章也有涉及，此处不再赘述。

第四题：圆桌

有N个客人与足够多张的圆桌。主人安排每位客人坐在一个圆桌边，但是每位客人希望自己左右边上分别有一些空座位，不然会觉得害羞。注意，如果一个客人所在的圆桌只有他一个人，那么他左边的空座位数量就是他右边的空座位数量。试问主人需要准备多少个座位，才能让每个客人舒适的坐下。

输入描述：第一行输入一个整数N，(1<=N<=10000),代表客人的数量；接下来N行，每行两个整数li与ri，(1<=i<=N,1<=li<=ri<=1000000000)，代表第i位客人希望左边有li个空座位，右边有ri个空座位。

输出描述：输出一个整数，代表主人需要准备的最少座位数量。

示例：

示例
输入 3
1 1
1 1
1 1
输出 6