蓝桥杯训练day1

news2024/12/23 5:16:21

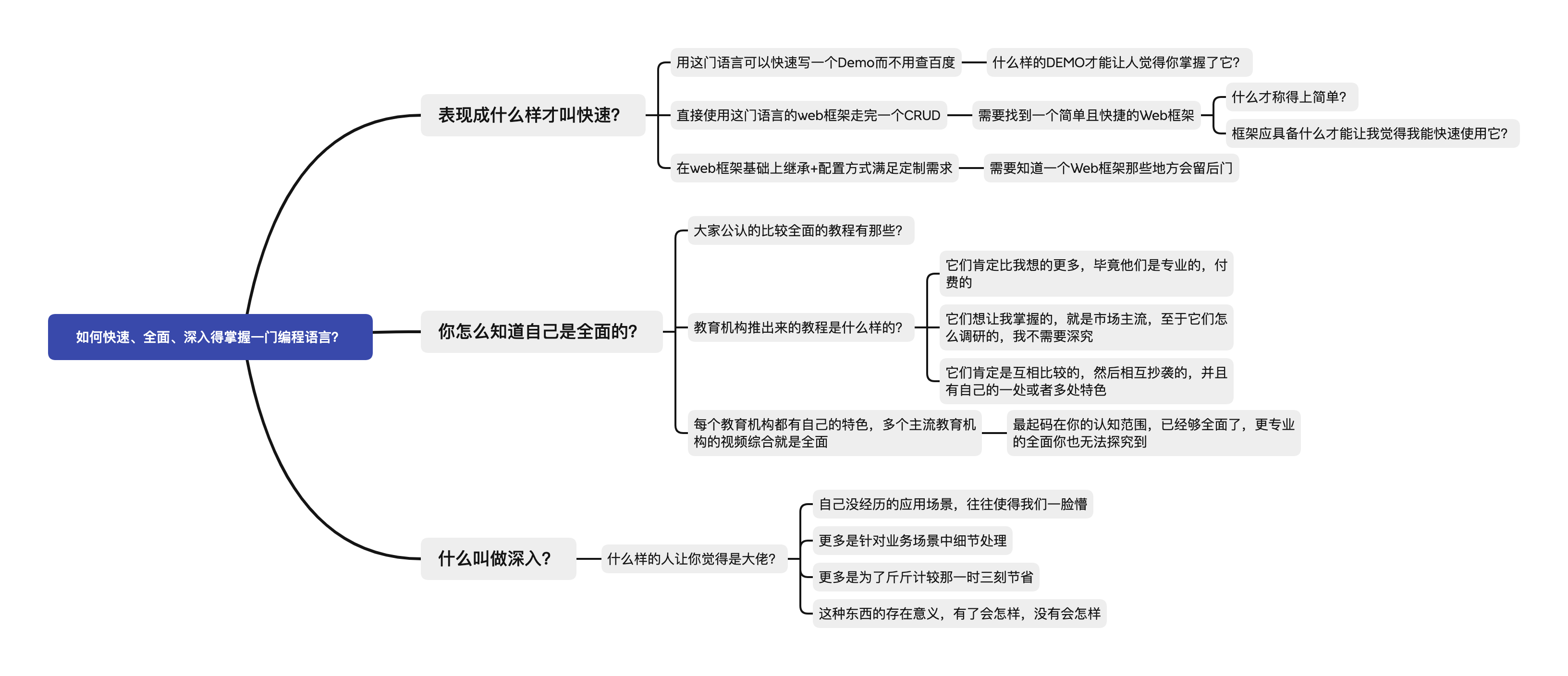
前缀和+差分

  • 1.前缀和
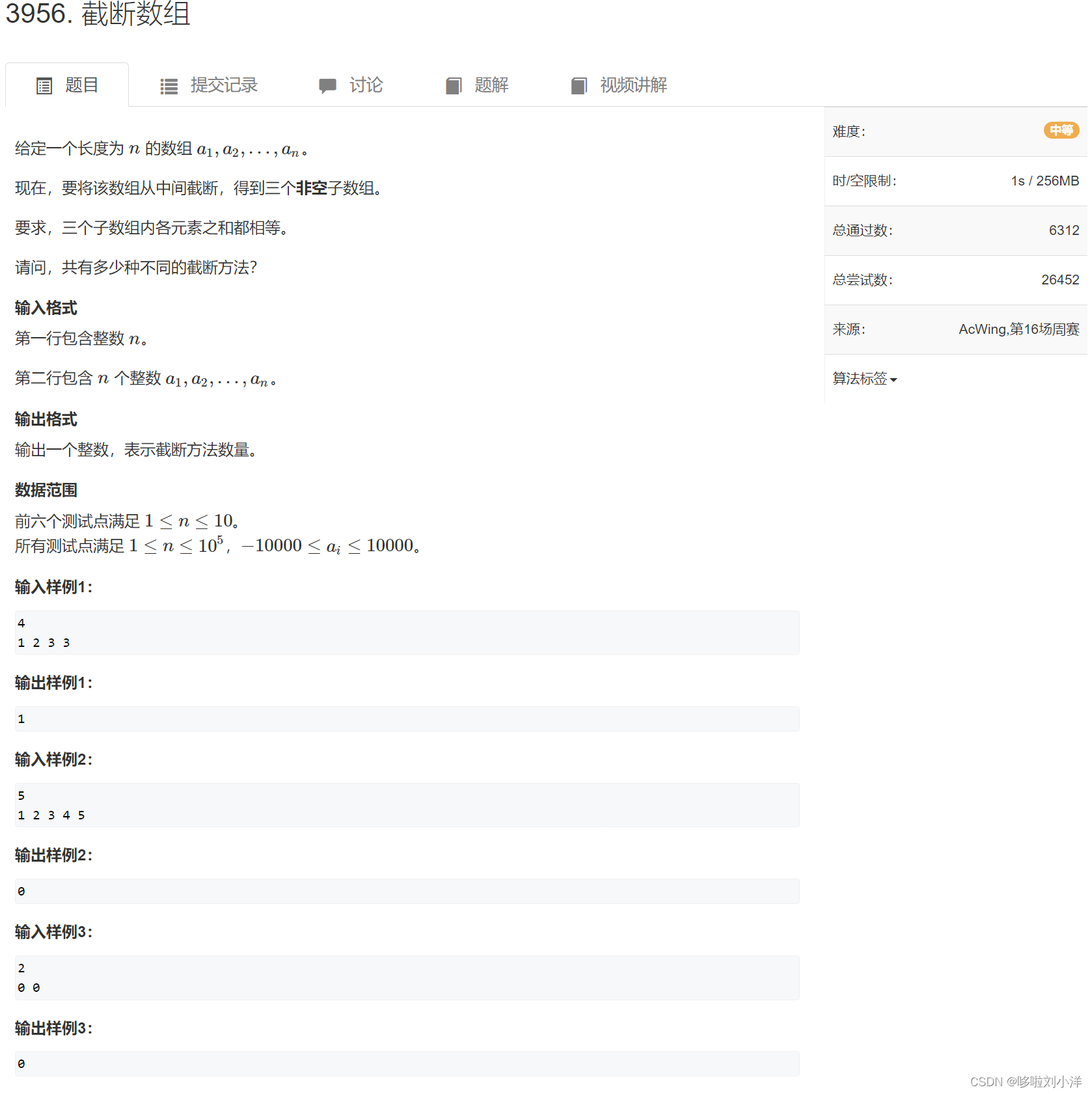
    • (1)3956. 截断数组
    • (2)795. 前缀和
    • (3)796. 子矩阵的和
    • (4)1230. K倍区间
    • (5)99. 激光炸弹
  • 2.差分
    • (1)797. 差分
    • (2)差分矩阵
    • (3)3729. 改变数组元素
    • (4)100. 增减序列

1.前缀和

(1)3956. 截断数组

在这里插入图片描述

方法1：暴力
先用两个数组分别保存前缀和，后缀和。然后使用贪心思想来枚举后缀和的下标。
只有后缀和满足1/3的下标大于前缀和的下标，就加（具体看代码）过（19/22）数据

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1e5 + 10;

int n;
int a[N];
int pre[N];
int npre[N];
int h1[N], h2[N];
int cnt1, cnt2;
int sum = 0;
int main()
{
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i];
        sum += a[i];
    }

    int part = sum / 3;
    pre[0] = 0;  //pre[i]表示前i个数的总和，这里下标从1开始有意义
    for (int i = 1; i <= n; i++)    //前缀和
    {
        pre[i] = pre[i - 1] + a[i];
        if (pre[i] == part)h1[++cnt1] = i;
    }

    npre[n] = a[n];
    if (npre[n] == part)h2[++cnt2] = n;
    for (int i = n - 1; i >= 1; i--)   //后缀和
    {
        npre[i] = npre[i + 1] + a[i];
        if (npre[i] == part)h2[++cnt2] = i;
    }
    //如此一来，存储了第一部分的part值的下标（从小到大）
    //又存储了第二部分的part值的下标（从大到小）

    //固定第二部分的下标，然后找第一部分的下标（由于从小到大，如果第二部分的下标大于第一部分下标的,则第一部分剩下的下标个数等于
    //当前答案个数。
    //然后枚举第二部分的下标，反复即可

    int ans = 0;   //记录答案

    while (cnt2)
    {
        int r = h2[cnt2];
        int temp = cnt1;   //第一部分的下标
        while (temp)
        {
            if (r > h1[temp]+1)  //可以分成三个部分
            {
                ans = ans + temp;
                break;
            }
            temp--;
        }
        cnt2--;
    }

    cout << ans << endl;
    return 0;

}

方法2：动态规划
枚举第二部分的位置，然后找第一部分有多少分割方案。使用动态规划的技巧来减少计算

#include<iostream>
#include<cstring>
using namespace std;
const int N=100010;


int n;
int cnt;
long long int ans=0;

int pre[N];

int main()
{
    cin>>n;
    int x;
    for(int i=1;i<=n;i++)
    {
        cin>>x;
        pre[i]=pre[i-1]+x;
    }
    if(pre[n]%3)
    {
        cout<<"0";
        return 0;
    }
    else
    {
        for(int i=2;i<=n-1;i++)
        {
            if(pre[i-1]==pre[n]/3)cnt++;
            if(pre[i]==pre[n]/3*2)ans+=cnt;
        }
    }
    cout<<ans;
    return 0;
}

(2)795. 前缀和

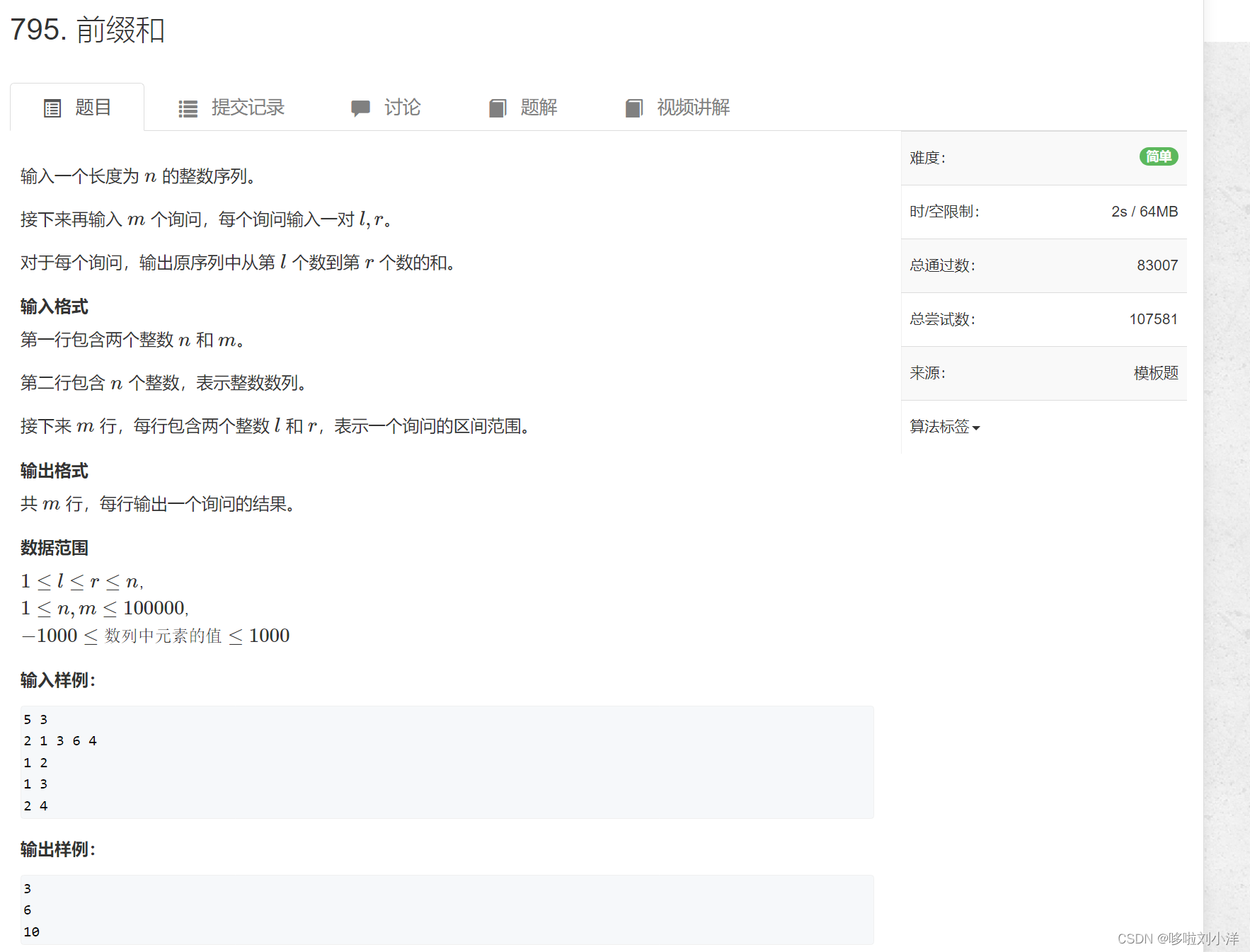
在这里插入图片描述

前缀和最简单的题目，模板题
用一个数组来记录前i个元素的和.

#include<iostream>
#include<cstring>
using namespace std;

const int N=100010;

int n,m;
int a[N];
int pre[N];

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)  //下标从1开始
    {
        cin>>a[i];
        pre[i]=pre[i-1]+a[i];
    }
        

    while(m--)
    {
        int l,r;
        cin>>l>>r;
        cout<<pre[r]-pre[l-1]<<endl;    //注意是pre[l-1],要包括a[l]那个数
    }
    return 0;
}

(3)796. 子矩阵的和

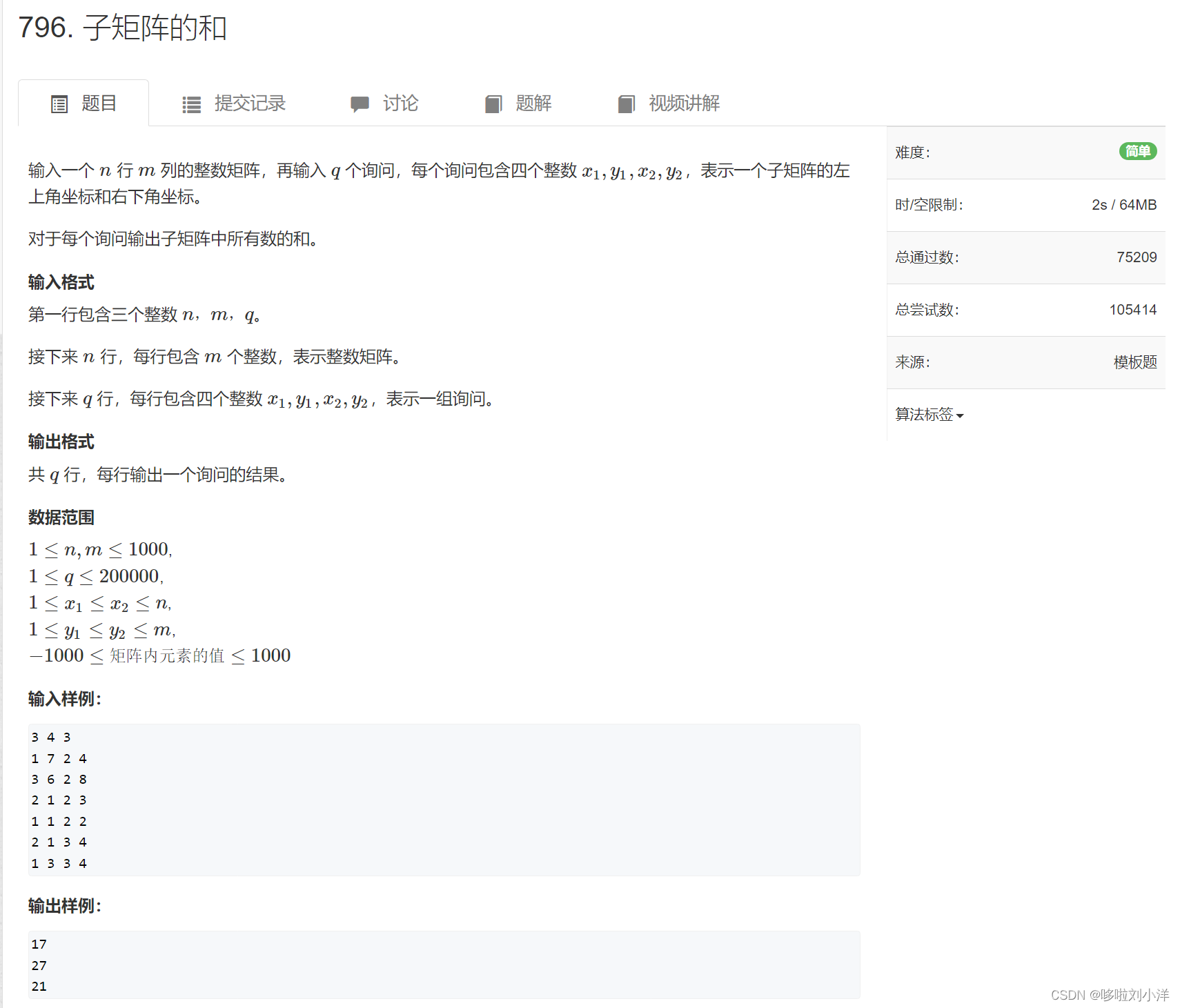
在这里插入图片描述

二维前缀和,
模拟过程，然后优化，反复几次即可掌握

#include<iostream>
using namespace std;

const int N=1010;

int g[N][N];  //矩阵
int pre[N][N];  //左上角为（1，1），右下角是（i，j)的矩阵的和

int n,m,q;


int main()
{
    cin>>n>>m>>q;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
        {
            cin>>g[i][j];
            pre[i][j]=pre[i][j-1]+pre[i-1][j]-pre[i-1][j-1]+g[i][j];
        }

    while(q--)
    {
        int x1,x2,y1,y2;
        cin>>x1>>y1>>x2>>y2;
        cout<<pre[x2][y2]-pre[x1-1][y2]-pre[x2][y1-1]+pre[x1-1][y1-1]<<endl;
    }
    return 0;
}

(4)1230. K倍区间

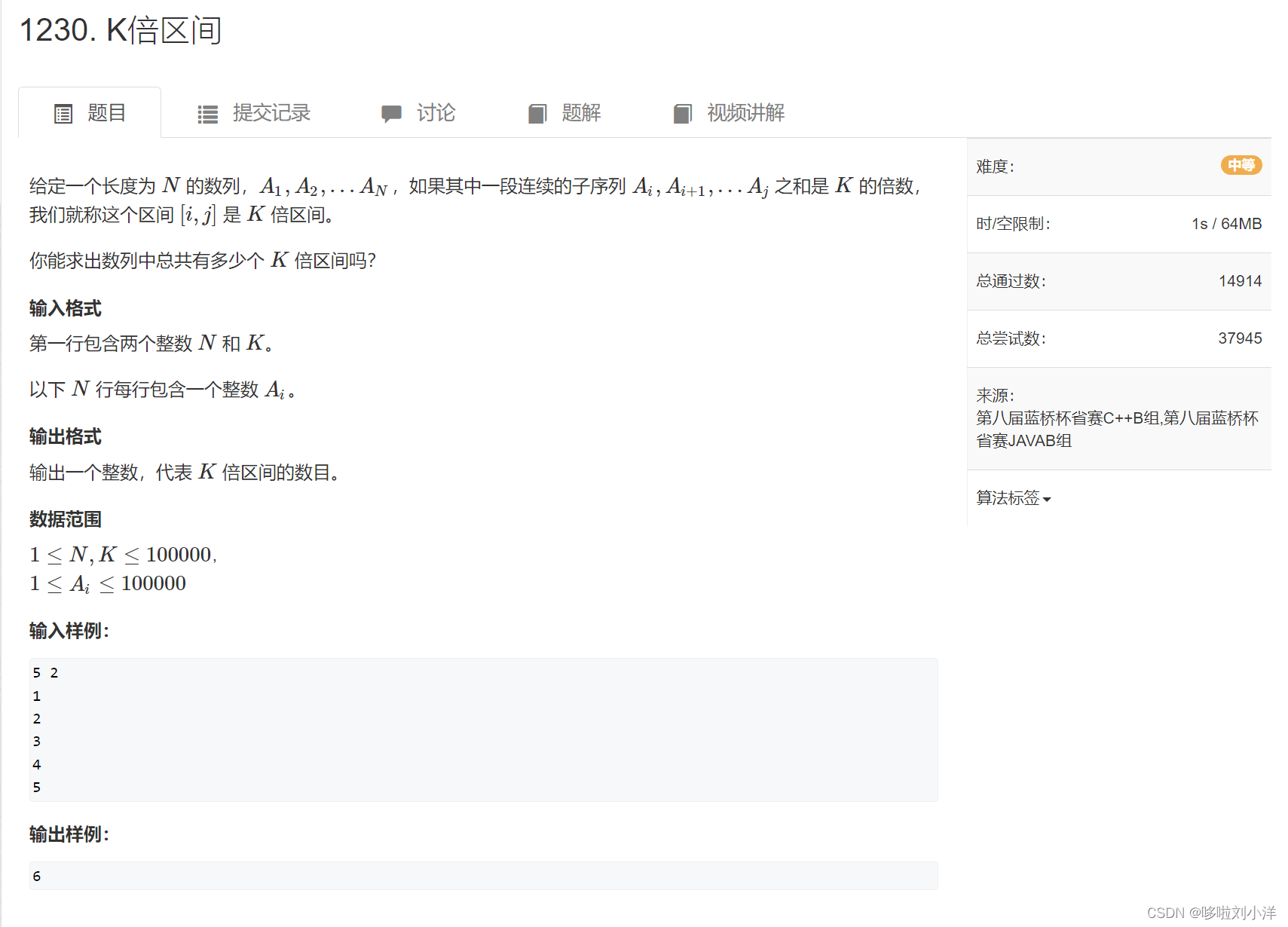
在这里插入图片描述

这个题目，看的第一感觉应该是个简单题，没想到是个中等题，暴力只能过一半数据。
暴力：

#include<iostream>
#include<cstring>
using namespace std;

const int N=1e5+10;

int n,k;

int a[N];
int pre[N];
int ans=0;

int main()
{
    cin>>n>>k;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        a[i]%=k;
        pre[i]=pre[i-1]+a[i];
    }
    
    for(int i=1;i<=n;i++)
    {
        int temp=0;
        for(int j=i;j<=n;j++)
        {
            temp+=a[j];
            if(temp%k==0)ans++;
        }
    }
    cout<<ans;
    return 0;
}

想到
pre[r]-pre[l-1]=k
pre[r[=pre[l-1]+k
用pre[r]作为key，r作为key存储到哈希表，没想到也只多过一个数据

#include<iostream>
#include<cstring>
#include<unordered_map>
#include<vector>
using namespace std;

const int N=1e5+10;

int n,k;

int a[N];
int pre[N];
int ans=0;

int main()
{
    cin>>n>>k;
    unordered_map<int,vector<int>>Hash;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        pre[i]=(pre[i-1]+a[i])%k;
        Hash[pre[i]].push_back(i);
    }
    
    //利用前缀和
    
    for(int i=1;i<=n;i++)
    {
        if(Hash.count((pre[i-1]+k)%k)!=0) //找到区间
        {
            vector<int>t=Hash[(pre[i-1]+k)%k];
            for(int j=0;j<t.size();j++)
            {
                if(i<=t[j])
                {
                    ans+=t.size()-j;
                    break;
                }
            }
        }
    }
    
    cout<<ans;
    return 0;
}

看了题解，发现距离答案一步之遥。在于
pre[r]-pre[l-1]=k等价于 pre[r]%k=pre[l-1]%k
所以找到两个前缀和相同的就好了，再利用一点动态规划的技巧.

#include<iostream>
using namespace std;
const int N=100010;

int a[N];
int pre[N];
int Hash[N];

int n,k;


int main()
{
    cin>>n>>k;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        pre[i]=(pre[i-1]+a[i])%k;
    }
    long long ans=0;
    Hash[0]=1;  //由于对k取余，所以第一个元素可能就是k
    for(int i=1;i<=n;i++)   //从前往后遍历，到当前遍历到的点，前面有多少和他一样的值
    {
        ans+=Hash[pre[i]];
        Hash[pre[i]]++;
    }
    cout<<ans;
    return 0;
    
}

(5)99. 激光炸弹

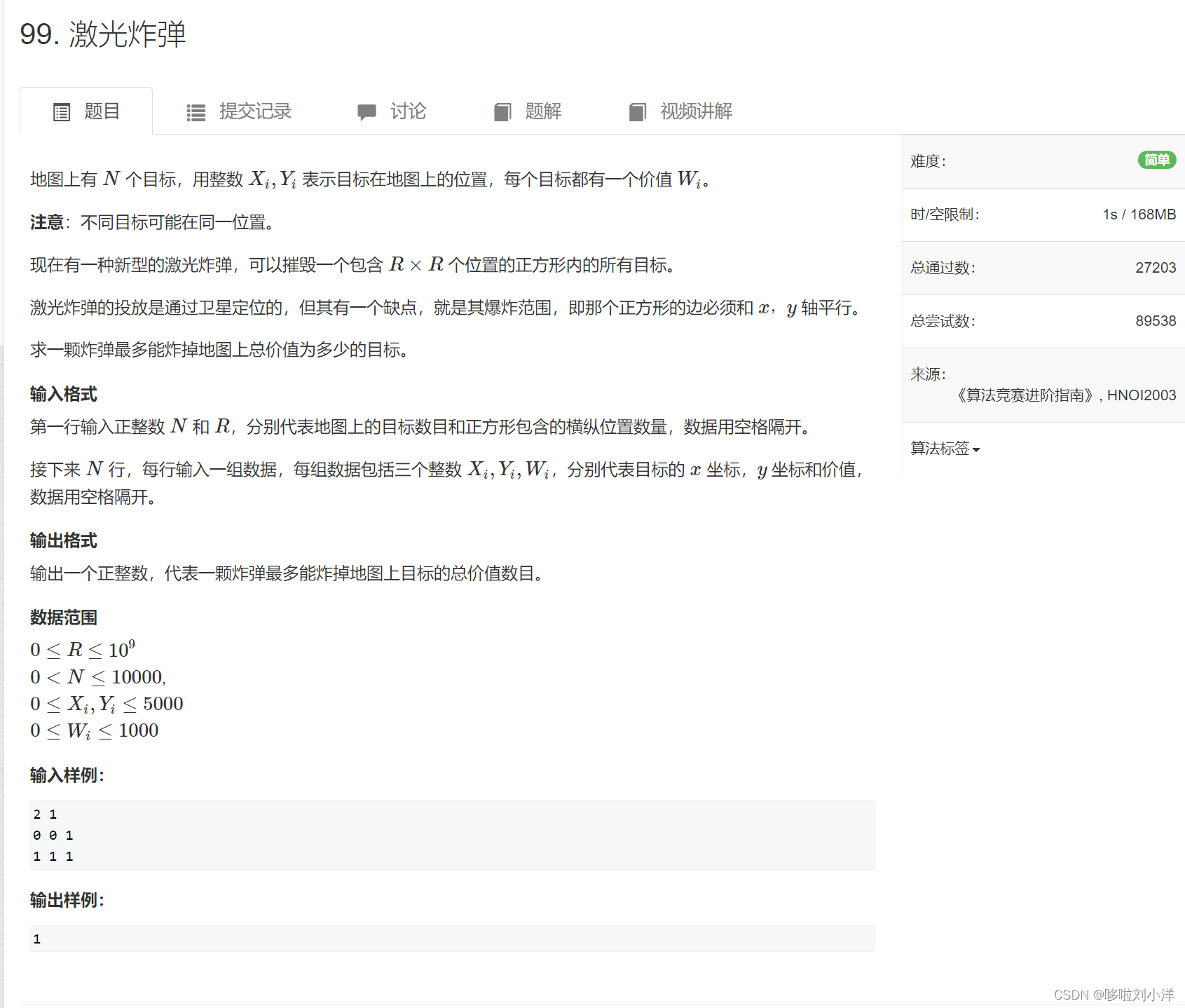
在这里插入图片描述
暴力

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

const int N=5010;

int n,r;
int pre[N][N];

int main()
{
    cin>>n>>r;   //n表示目标点个数，r表示炸弹的范围
    r = min(r, 5001);
    while(n--)
    {
        int x,y,v;
        cin>>x>>y>>v;
        pre[x+1][y+1]+=v;
    }
     
    //前缀和
    for(int i=1;i<=5001;i++)
        for(int j=1;j<=5001;j++)
            pre[i][j]=pre[i-1][j]+pre[i][j-1]-pre[i-1][j-1]+pre[i][j];
    
    int ans=0;
    //枚举右下角
    for(int i=r;i<=5001;i++)
    {
        for(int j=r;j<=5001;j++)
            ans=max(ans,pre[i][j]-pre[i-r][j]-pre[i][j-r]+pre[i-r][j-r]);
    }
    cout<<ans;
    return 0;
}

2.差分

(1)797. 差分

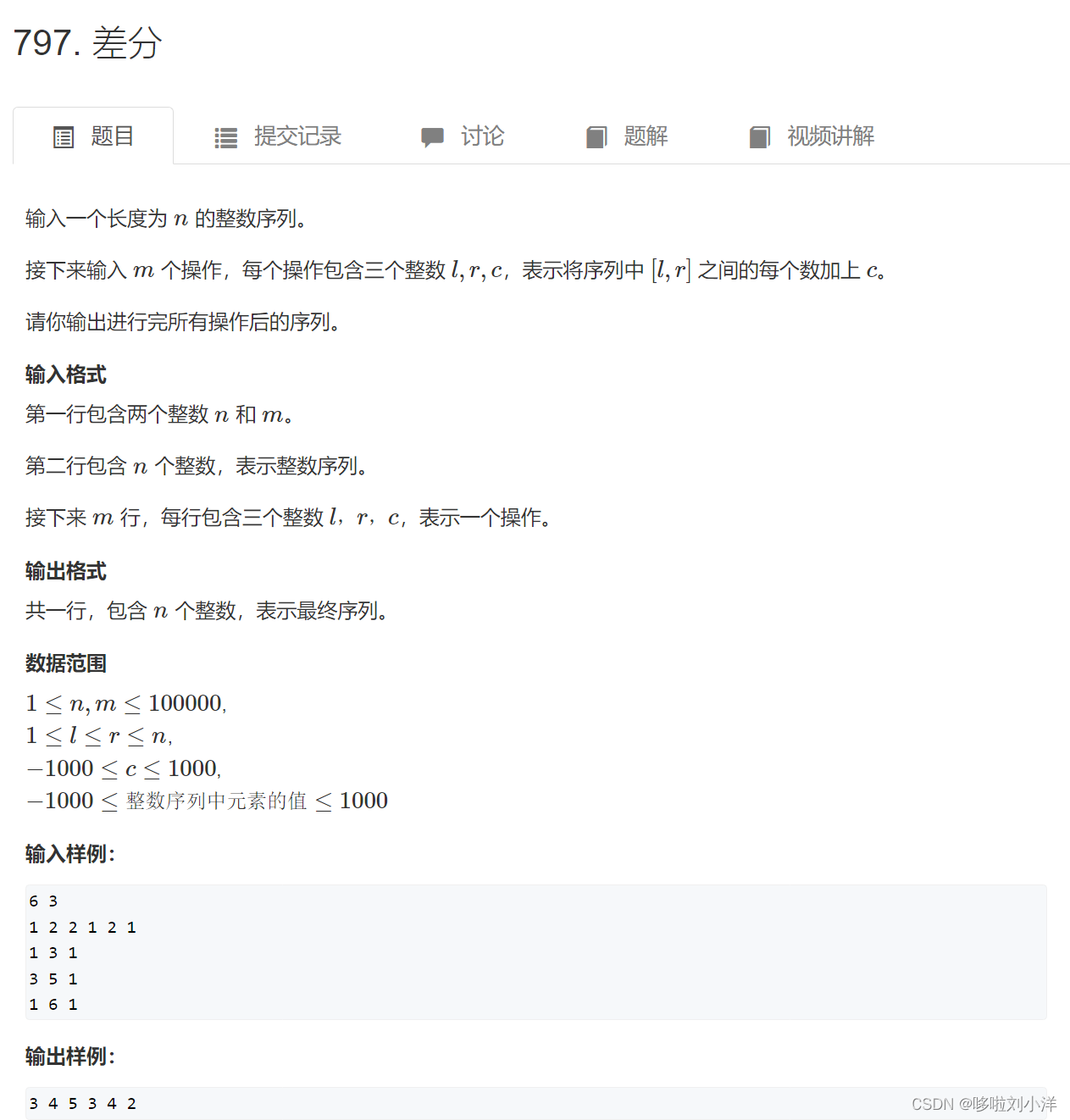
在这里插入图片描述
什么是差分。
一句话：就是前缀和运输的逆运算.

#include<iostream>
#include<algorithm>
using namespace std;


const int N=1e5+10;
int a[N];
int b[N];

int n;
int T;

int main()
{
    cin>>n>>T;
    for(int i=1;i<=n;i++)  //相当于，b是原数组，a是b的前缀和
    {
        cin>>a[i];
        b[i]=a[i]-a[i-1];
    }
        
    while(T--)
    {
        int l,r,c;
        cin>>l>>r>>c;
        b[l]+=c;
        b[r+1]-=c;
    }
    int sum=0;
    for(int i=1;i<=n;i++)
    {
        sum+=b[i];
        cout<<sum<<" ";
    }
    return 0;
}

(2)差分矩阵

在这里插入图片描述

同二维前缀和一样，就是扩展一个维度(但是很难哦）

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;


const int N=1010;

int pre[N][N];
int a[N][N];


int n,m,q;

int  main()
{
    cin>>n>>m>>q;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
        {
            cin>>pre[i][j];
            a[i][j]=pre[i][j]-pre[i-1][j]-pre[i][j-1]+pre[i-1][j-1];
        }
    while(q--)
    {
        int x1,x2,y1,y2,c;
        cin>>x1>>y1>>x2>>y2>>c;
        a[x1][y1]+=c;
        a[x1][y2+1]-=c;
        a[x2+1][y1]-=c;
        a[x2+1][y2+1]+=c;
    }
    int sum=0;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
        {
            pre[i][j]=pre[i-1][j]+pre[i][j-1]-pre[i-1][j-1]+a[i][j];
            cout<<pre[i][j]<<" ";
            if(j==m)cout<<endl;
        }
    return 0;
}

(3)3729. 改变数组元素

在这里插入图片描述

说实话，这个题目放在差分下面，完全不知道和差分有什么关系。
就从后往前读一遍看看哪些位置可以为1就可以了，应该是个简单到不能再简单的题，，，

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;

const int N=2*(1e5+10);
int a[N];  //操作数组
int b[N];   //答案数组
int T,n;

//假设两个数组a，b，a是原数组，b是a的前缀和数组。
//那么a是b的差分，b是a的原数组

int main()
{
    cin>>T;
    while(T--)
    {
        memset(b,0,sizeof b);
        cin>>n;
        for(int i=1;i<=n;i++)
            cin>>a[i];
        int cnt=a[n];
        for(int i=n;i>=1;i--)
        {
            cnt=max(cnt,a[i]);
            if(cnt>=1)
            {
                b[i]=1;
                cnt--;
            }
        }
        for(int i=1;i<=n;i++)
            cout<<b[i]<<" ";
        cout<<endl;
    }
    return 0;
}

(4)100. 增减序列

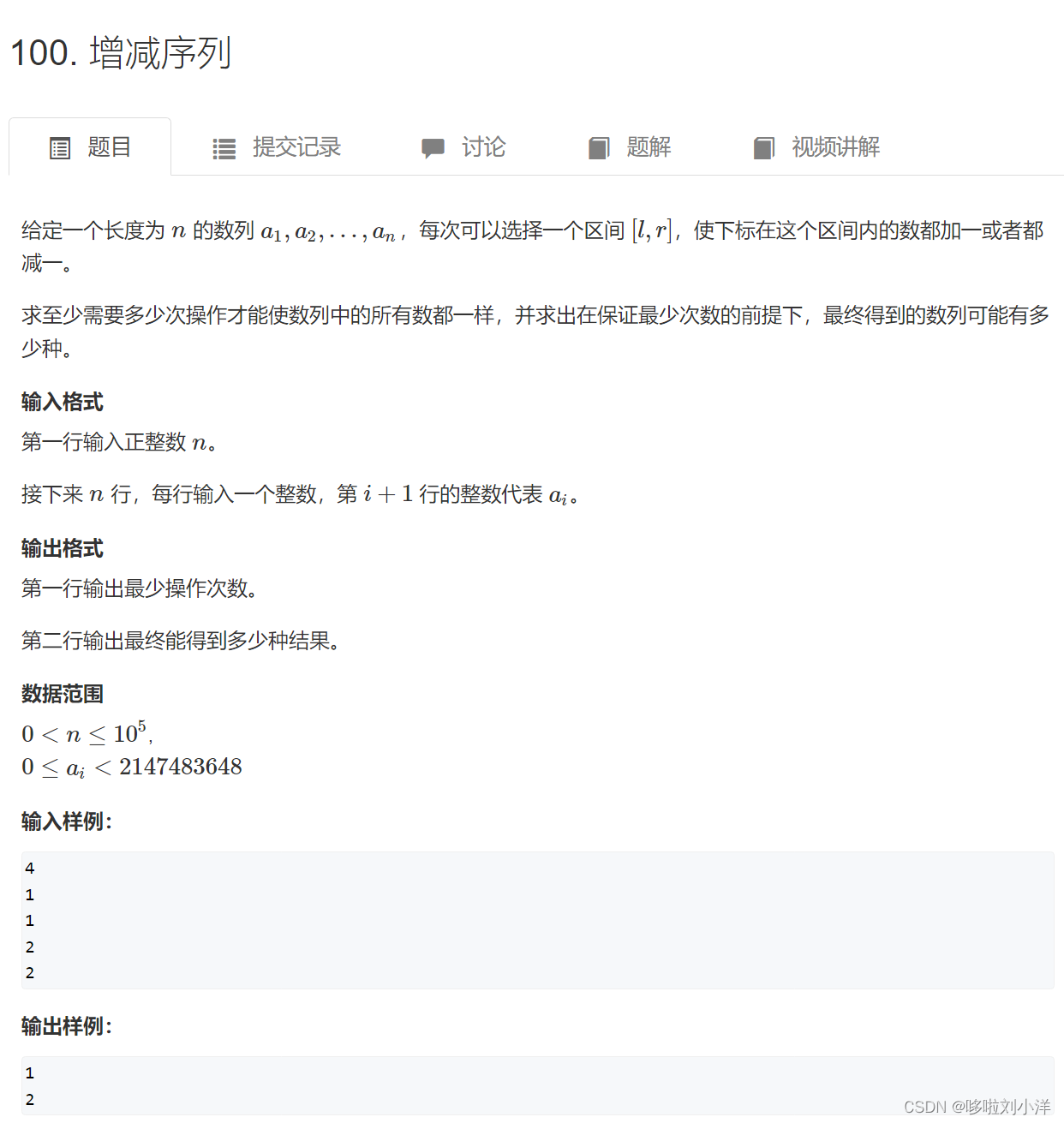
在这里插入图片描述
这个题目难啊，由于所有的数都要一样，所有差分数组必须除了第一个数其余全是0.由于差分数组每次操作都需要b[L]+1,b[R+1]-1或b[L]-1,b[R+1]+1.所以将正数和负数相互抵消后，剩下的数要么和b[1]抵消，要么和b[n+1]抵消。

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

const int N=1e5+10;

long long int a[N];
long long int b[N];

int n;

int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        b[i]=a[i]-a[i-1];
    }
    
    long long int c1=0,c2=0;  //c1记录正数和，c2记录负数和
    for(int i=2;i<=n;i++)
    {
        if(b[i]>=0)c1+=b[i];
        else    c2+=b[i];
    }
    long long int ans=min(abs(c1),abs(c2))+abs(abs(c1)-abs(c2));  //操作个数
    long long int count=abs(abs(c1)-abs(c2))+1;
    cout<<ans<<endl<<count<<endl;
    
    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/359100.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

如何快速、全面、深入地掌握一门编程语言

如何快速、全面、深入地掌握一门编程语言

思考路线 如何快速&#xff1f; 什么样的Demo才能让人觉得你掌握了它&#xff1f; 空 判断&#xff1a;构造一个可以判断所有空的 is_empty 函数 for 循环&#xff1a;i 和 集合迭代两种 时间获取&#xff1a;年/月/日 时分秒 时间戳与时间格式互转 休眠时间函数 字符串处理…
阅读更多...
对比学习MoCo损失函数infoNCE理解（附代码）

对比学习MoCo损失函数infoNCE理解（附代码）

MoCo loss计算采用的损失函数是InfoNCE&#xff1a; ​​ 下面是MoCo的伪代码&#xff0c;MoCo这个loss的实现就是基于cross entropy loss。 将k作为q的正样本&#xff0c;因为k与q是来自同一张图像的不同视图&#xff1b;将queue作为q的负样本&#xff0c;因为queue中含有大量…
阅读更多...
【Python学习笔记】44.Python3 MongoDB和urllib

【Python学习笔记】44.Python3 MongoDB和urllib

前言 本章介绍Python的MongoDB和urllib。 Python MongoDB MongoDB 是目前最流行的 NoSQL 数据库之一&#xff0c;使用的数据类型 BSON&#xff08;类似 JSON&#xff09;。 PyMongo Python 要连接 MongoDB 需要 MongoDB 驱动&#xff0c;这里我们使用 PyMongo 驱动来连接。…
阅读更多...
Ansys Zemax / SPEOS | 光源文件转换器

Ansys Zemax / SPEOS | 光源文件转换器

本文解释了如何在 SPEOS 与 Zemax 之间转换二进制光源文件。 下载 联系工作人员获取附件 简介 在本文中&#xff0c;为用户提供了一组Python代码&#xff0c;用于在Zemax和SPEOS之间转换源文件。 有些光源&#xff0c;如 .IES 文件&#xff0c;可在 SPEOS 和 Zemax 中进行…
阅读更多...
计算机网络 | 谈谈TCP的流量控制与拥塞控制

计算机网络 | 谈谈TCP的流量控制与拥塞控制

文章目录一、TCP的流量控制1、利用滑动窗口实现流量控制【⭐⭐⭐】2、如何破解【死锁】局面❓二、TCP的拥塞控制1、拥塞控制的一般原理① 解决网络拥塞的误区② 拥塞控制与流量控制的关系【重点理解✔】2、TCP的拥塞控制方法① 接收窗口【rwnd】与拥塞窗口【cwnd】② 慢开始和拥…
阅读更多...
BPE（Byte-Pair Encoding）简介

BPE（Byte-Pair Encoding）简介

文章目录BPE简介Vocabulary构建Encoding and DecodingBPE简介 BPE是一种数据压缩算法的简单形式&#xff0c;数据中最常见的连续字节对被替换成该数据中不存在的字节。BPE的主要目标就是使用最少的token数目来表示一个corpus 在 A New Algorithm for Data Compression中首次提…
阅读更多...
Spring IOC 容器 Bean 加载过程

Spring IOC 容器 Bean 加载过程

Spring IOC 容器 Bean 加载过程 Spring 对于我们所有的类对象进行了统一抽象&#xff0c;抽象为 BeanDefinition &#xff0c;即 Bean 的定义&#xff0c;其中定义了类的全限定类名、加载机制、初始化方式、作用域等信息&#xff0c;用于对我们要自动装配的类进行生成。 Sprin…
阅读更多...
新版本 | 异步复制、交易日历、自定义状态函数......请查收！

新版本 | 异步复制、交易日历、自定义状态函数......请查收！

大家好~DolphinDB 最新版本近日已经发布&#xff0c;本次的 V2.00.9 与 V1.30.21 新版本推出了很多新功能&#xff0c;并对数据库做了全方位提升&#xff0c;是迄今为止新增功能最多的一次更新。新特性一览我们先来看一看新特性包含哪些方面&#xff1a;1、数据库针对数据安全和…
阅读更多...
管理.模型.SWOT

管理.模型.SWOT

1. SWOT 在企业战略规划中&#xff0c;通过辨析企业自身的竞争优势&#xff08;Strengths&#xff09;、劣势&#xff08;Weaknesses&#xff09;和外部环境为企业带来的机会&#xff08;Opportunities&#xff09;和威胁&#xff08; Threats&#xff09;&#xff0c;企业可制…
阅读更多...
Interview系列 - 05 Java|Iterator迭代器|集合继承体系|Set List Map接口特性|List实现类区别

Interview系列 - 05 Java|Iterator迭代器|集合继承体系|Set List Map接口特性|List实现类区别

文章目录01. 迭代器 Iterator 是什么&#xff1f;02. 迭代器 Iterator 有什么特点&#xff1f;03. 迭代器 Iterator 怎么使用&#xff1f;04. 如何边遍历边移除 Collection 中的元素&#xff1f;05. Iterator 和 ListIterator 有什么区别&#xff1f;06. 数组和集合的区别&…
阅读更多...
Alist ——本地网盘管理器

Alist ——本地网盘管理器

Alist ——本地网盘管理器 一、下载工具 Alist https://github.com/alist-org/alist二、启动登录 进入下载好的文件中&#xff0c;在地址栏输入cmd进入命令行启动 进入命令行输入 alist start启动 记住密码&#xff0c;和端口进入浏览器 输入 &#xff1a;127.0.0.1:5244用…
阅读更多...
java final关键字 详解

java final关键字 详解

概述&#xff1a;作用&#xff1a;细节&#xff1a;演示&#xff1a;总结&#xff1a;一、概述 : final [ˈ faɪnl]&#xff0c;最终的&#xff0c;最后的&#xff0c;决定性的&#xff0c;不可改变的。final作为Java中的一个关键字可以用来修饰类&#xff0c;方法&#xff0c…
阅读更多...
【程序人生】从土木专员到网易测试工程师，薪资翻3倍，他经历了什么？

【程序人生】从土木专员到网易测试工程师，薪资翻3倍，他经历了什么？

转行对于很多人来说&#xff0c;是一件艰难而又纠结的事情&#xff0c;或许缺乏勇气&#xff0c;或许缺乏魄力&#xff0c;或许内心深处不愿打破平衡。可对于我来说&#xff0c;转行是一件不可不为的事情&#xff0c;因为那意味着新的方向、新的希望。我是学工程管理的&#xf…
阅读更多...
京东测试进阶之路：初入测试碎碎念篇

京东测试进阶之路：初入测试碎碎念篇

1、基本的测试用例设计方法 基本的测试用例设计方法&#xff08;边界值分析、等价类划分等&#xff09;。 业务和场景的积累&#xff0c;了解测试需求以及易出现的bug的地方。 多维角度设计测试用例&#xff08;用户、业务流程、异常场景、代码逻辑&#xff09;。 2、需求分析 …
阅读更多...
idea自带maven位置、maven全局环境变量配置，安装jar到本地 mac

idea自带maven位置、maven全局环境变量配置，安装jar到本地 mac

声明&#xff1a;本教程为mac版教程&#xff0c;Windows请路过 idea自带maven3配置全局环境变量 mac电脑maven3位置/Applications/IntelliJ\ IDEA.app/Contents/plugins/maven/lib/maven3配置全局变量,编~/.profile文件&#xff08;没有则新建&#xff09; export MAVEN/App…
阅读更多...
JVM-JMM内存模型（happens-before、volatile）

JVM-JMM内存模型（happens-before、volatile）

前言 由于计算机的存储设备与处理器的运算速度有几个数量级的差距所以现代计算机系统都不得不加入一层读写速度尽可能接近处理器运算速度的高速缓存(Cache)来作为内存与处理器之间的缓冲。 将运算需要使用到的数据复制到缓存中&#xff0c;让运算能快速进行&#xff0c;当运算…
阅读更多...
Day895.MySql误删数据还原方案 -MySQL实战

Day895.MySql误删数据还原方案 -MySQL实战

MySql误删数据还原方案 Hi&#xff0c;我是阿昌&#xff0c;今天学习记录的是关于MySql误删数据还原方案的内容。 传统的高可用架构是不能预防误删数据的&#xff0c;因为主库的一个 drop table 命令&#xff0c;会通过 binlog 传给所有从库和级联从库&#xff0c;进而导致整…
阅读更多...
研报精选230220

研报精选230220

目录 【行业230220国信证券】银行业行业专题&#xff1a;经济复苏中的优质中小银行【行业230220国信证券】汽车行业周报&#xff08;2023年第7周&#xff09;&#xff1a;吉利将发布新品牌“银河” &#xff0c;2022年宇通纯电动客车获欧洲销量冠军【行业230220开源证券】商贸零…
阅读更多...
Java File相关操作

Java File相关操作

文章目录File文件操作IO流处理流缓冲流转换流对象流File文件操作 利用File类来操作。 文件操作中常用到相对目录和绝对路径 package org.File; import java.io.File; public class demo01 { public static void main(String[] args) { try{ File file new File("…
阅读更多...
【Java期末复习】《面向对象程序设计》练习库

【Java期末复习】《面向对象程序设计》练习库

目录 一、单选题 二、填空题 三、程序填空题 1、 super使用--有如下父类和子类的定义&#xff0c;根据要求填写代码 2、简单加法计算器的实现 3、House类 4、矩形类 5、创建一个Box类&#xff0c;求其体积 四、函数题 6-1 求圆面积自定义异常类 6-2 判断一个数列是…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023