最大二叉树

题目详细：LeetCode.654

这道题在题目几乎就说明了解题的思路了：

创建一个根节点，其值为 nums 中的最大值；
递归地在最大值左边的子数组上构建左子树；
递归地在最大值右边的子数组上构建右子树；
返回 nums 构建的最大二叉树。

显而易见，我可以把构建最大二叉树这个大问题，划分为一个个小问题，当每一棵子树都按照上述思路来构建，那么整体就构成了一棵最大二叉树，小问题思路如下：

数组 nums 有三种情况：
- 数组长度为0：说明节点序列为空，返回 null
- 数组长度为1：说明只有一个节点，构建并返回节点
- 数组长度 > 1：找出最大值来构建当前节点
找出nums中的最大值，以及最大值的下标
按照要求，通过最大值的下标来划分构建左右子树的子数组
左子树通过最大值左边的子数组来构建
右子树通过最大值右边的子数组来构建

递归从根节点开始到左右子树构建子树，最后返回构建完成的根节点。

Java解法（递归，深度优先遍历）：

class Solution {
    public int findMaxIndex(int[] nums){
        int res = -1, max = -1;
        for(int i = 0; i < nums.length; i++){
            if(max < nums[i]){
                max = nums[i];
                res = i;
            }
        }
        return res;
    }

    public TreeNode constructMaximumBinaryTree(int[] nums) {
        if(nums.length == 0)
            return null;
        if(nums.length == 1)
            return new TreeNode(nums[0]);
        int max_i = this.findMaxIndex(nums);
        TreeNode root = new TreeNode(nums[max_i]);
        root.left = this.constructMaximumBinaryTree(Arrays.copyOfRange(nums, 0, max_i));
        root.right = this.constructMaximumBinaryTree(Arrays.copyOfRange(nums, max_i+1, nums.length));
        return root;
    }
}

合并二叉树

题目详细：LeetCode.617

通过合并二叉树的过程，不难发现，在合并过程中会出现这4种情况（这里将要合并的树记作 root1 和 root2，让root2合并到root1）：

root1 != null && root2 != null，那么两个节点的值相加，root1.val += root2.val;
root1 == null && root2 != null，左节点为空，那么直接将 root2 合并到 root1 中；
root1 != null && root2 == null，右节点为空，那么无需合并，直接返回左节点
root1 == null && root2 == null，左右节点都为空，无需合并或二叉树已完成合并

递归从根节点到左右子树开始合并子树，最后返回合并完成的根节点（root1）。

Java解法（递归，深度优先遍历）：

class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if(root1 == null){
        // root1 != null && root2 != null
            return root2;
        }else if(root2 == null){
        // root1 == null && root2 != null
            return root1;
        }
        // root1 != null && root2 == null
        root1.val += root2.val;
        root1.left = mergeTrees(root1.left, root2.left);
        root1.right = mergeTrees(root1.right, root2.right);
        return root1;
    }
}

二叉搜索树中的搜索

题目详细：LeetCode.700

二叉搜索树的特点可以简要概括为：

从根节点开始构建一棵二叉树，使其每一棵子树都满足
- 左节点的值 < 父节点的值
- 右节点的值 > 父节点的值
【注意】所以一棵真正的二叉搜索树应满足：
- 左子树上所有的节点值都 < 父节点的值
- 右子树上所有的节点值都 > 父节点的值
那么我们则称这棵树为二叉搜索树

那么这道题要求在二叉搜索树中找到目标值对应的子树，利用二叉搜索树的特点和递归来解题就非常清晰易懂了，在搜索过程中会遇到这3种情况：

节点为空，则二叉树中不到目标值节点，返回null
节点的值 > 目标值，说明目标值只可能在二叉搜索树的右子树出现，递归搜索右子树
节点的值 < 目标值，说明目标值只可能在二叉搜索树的左子树出现，递归搜索左子树
节点的值 = 目标值，说明当前节点就是我们要找的子树的根节点，返回该节点

Java解法（递归，深度优先遍历）：

class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        if(null == root) return null;
        if(val < root.val){
            return searchBST(root.left, val);
        }else if(val > root.val){
            return searchBST(root.right, val);
        }
        // val == root.val
        return root;
    }
}

验证二叉搜索树

题目详细：LeetCode.98

Java（错误的解法，陷进了一个大坑）：

class Solution {
    public boolean isValidBST(TreeNode root) {
        return this.dfs(root.left, root.val, true) && this.dfs(root.right, root.val, false);
    }

    public boolean dfs(TreeNode root, int father_val, boolean is_left){
        if(root == null) return true;
        boolean flag = false;
        if(is_left){
            flag = root.val < father_val
        }else{
            flag = root.val > father_val
        }
        return flag && this.dfs(root.left, root.val, true) && this.dfs(root.right, root.val, false);
    }
}

一开始我发现这道题很简单，不就是根据二叉搜索树的特点来验证一棵二叉树是不是搜索树么，然后就得出结论：

递归验证每一个树的节点是否满足二叉搜索树的特点
二叉搜索树的特点在上一题有讲述，这里就不做赘述了
如果每一个节点都满足，那么则视作整体满足，返回 true

接着写完我就非常自信地提交了答案！很好，错误的测试例子出现了：

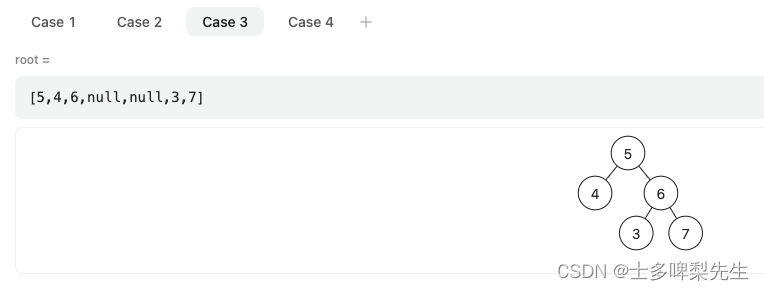
在这里插入图片描述

验证了一下算法，发现到达节点值为3的节点时，应该返回 false，因为假如构建一棵二叉搜索树的话，节点3应该是节点4的左节点才对。

所以：

不能单纯地对每一个节点判断其是否满足左节点 < 父节点，右节点 > 父节点就完事了。
一棵真正的二叉搜索树还需要满足的条件是左子树所有节点 < 父节点，右子树所有节点 > 父节点。

从二叉搜索树的特点，还可以发现其中序遍历序列，是一个递增序列，那么解题方法忽如一夜春风来，千树万树梨花开呀：

解法一：
- 我们可以直接对该二叉树进行中序遍历，获取该树的中序遍历序列；
- 判断该遍历序列是否是递增的，如果是递增序列，则说明该树是二叉搜索树，否则不是。

Java解法（中序遍历，验证二叉搜索树的中序遍历序列是否是递增序列）：

class Solution {
    List<Integer> inorder_list = new ArrayList<>();

    public void dfs(TreeNode root){
        if(root == null) return;
        dfs(root.left);
        inorder_list.add(root.val);
        dfs(root.right);
    }

    public boolean isValidBST(TreeNode root) {
        this.dfs(root);
        int pre = Integer.MIN_VALUE;
        for(int i: this.inorder_list){
            if(pre > i) return false;
            pre = i;
        }
        return true;
    }
}

解法二：
- 从解法一可知，我们可以通过验证中序遍历序列是否递增，进而判断该树是否为二叉搜索树
- 那么我们也可以模拟这一思想，改用迭代的算法能够一边遍历节点，一边处理节点
- 一边迭代遍历二叉树，一边比较与前一个遍历的值，来判断遍历序列是否有序，进而判断该树是否为二叉树

Java解法（中序遍历，模拟，迭代，一边遍历一边比较）：

class Solution {
    public boolean inorder(TreeNode root){
        Stack<TreeNode> stack = new Stack<>();
        if(null != root) stack.push(root);
        TreeNode pre = null;
        while(!stack.isEmpty()){
            TreeNode node = stack.pop();
            if(null != node){
            	// 以右根左的顺序进栈，出栈顺序为左根右
                if(null != node.right) stack.push(node.right);
                stack.push(node);
                stack.push(null);
                if(null != node.left) stack.push(node.left);
            }else{
                node = stack.pop();
                if(null != pre && node.val <= pre.val) return false;
                pre = node;
            }
        }
        return true;
    }

    public boolean isValidBST(TreeNode root) {
        return this.inorder(root);
    }
}