在一条数轴上有 N家商店,它们的坐标分别为 A1∼AN。
现在需要在数轴上建立一家货仓,每天清晨,从货仓到每家商店都要运送商品。
为了提高效率,求把货仓建在何处,可以使得货仓到每家商店的距离之和最小。
输入格式:
第一行输入整数 N。
第二行 N个整数 A1∼AN。
输出格式:
输出一个整数,表示距离之和的最小值。
数据范围
1≤N≤100000,
0≤Ai≤40000
输入样例:
4
6 2 9 1
输出样例:
12
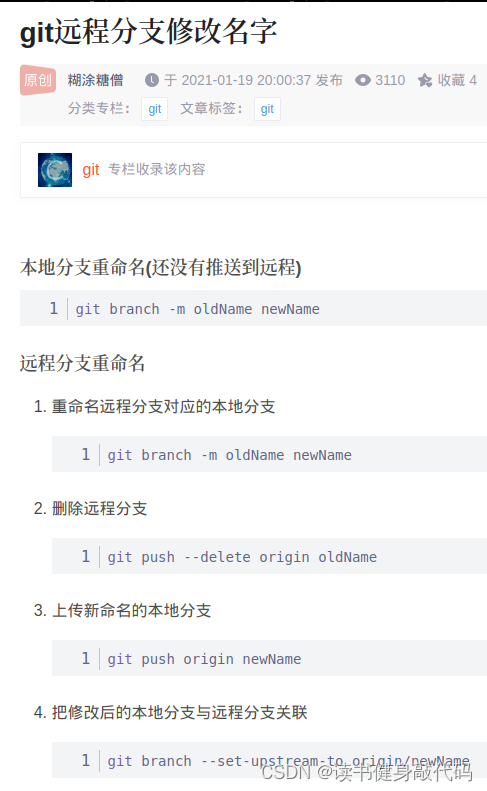
解题思路: 首先对于 a , b (a < b)取一个x数到a,b的距离之和最短,这个距离 dis = | x - a | + |x - b |。
而 | x - a | + |x - b | >= | b - a |。
即 当 x 在,a,b 之间的时候距离之和最短为 b - a。
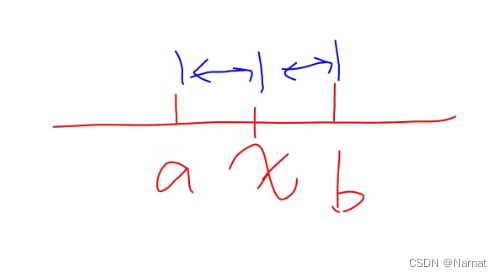
而当 x 取 a,b 左右两边时,距离为 a - x + b - x = a + b - 2x 或者 x - a + x - b = 2x - a - b
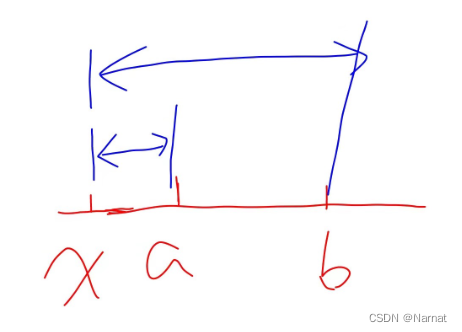
显然后者是没有前者大的,所以对于任意两个数 a,b(a < b)时要想使得到a b的距离之和最短,那么x的位置得取a,b之间(包括 a,b两点)。
而对于a ,b ,c ,d,(a < b < c < d)要想使 x 到他们之间的距离之和最短,首先对于a,d 两点 x 应在a,d之间,在到a,d距离最短的基础上还要使到b,c的距离也最短,由于b,c本身就在a,d之间所以满足前一个条件,所以x在b,c之间取即可(包括b,c点),即取b 或 c 都可。
不管数组有多长以此类推即可。
所以找数组中位数的位置即可。先对数组排序,对偶数组 , 找中间任意两个数即可,对于奇数组找中间一个数即可,不管奇偶用 n / 2 表示中位数位置完全没有问题。
理论成立代码如下:
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int v[] = new int[n];
for(int i = 0; i <n; i ++) v[i] = sc.nextInt();
Arrays.sort(v);
int sum = 0;
for(int i = 0; i < n; i ++) sum = sum + Math.abs(v[i] - v[n / 2]);
System.out.print(sum);
}
}
方法二(把 n / 2 变成 i / 2):
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int v[] = new int[n];
for(int i = 0; i <n; i ++) v[i] = sc.nextInt();
Arrays.sort(v);
int sum = 0;
for(int i = 0; i < n; i ++) sum = sum + Math.abs(v[i] - v[i / 2]);
System.out.print(sum);
}
}