LeetCode 每日一题2347. 最好的扑克手牌

news2024/9/20 7:48:54

Halo，这里是Ppeua。平时主要更新C语言，C++，数据结构算法......感兴趣就关注我吧！你定不会失望。

🌈个人主页：主页链接

🌈算法专栏：专栏链接

我会一直往里填充内容哒！

🌈LeetCode专栏：专栏链接

目前在刷初级算法的LeetBook 。若每日一题当中有力所能及的题目，也会当天做完发出

🌈代码仓库：Gitee链接

🌈点击关注=收获更多优质内容🌈

这道题非常的简单仅分析出返回的优先级就可AC

轮到我了《没营养》（doge 困难题我畏畏缩缩，简单题我重拳出击

题目:

白话讲解:

题解:

代码实现:

完结撒花：

题目:

给你一个整数数组 ranks 和一个字符数组 suit 。你有 5 张扑克牌，第 i 张牌大小为 ranks[i] ，花色为 suits[i] 。

下述是从好到坏你可能持有的 手牌类型 ：

"Flush"：同花，五张相同花色的扑克牌。
"Three of a Kind"：三条，有 3 张大小相同的扑克牌。
"Pair"：对子，两张大小一样的扑克牌。
"High Card"：高牌，五张大小互不相同的扑克牌。

请你返回一个字符串，表示给定的 5 张牌中，你能组成的 最好手牌类型 。

注意：返回的字符串 大小写 需与题目描述相同。
输入：ranks = [13,2,3,1,9], suits = ["a","a","a","a","a"]
输出："Flush"
解释：5 张扑克牌的花色相同，所以返回 "Flush" 。
输入：ranks = [4,4,2,4,4], suits = ["d","a","a","b","c"]
输出："Three of a Kind"
解释：第一、二和四张牌组成三张相同大小的扑克牌，所以得到 "Three of a Kind" 。
注意我们也可以得到 "Pair" ，但是 "Three of a Kind" 是更好的手牌类型。
有其他的 3 张牌也可以组成 "Three of a Kind" 手牌类型。
输入：ranks = [10,10,2,12,9], suits = ["a","b","c","a","d"]
输出："Pair"
解释：第一和第二张牌大小相同，所以得到 "Pair" 。
我们无法得到 "Flush" 或者 "Three of a Kind" 。
ranks.length == suits.length == 5
1 <= ranks[i] <= 13
'a' <= suits[i] <= 'd'
任意两张扑克牌不会同时有相同的大小和花色。

白话讲解:

给出五张手牌的手牌，分析这五张手牌的属性，返回的优先级分别为：五张牌花色相同->三张大小相同的手牌->两张大小相同的手牌->五张大小都不相同的手牌。

题解:

分析题干类型，根据其划分属性我们很容易就能想到用一个东西来记录各种手牌属性出现的次数。

这里根据其数据类型的大小开辟了数组，官解使用hash表

但因为我觉得数组更能体现这个过程（绝对不是因为我不会！好吧就是因为还没看到stl，不想懂个用法就上场

加上题给的数据大小都很小，所以两种方式速度上大差不差。

当然如果数据范围很大，是要用离散化的思想（也就是哈希的原理来开辟数组或者直接使用stl里的hash，否则会造成很严重的空间浪费。

创建两个数组来记录其大小与花色两种属性

首先先遍历花色的suits，因为他优先级最高，若出现一个花色出现五次，则直接返回。

之后遍历手牌大小，这里有一个优化的地方：

若一张手牌大小出现了两次，其已经满足了一种返回条件，但出现三次的优先级更高，此时我们可以记录下是否出现了两次，若之后没有出现三次可以直接返回两次的情况，不需要对数组在进行一次遍历寻找两次的情况。

之后只需要判断是否出现了两次，若无直接返回最差的情况，反之。

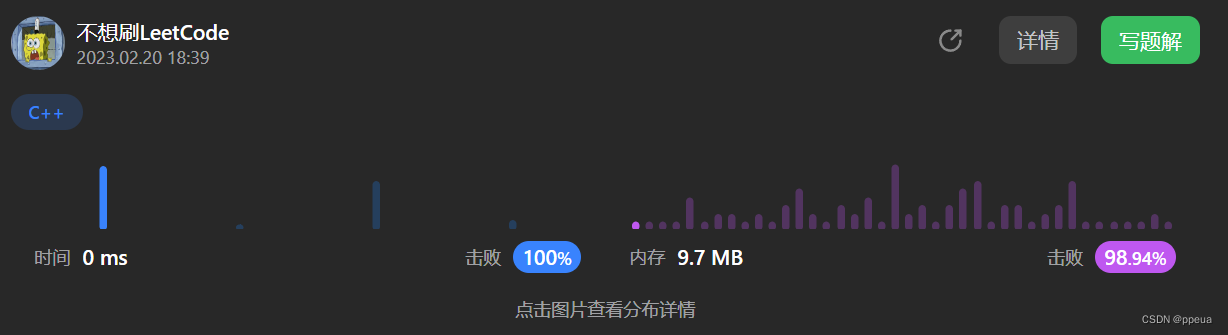
代码实现:

 class Solution {
public:
    string bestHand(vector<int>& ranks, vector<char>& suits) {
        int rank[14]={0},suit[4]={0};
        int flag=0;
        for(auto c:suits)
        {
            suit[c-'a']++;
            if(suit[c-'a']==5)return "Flush";
        }
        for(auto c:ranks)
        {
            rank[c]++;
            if(rank[c]==3)return "Three of a Kind";
            if(rank[c]==2)flag=1;
        }
        return flag==1?"Pair":"High Card";

    }
};