常见优化器整理
一、SGD(随机梯度下降)
-
公式:
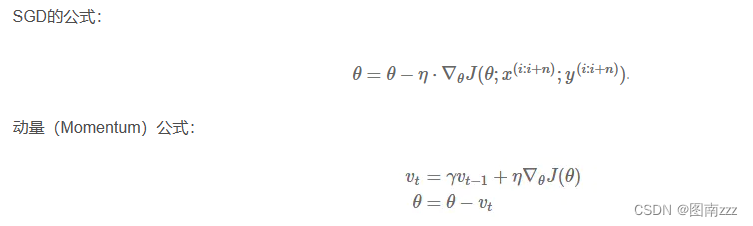
-
经典的mini-batch SGD使用的很多,效果也比较不错,但是存在一部分问题
- 选择恰当的初始学习率很困难
- 学习率调整策略受限于预先制定的调整规则
- 相同的学习率被应用于各个参数
- 高度非凸的误差函数的优化过程,如何避免陷入大量的局部次优解或鞍点
梯度下降遇到的问题
- 很难选择一个合适的学习率,如果学习率太小,将会导致收敛非常缓慢;如果学习率太大,也会阻碍收敛,导致损失函数值在最小值附近波动甚至发散。
- 上述问题可以通过提前定义一个学习速率表,当达到相应轮数或者阈值时根据表改变学习率,但是这样无法适应训练数据本身特征。
- 并且,对于所有参数我们使用同一个学习速率,如果我们的数据是稀疏的或者我们特征具有不同的频率,我们可能不希望将它们更新到同样的程度,并且我们希望对那些出现频率低的特征更新更快。
- 另外在神经网络中,普遍是具有非凸的误差函数,这使得在优化网络过程中,很容易陷入无数的局部最优点,而且更大困难往往也不是陷入局部最优点,而是来自鞍点(也就是在一个维度上其梯度是递增,另一个维度其梯度是递减,而在鞍点处其梯度为0),这些鞍点附近往往被相同误差点所包围,且在任意维度梯度近似为0,所以随机梯度下降很难从这些鞍点逃出。
二、AdaGrad(Adaptive Gradient 自适应梯度)
-
能够对每个不同的参数调整不同的学习率,对频繁变化的参数以更小的步长进行更新,对稀疏的参数以更大的步长进行更新
-
公式
-
增加了分母(梯度平方和的平方根),能够累积个参数的历史梯度评分,频繁更新的梯度累计分母大,步长就小;稀疏的梯度累积的梯度分母小,步长就大。AdaGrad能够自动为不同参数适应不同的学习率(平方根的分母项相当于对学习率α进行了自动调整),大多数的框架实现采用默认学习率α=0.01
-
优势:在数据分布稀疏的场景,能够更好利用稀疏梯度的信息,比标准SGD更容易收敛
-
缺点:分母项不断累积,当时间累积后,会导致学习率收缩到太小导致无法收敛
三、RMSProp
-
结合梯度平方的指数移动平均数来调节学习率变化,能够在不稳定的目标函数情况下很好收敛。
-
公式
-
计算t时刻的梯度

-
计算梯度平方的指数移动平均数(Exponential Moving Average),γ是遗忘因子(指数衰减率),默认设置为0.9
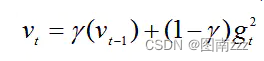
-
梯度更新的时候,与AdaGrad类似,只是更新的梯度平方的期望(指数移动均值),其中ε=10−8,避免除数为0。默认学习率α=0.001。
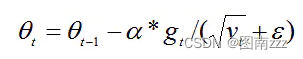
-
-
优势:能够克服AdaGrad梯度急剧减小的问题,再很多应用中都展现出优秀的学习率自适应能力,尤其在不稳定(Non-Stationary)的目标函数下,比基本的SGD、Momentum、AdaGrad表现更良好。
四、Adadelta
-
Adadelta算法可以解决上述问题,其一阶向量跟adagrad一样,二阶参数有所变化:
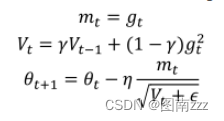
-
二阶参数表达式跟动量表达式相似,引入了参数γ,可以知道二阶动量其实之前所有梯度平方的一个加权平均值,表达式如下:
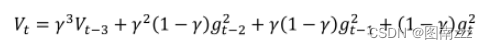
-
从而可以解决AdaGrad带来的分母越来越大的问题
五、Adam(adaptive Moment Estimation自适应矩估计)
-
Adam是一种将动量和Adadelta或RMSprop结合起来的算法,也就引入了两个参数β1和β2,其一阶和二阶动量公式为:
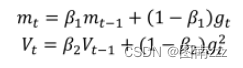
-
但是由于一阶和二阶动量初始训练时很小,接近于0,因为β值很大,于是又引入一个偏差来校正:

-
其中t代表其t次方,所以刚开始训练时,通过除以(1-β)就可以很好修正学习速率,当训练多轮时,分母部分也接近1,又回到了原初始方程,所以最后总的梯度更新方程为:

-
其中β1默认值为0.9,β2默认值为0.999,ε为10-8,Adam集合动量和Adadelata两者的优点,从经验中表明Adam在实际中表现很好,同时与其他自适应学习算法相比,更有优势。