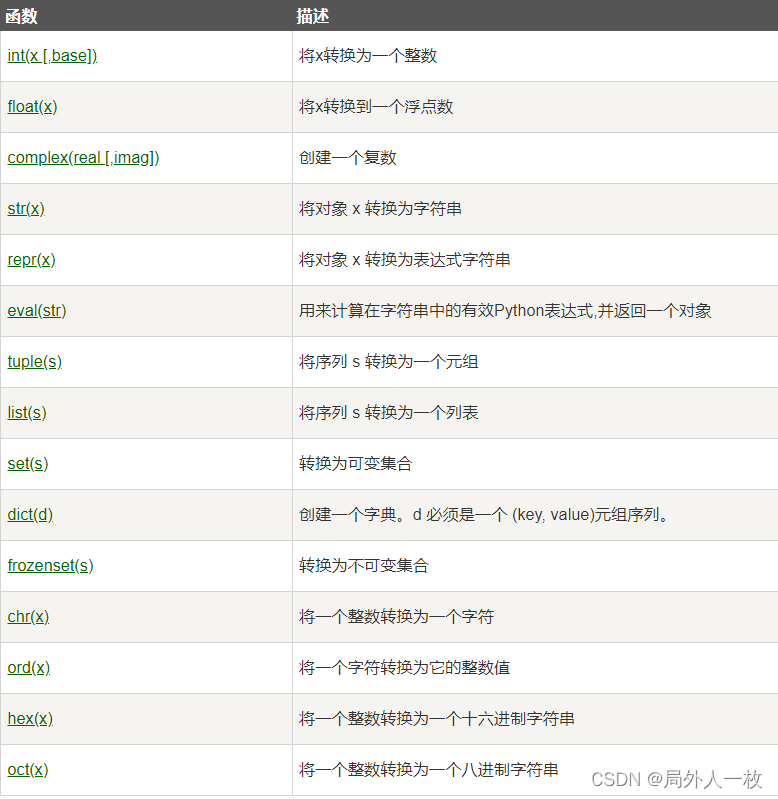
目录

一. 介绍

二. 历史进展分析

三.2维下的堆球问题

四. 3维下的堆球问题

五. 8维与24维下的堆球问题

总结

---

一. 介绍

堆球问题又叫堆球理论、最密堆积、球填充，英文为The Theory Of Sphere Packings。

堆球问题的本质就是填充一堆大小相同的球。要求这些球是刚球，互相之间不能重叠，寻找其最大的密度。关于该密度，简单给一个解释，假设有一个边长为a的立方体的箱子，最大可以放n个体积为v的小球，那么堆球的最大密度即为：

备注：很明显该处例子为三维情况，还可以是四维、五维、······（可以思考下高维下球变成？立方体变成？）。三维寻找最高的堆球密度又被称之为开普勒猜想。

 

二. 历史进展分析

1591年，Thomas Harriot 出版了一本关于各种堆叠问题的研究，并曾最早发展出原子论；

1611年，Johannes Kepler（开普勒）在一篇讲雪花的拉丁语论文中发散出三维下堆球问题的密度上限，但并未给出证明，这便是开普勒猜想。

1831年，高斯证明若球在规则格中进行排列（类似现如今格密码的格点），则开普勒猜想是正确的。这也表明任何反证法都需要寻找不规则的排列方式，实际上，当装球的空间不够大时，确实存在某些不规则排列法密度高于开普勒猜想；

1900年，开普勒猜想被列为希尔伯特的23个问题中的第18个；

1953年，László Fejes Tóth证明任何排列法密度的问题，都可变为有限量的计算过程。这表明至少在原则上，通过穷举法可证明堆球理论的上界；

1958年，英国数学家找到三维空间里任何可能得装球方法上界为78%。我们的目标是将该上界不断缩小，尽量逼近理论上界74%。

1992年，黑尔斯认为可通过一个有着150个变量的方程式的最小值，来找出任何可能装球排法的最大密度。若要寻找每种情况的下界，则需要解超过十万个线性规划问题。

1993年，向武义宣传自己借由几何的方法证明了开普勒猜想，但该证明其实不完善（其实就是不太正确）；

1998年，黑尔斯利用3GB的电脑文案证明，以及250页的注解，宣布证明了开普勒猜想。《数学年报》相关裁判员嘉伯‧费耶斯‧托特利用三年时间，确定该证明99%的可能性正确，因为不能完全确定所有电脑计算的正确性；

2015年，黑尔斯和21位作者共同发表了“开普勒猜想的形式化证明”。该论文借助HOL等自动证明检验软件来确认其正确性的证明，来移出所有剩余的、和证明有效性相关的不确定成分。

2022年，Viazovska因为8维空间和24维空间的堆球工作荣获Fields奖。

三.2维下的堆球问题

杜厄定理是在1890年提出的，该定理表明正六边形排列法（每个球旁边都围着六颗球的排列法）是平面上密度最高的堆球法。

设圆的半径为r，则正六边形的边长为2r，不难运算该正六边形的面积为：

该正六边型内包含3个完整的球（把残缺的球进行拼接），所以总球的面积为：

所以，密度为：

黑尔斯在1999年也曾证明出一个相关的六角蜂巢猜想（若要将二维平面分割成彼此大小相同的区块，则最有效的方法是将之分成由正六边形组成的区块。

四. 3维下的堆球问题

开普勒猜想指出，在三维空间中，堆球的最大密度为：

 

五. 8维与24维下的堆球问题

由英国数学家John Leech在1960年确定，并把该结构称为利奇晶格。2016年，乌克兰数学家Maryna Sergiivna Viazovska将该结果推广到球体填充问题，得出最高密度，8维约3.6%，24维约0.005%。

总结

维度越多，球体填充密度会越来越低，最后无限趋向于0 。

堆球理论历经牛顿、高斯、希尔布特、闵可夫斯基、黑尔斯和Viazovska的研究与推动，堆球理论已经发展成为数论、代数、几何和组合交叉领域的一个重要分支。该理论还可以被应用于格密码，尤其是由Shor, Ajtai, Pipher等人进行的抗量子攻击密码体系研究。