第二十三章 矩阵算法
目录
第二十三章 矩阵算法
●前言
●矩阵算法与深度学习
●一、矩阵相加
●二、矩阵相乘
●三、矩阵转置
●四、稀疏矩阵
●总结
前言
数组与链表都是相当重要的结构化数据类型,也都是典型线性表的应用。线性表用于计算机中的数据存储结构,按照内存存储的方式基本上可以分为以下两种:静态数据结构和动态数据结构。数组类型就是一种典型的静态数据结构,动态数据结构又称为链表。在我前面的算法系列文章都细致的对二者的使用方法做过讲解。
矩阵算法与深度学习
从数学的角度来看,矩阵在计算机中是以二维数组的形式来展现的。在三维图形学中,矩阵也被经常性的使用,因为它可以表示模型数据的投影,扩大,缩小等三维运算。深度学习是目前相当热门的技术和话题,它与机器学习等技术类属于人工智能的一个分支,也是具有层次性的机器学习法。线性代数在深度学习中发挥了它强大的数学能力,在深度学习中我们常常用大量的矩阵运算来提高计算效率。在GPU(图形处理器)的内部,它就是以向量和矩阵元素为基础的,大量的矩阵运算可以分配给数众多的内核同步去进行处理,从而使人工智能领域进入更实用性的阶段。深度学习源自于类神经网络模型,它结合了大量的运算资源和神经网络框架,让机器像人类大脑那样通过大量的数据信息来进行神经网络化的深度学习。就像前几年的人工智能围棋程序AlphaGo就展现出了它的强大生命力。
一、矩阵相加
1.具体情况
矩阵的相加运算较为简单,前提是相加的几个矩阵具有相同的行列数,从而相加后的结果矩阵与原来矩阵的行列数也是相同的。具体如下图所示:
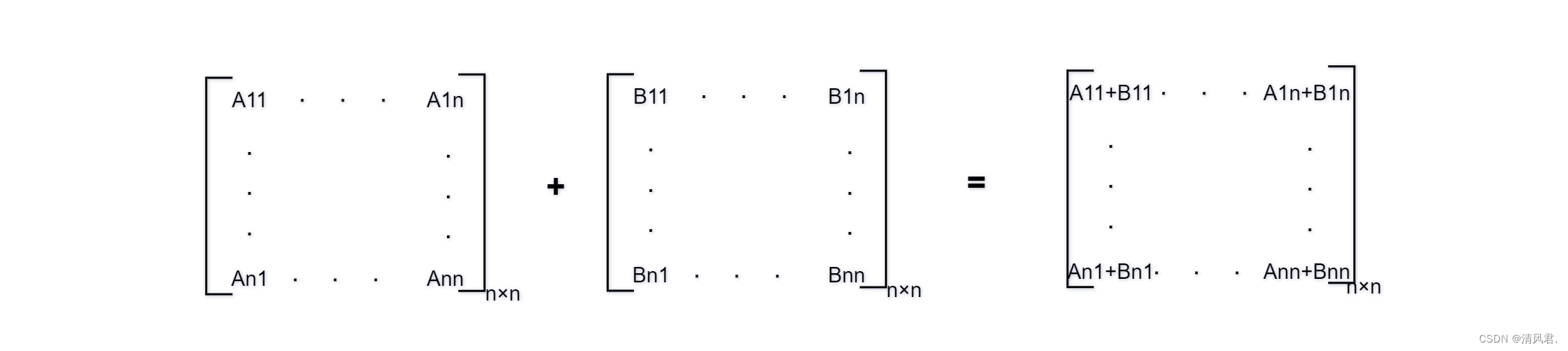
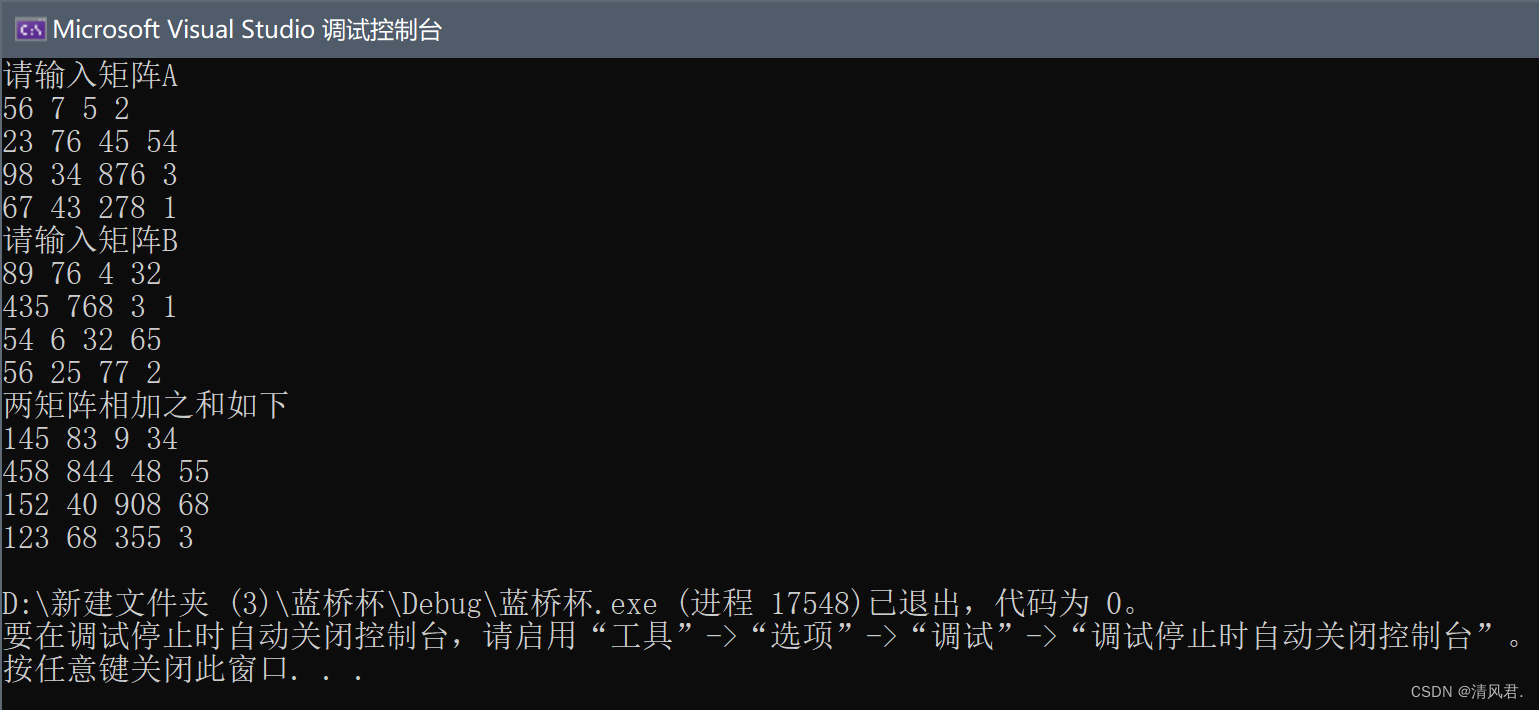
2.范例程序:用程序代码对随机输入的两个矩阵进行相加。
3.代码展示:
#include<iostream>
using namespace std;
#define row 4 //事先声明矩阵的行数
#define col 4 //事先声明矩阵的列数
class matrix {
public:
int A[row][col];
int B[row][col];
int record[row][col];
void matrix_add() {
for (int i = 0; i < row; i++)
for (int j = 0; j < col; j++)
record[i][j] = A[i][j] + B[i][j];
}
void showresult() {
cout << "两矩阵相加之和如下" << endl;
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
cout << record[i][j] << " ";
}
cout << endl;
}
}
};
void text()
{
matrix m;
cout << "请输入矩阵A" << endl;
for (int i = 0; i < row; i++)
for (int j = 0; j < col; j++)
cin >> m.A[i][j];
cout << "请输入矩阵B" << endl;
for (int i = 0; i < row; i++)
for (int j = 0; j < col; j++)
cin >> m.B[i][j];
m.matrix_add();
m.showresult();
}
int main()
{
text();
}4.结果展示:
二、矩阵相乘
1.具体情况
两个矩阵A与B的相乘受到了一些条件的限制。首先必须符合A为一个m×n的矩阵,B为一个n×p的矩阵,A×B后的结果成为一个m×p的矩阵C,具体如下图所示:
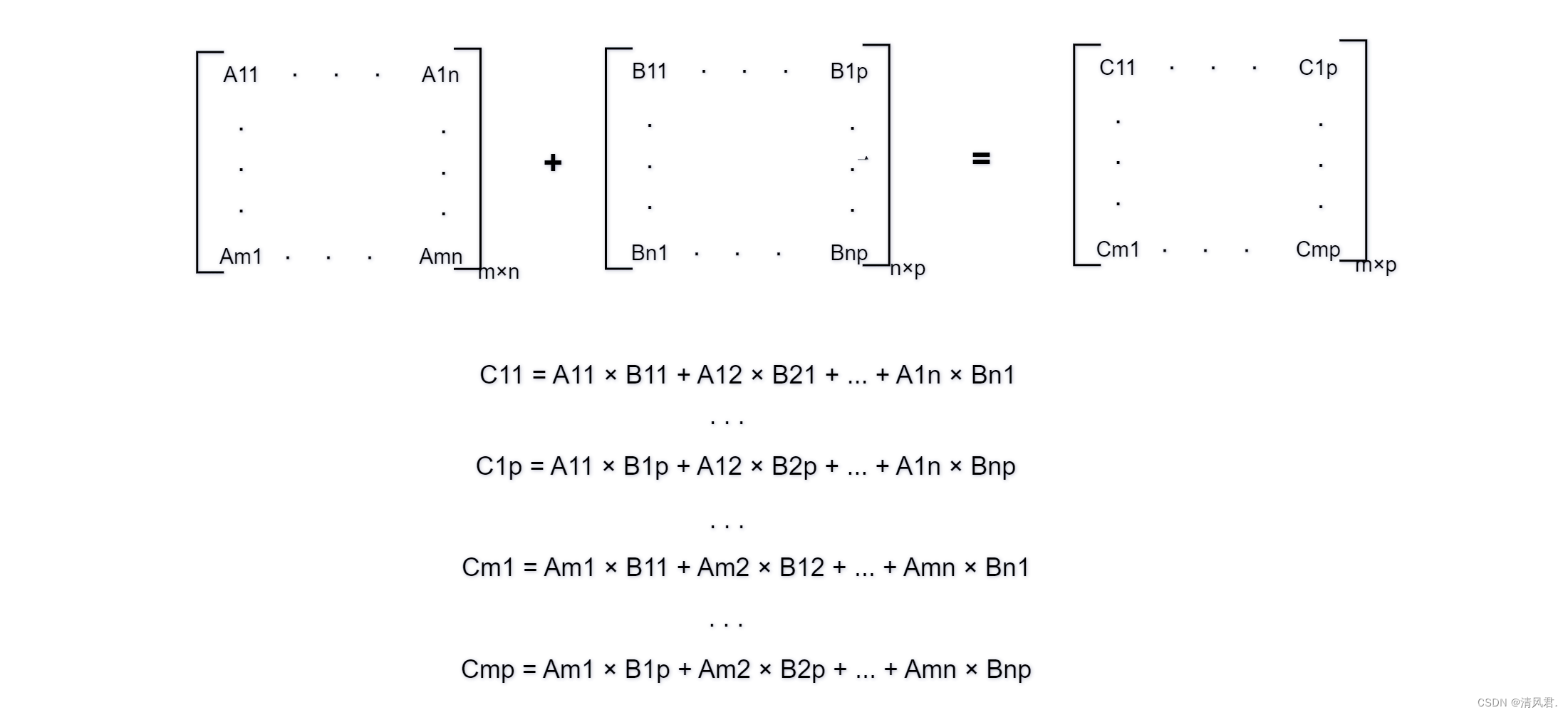
2.范例程序:用程序代码去实现三个随机输入矩阵的相乘。
3.代码展示:
#include<iostream>
using namespace std;
#define row 3 //事先声明矩阵的行数
#define col 3 //事先声明矩阵的列数
class matrix {
public:
int A[row][col];
int B[row][col];
int C[row][col];
int record[row][col];
int sum;
void matrix_mul() {
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
int m = 0,n=0;
record[i][j]=A[i][m] * B[n][j] + A[i][m+1] * B[n+1][j] + A[i][m+2] * B[n+2][j];
}
}
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
int m = 0, n = 0;
record[i][j] = record[i][m] * C[n][j] + record[i][m+1] * C[n+1][j] + record[i][m+2] * C[n+2][j];
}
}
}
void showresult() {
cout << "三矩阵相乘结果如下" << endl;
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
cout << record[i][j] << " ";
}
cout << endl;
}
}
};
void text()
{
matrix m;
cout << "请输入矩阵A" << endl;
for (int i = 0; i < row; i++)
for (int j = 0; j < col; j++)
cin >> m.A[i][j];
cout << "请输入矩阵B" << endl;
for (int i = 0; i < row; i++)
for (int j = 0; j < col; j++)
cin >> m.B[i][j];
cout << "请输入矩阵C" << endl;
for (int i = 0; i < row; i++)
for (int j = 0; j < col; j++)
cin >> m.C[i][j];
m.matrix_mul();
m.showresult();
}
int main()
{
text();
}
4.结果展示:
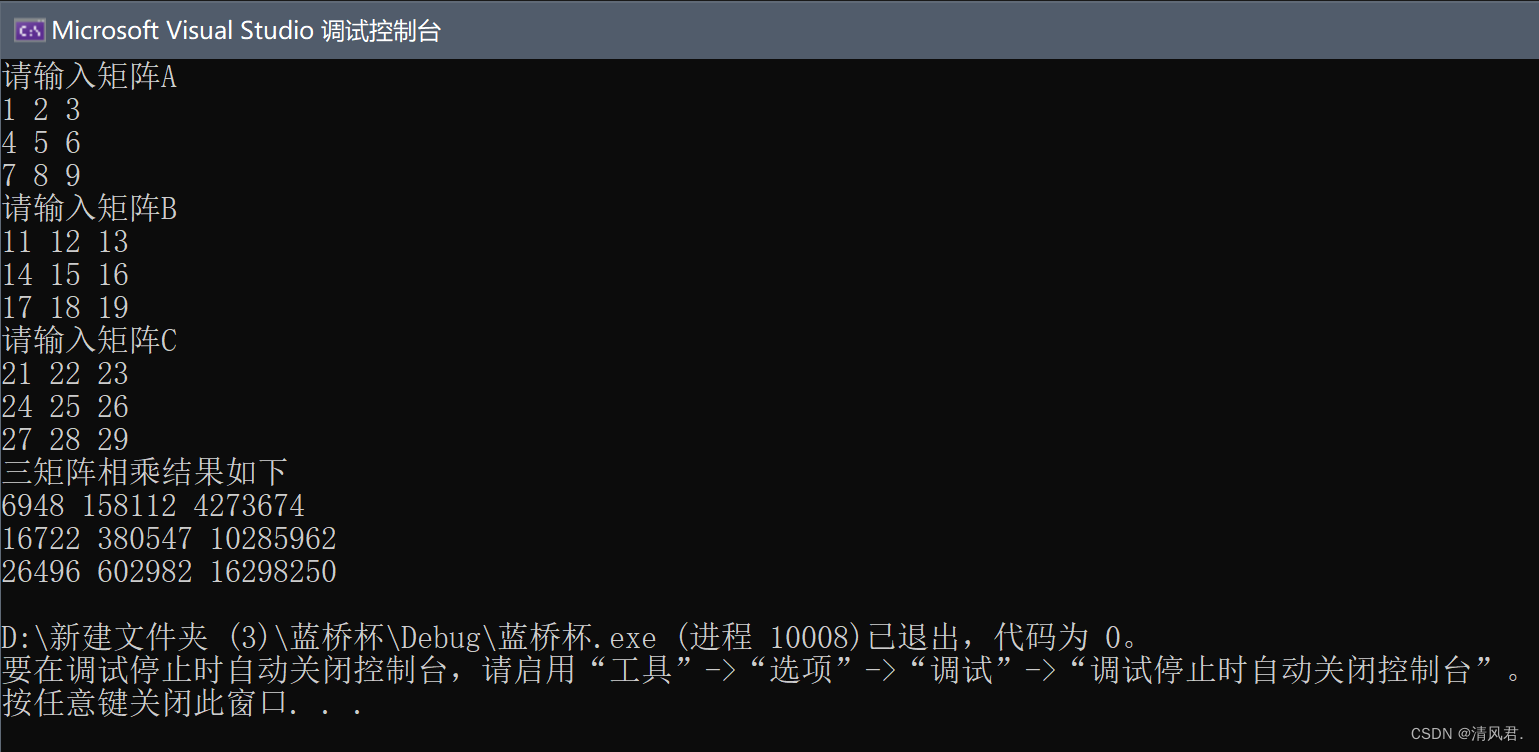
三、矩阵转置
1.具体情况
转置矩阵就是把原矩阵的行坐标元素与列坐标元素进行相互调换。具体如下图所示:

2.范例程序:用程序代码去输出随机输入矩阵的转置矩阵。
3.代码展示:
#include<iostream>
using namespace std;
#define row 4 //事先声明矩阵的行数
#define col 4 //事先声明矩阵的列数
class matrix {
public:
int A[row][col];
int record[row][col];
void matrix_tran() {
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
record[j][i] = A[i][j];
}
}
}
void showresult() {
cout << "输入矩阵的转置结果如下" << endl;
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
cout << record[i][j] << " ";
}
cout << endl;
}
}
};
void text()
{
matrix m;
cout << "请输入矩阵" << endl;
for (int i = 0; i < row; i++)
for (int j = 0; j < col; j++)
cin >> m.A[i][j];
m.matrix_tran();
m.showresult();
}
int main()
{
text();
}4.结果展示:
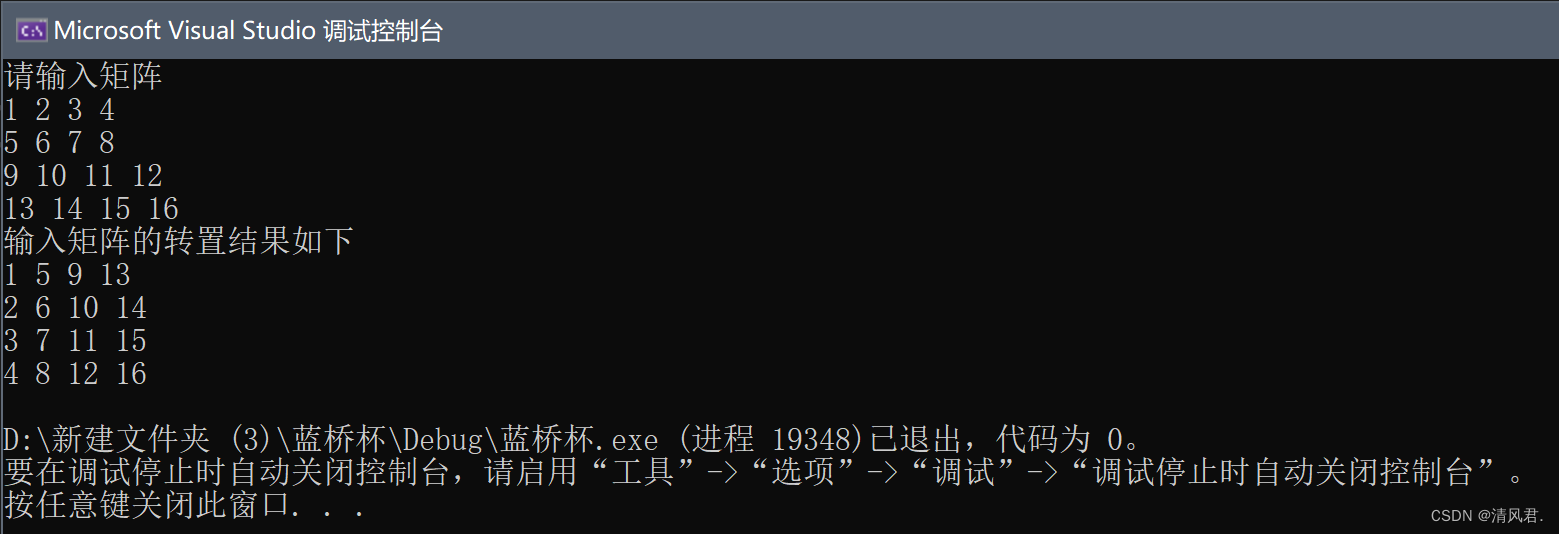
四、稀疏矩阵
1.具体情况
稀疏矩阵就是指一个矩阵中的大部分元素为0的一种特殊矩阵。因为稀疏矩阵中大部分元素都是0,所以实际存储的数据项少,如果在计算机中以传统的方式来存储稀疏矩阵,就会浪费极大的计算机内存。在这里将会用到三项式型的数据结构来存储稀疏矩阵,其中A(0,1):表示该稀疏矩阵的行数;A(0,2):表示该稀疏矩阵的列数;A(0,3):表示此稀疏矩阵中非零项的总数;另外,每一个非零项以(i,j,item-value)来表示。其中i表示此矩阵中非零项所在的行数,j表示非零项所在的列数,item-value表示该非零项的值。具体情况如下图所示:
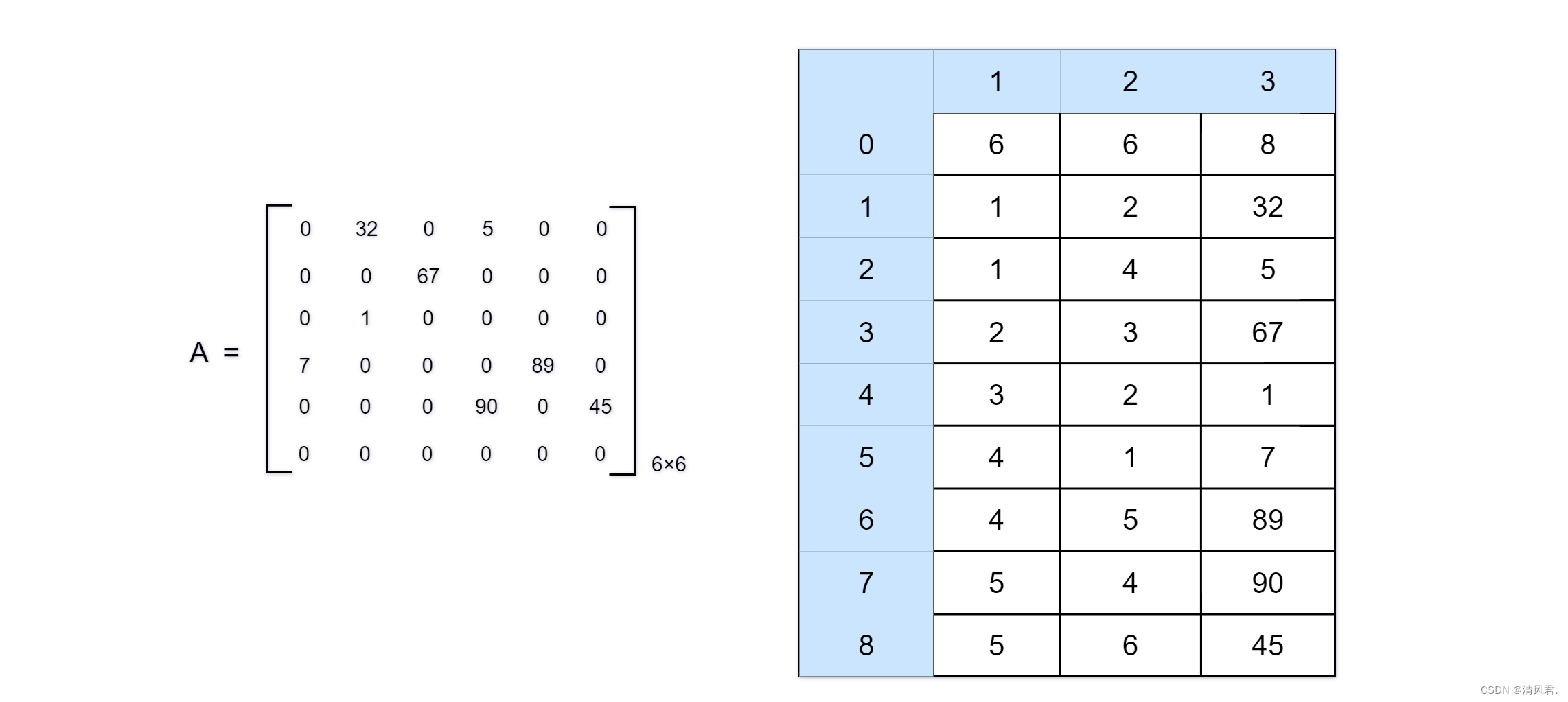
2.范例程序:用程序代码去输出一个随机输入稀疏矩阵的三项式下的压缩结果。
3.代码展示:
#include<iostream>
using namespace std;
#define row 8 //稀疏矩阵的行数
#define col 9 //稀疏矩阵的列数
#define notzero 8 //稀疏矩阵中不为0的数据个数
class matrix {
public:
int sparse[row][col];
int compress[notzero][3];
void matrix_sparse() {
compress[0][0] = row;
compress[0][1] = col;
compress[0][2] = notzero;
cout << "三项式下矩阵的压缩结果如下" << endl;
cout << compress[0][0] << " " << compress[0][1] << " " << compress[0][2] << endl;
for (int i = 0,k=1; i < row; i++,k++) {
int m = 0;
for (int j = 0; j < col; j++) {
if (sparse[i][j] != 0)
{
compress[k][m] = i;
compress[k][m + 1] = j;
compress[k][m + 2] = sparse[i][j];
cout << compress[k][m] <<" "<< compress[k][m + 1] <<" "<< compress[k][m + 2] << endl;
}
}
}
}
};
void text()
{
matrix m;
cout << "请输入稀疏矩阵" << endl;
for (int i = 0; i < row; i++)
for (int j = 0; j < col; j++)
cin >> m.sparse[i][j];
m.matrix_sparse();
}
int main()
{
text();
}
4.结果展示
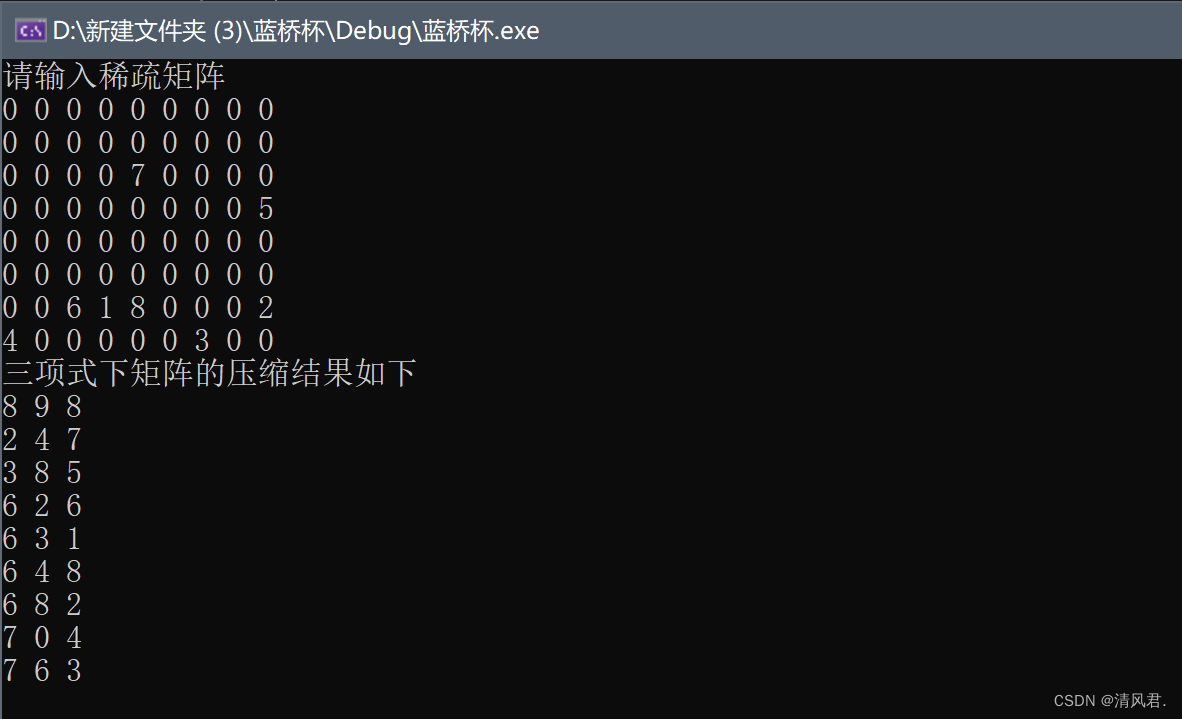
总结
矩阵是高等代数学中的常见工具,在物理学,计算机科学等等的领域它都有着非常重要的应用。在上面我们只介绍了一些简单的矩阵运算实例,其实矩阵的运算和矩阵的类别有很多很多,它们都可以尝试用代码在程序中进行模拟实现。
<您的三连和关注是我最大的动力>
🚀 文章作者:Keanu Zhang 分类专栏:算法之美(C++系列文章)