机器学习笔记之谱聚类——K-Means聚类算法介绍
引言
从本节开始,将介绍聚类任务,本节将介绍 k-Means \text{k-Means} k-Means算法。
回顾:高斯混合模型
高斯混合模型(
Gaussian Mixture Model,GMM
\text{Gaussian Mixture Model,GMM}
Gaussian Mixture Model,GMM)是一种处理聚类任务的常用模型。作为一种概率生成模型,它的概率图结构可表示为如下形式:
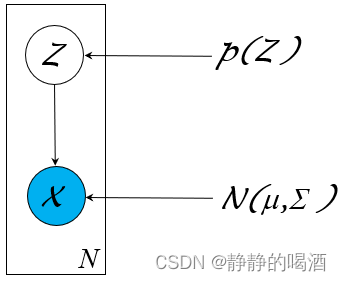
其中隐变量
Z
\mathcal Z
Z是一个离散型随机变量,对应随机变量
X
\mathcal X
X的后验结果服从高斯分布:
Z
∼
Categorical Distribution
(
1
,
2
,
⋯
,
K
)
X
∣
Z
∼
N
(
μ
k
,
Σ
k
)
k
∈
{
1
,
2
,
⋯
,
K
}
\begin{aligned} \mathcal Z & \sim \text{Categorical Distribution}(1,2,\cdots,\mathcal K) \\ \mathcal X & \mid \mathcal Z \sim \mathcal N(\mu_{k},\Sigma_{k}) \quad k \in \{1,2,\cdots,\mathcal K\} \end{aligned}
ZX∼Categorical Distribution(1,2,⋯,K)∣Z∼N(μk,Σk)k∈{1,2,⋯,K}
从生成模型的角度,高斯混合模型对
P
(
X
,
Z
)
\mathcal P(\mathcal X,\mathcal Z)
P(X,Z)进行建模。关于
X
\mathcal X
X的概率密度函数
P
(
X
)
\mathcal P(\mathcal X)
P(X)可表示为如下形式:
其中
P
Z
k
\mathcal P_{\mathcal Z_k}
PZk表示隐变量
Z
\mathcal Z
Z选择离散结果
k
k
k时的概率结果;
μ
Z
k
,
Σ
Z
k
\mu_{\mathcal Z_k},\Sigma_{\mathcal Z_k}
μZk,ΣZk表示对应
X
∣
Z
k
\mathcal X \mid \mathcal Z_k
X∣Zk高斯分布的均值和协方差信息。
P
(
X
)
=
∑
Z
P
(
X
,
Z
)
=
∑
Z
P
(
Z
)
⋅
P
(
X
∣
Z
)
=
∑
k
=
1
K
P
Z
k
⋅
N
(
μ
Z
k
,
Σ
Z
k
)
\begin{aligned} \mathcal P(\mathcal X) & = \sum_{\mathcal Z} \mathcal P(\mathcal X,\mathcal Z) \\ & = \sum_{\mathcal Z} \mathcal P(\mathcal Z) \cdot \mathcal P(\mathcal X \mid \mathcal Z) \\ & = \sum_{k=1}^{\mathcal K}\mathcal P_{\mathcal Z_k} \cdot \mathcal N(\mu_{\mathcal Z_k},\Sigma_{\mathcal Z_k}) \end{aligned}
P(X)=Z∑P(X,Z)=Z∑P(Z)⋅P(X∣Z)=k=1∑KPZk⋅N(μZk,ΣZk)
聚类任务基本介绍
在生成模型综述——监督学习与无监督学习中简单介绍过,聚类( Clustering \text{Clustering} Clustering)任务属于无监督学习( Unsupervised Learning \text{Unsupervised Learning} Unsupervised Learning)任务。无监督学习任务的特点是:样本标签是未知的。而无监督学习的目标是通过学习无标签的样本来揭示数据的内在性质及规律。
而聚类试图将数据集内的样本划分为若干个子集,每个子集称为一个簇( Cluster \text{Cluster} Cluster)。从概率/非概率模型的角度划分,概率模型的典型模型是高斯混合模型;而非概率的聚类模型,其主要代表是 k k k均值算法( k-Means \text{k-Means} k-Means)。
距离计算
在介绍 k-Means \text{k-Means} k-Means算法之前,需要介绍聚类的有效性指标( Vaildity Index \text{Vaildity Index} Vaildity Index)。从直观上描述,在聚类的过程我们更希望物以类聚——相同簇的样本尽可能地彼此相似,不同簇的样本尽可能地不同。
对于两个样本点,通常使用计算它们在样本空间中的距离 来描述两样本之间的相似性程度。样本之间距离越小,样本之间的相似性程度越高,反之同理。
已知两个样本
x
(
i
)
,
x
(
j
)
x^{(i)},x^{(j)}
x(i),x(j)表示如下:
它们均属于
p
p
p维特征空间,即
x
(
i
)
,
x
(
j
)
∈
R
p
x^{(i)},x^{(j)} \in \mathbb R^p
x(i),x(j)∈Rp.
{
x
(
i
)
=
(
x
1
(
i
)
,
x
2
(
i
)
,
⋯
,
x
p
(
i
)
)
T
x
(
j
)
=
(
x
1
(
j
)
,
x
2
(
j
)
,
⋯
,
x
p
(
j
)
)
T
\begin{cases} x^{(i)} = \left(x_1^{(i)},x_2^{(i)},\cdots,x_p^{(i)}\right)^T \\ x^{(j)} = \left(x_1^{(j)},x_2^{(j)},\cdots,x_p^{(j)}\right)^T \end{cases}
⎩
⎨
⎧x(i)=(x1(i),x2(i),⋯,xp(i))Tx(j)=(x1(j),x2(j),⋯,xp(j))T
关于描述样本
x
(
i
)
,
x
(
j
)
x^{(i)},x^{(j)}
x(i),x(j)之间的距离,最常用的方法是明可夫斯基距离(
Minkowski Distance
\text{Minkowski Distance}
Minkowski Distance):
其中参数
m
≥
1
m \geq 1
m≥1.
Dist
mk
(
x
(
i
)
,
x
(
j
)
)
=
(
∑
k
=
1
p
∣
x
k
(
i
)
−
x
k
(
j
)
∣
m
)
1
m
\text{Dist}_{\text{mk}}(x^{(i)},x^{(j)}) = \left(\sum_{k=1}^p \left|x_k^{(i)} - x_k^{(j)}\right|^m\right)^{\frac{1}{m}}
Distmk(x(i),x(j))=(k=1∑p
xk(i)−xk(j)
m)m1
当
m
=
2
m=2
m=2时的明可夫斯基距离即欧几里得距离(
Euclidean Distance
\text{Euclidean Distance}
Euclidean Distance),也称欧式距离:
Dist
ed
(
x
(
i
)
,
x
(
j
)
)
=
(
∑
k
=
1
p
∣
x
k
(
i
)
−
x
k
(
j
)
∣
2
)
1
2
=
∑
k
=
1
p
∣
x
k
(
i
)
−
x
k
(
j
)
∣
2
=
∣
∣
x
(
i
)
−
x
(
j
)
∣
∣
2
\begin{aligned} \text{Dist}_{\text{ed}}(x^{(i)},x^{(j)}) & = \left(\sum_{k=1}^p \left|x_k^{(i)} - x_k^{(j)}\right|^2\right)^{\frac{1}{2}} \\ & = \sqrt{\sum_{k=1}^p \left|x_k^{(i)} - x_k^{(j)}\right|^2} \\ & = \left|\left|x^{(i)} - x^{(j)}\right|\right|_2 \end{aligned}
Disted(x(i),x(j))=(k=1∑p
xk(i)−xk(j)
2)21=k=1∑p
xk(i)−xk(j)
2=
x(i)−x(j)
2
当
m
=
1
m=1
m=1时的明可夫斯基距离即曼哈顿距离(
Manhattan Distance
\text{Manhattan Distance}
Manhattan Distance):
Dist
man
=
∑
k
=
1
p
∣
x
k
(
i
)
−
x
k
(
j
)
∣
=
∣
∣
x
(
i
)
−
x
(
j
)
∣
∣
1
\begin{aligned} \text{Dist}_{\text{man}} & = \sum_{k=1}^p \left|x_k^{(i)} - x_k^{(j)}\right| \\ & = \left|\left|x^{(i)} - x^{(j)}\right|\right|_1 \end{aligned}
Distman=k=1∑p
xk(i)−xk(j)
=
x(i)−x(j)
1
k-Means \text{k-Means} k-Means算法介绍
给定一个样本集合
D
=
{
x
(
1
)
,
x
(
2
)
,
⋯
,
x
(
N
)
}
\mathcal D = \{x^{(1)},x^{(2)},\cdots,x^{(N)}\}
D={x(1),x(2),⋯,x(N)},并设定簇的数量
C
=
{
C
1
,
C
2
,
⋯
,
C
K
}
\mathcal C = \{C_1,C_2,\cdots,C_{\mathcal K}\}
C={C1,C2,⋯,CK},那么目标函数可描述成:对所有的簇,各簇内样本到均值向量之间的距离之和:
{
E
=
∑
k
=
1
K
∑
x
∈
C
k
Dist
(
x
,
μ
k
)
μ
k
=
1
∣
C
k
∣
∑
x
∈
C
k
x
\begin{cases} \mathbb E = \sum_{k=1}^{\mathcal K} \sum_{x \in C_k} \text{Dist}(x,\mu_k) \\ \mu_{k} = \frac{1}{|C_k|} \sum_{x \in C_k} x \end{cases}
{E=∑k=1K∑x∈CkDist(x,μk)μk=∣Ck∣1∑x∈Ckx
其中
μ
k
\mu_k
μk表示簇
C
k
C_k
Ck的均值向量。观察上式,
∑
x
∈
C
k
Dist
(
x
,
μ
k
)
\sum_{x \in C_k} \text{Dist}(x,\mu_k)
∑x∈CkDist(x,μk)描述了簇
C
k
C_k
Ck内样本围绕
μ
k
\mu_k
μk的紧密程度:
- 如果 ∑ x ∈ C k Dist ( x , μ k ) \sum_{x \in C_k} \text{Dist}(x,\mu_k) ∑x∈CkDist(x,μk)较小,那么簇 C k C_k Ck内样本的紧密程度就高;
- 同理,如果 ∑ k = 1 K ∑ x ∈ C k Dist ( x , μ k ) \sum_{k=1}^{\mathcal K} \sum_{x \in C_k} \text{Dist}(x,\mu_k) ∑k=1K∑x∈CkDist(x,μk)小,意味着各个簇内样本的紧密程度都较高,从而达到样本分类的目的。
如果想要通过这种方式去寻找各簇对应的
μ
k
\mu_k
μk,这明显是一个
NP-Hard
\text{NP-Hard}
NP-Hard问题:均值向量
μ
k
\mu_k
μk并不是某个真实的样本点,因而它有无穷多种可能;虽然在给定样本的条件下,各簇对应的
μ
k
\mu_k
μk是客观存在的,但相应寻找的代价是极高的。
假设在当前样本条件下,找到了最优的簇对应的
μ
k
\mu_k
μk,但样本自身是存在噪声的,如果新加入样本进来,可能会使
μ
k
\mu_k
μk产生变化。
那么
k-Means
\text{k-Means}
k-Means方法采用贪心策略,通过迭代的方式去近似求解
E
=
∑
k
=
1
K
∑
x
∈
C
k
Dist
(
x
,
μ
k
)
\mathbb E = \sum_{k=1}^{\mathcal K} \sum_{x \in C_k} \text{Dist}(x,\mu_k)
E=∑k=1K∑x∈CkDist(x,μk)的最小值。下面通过实例使用
k-Means
\text{k-Means}
k-Means算法进行近似求解。
示例转载自K-means 算法【基本概念篇】非常感谢,侵删。
k-Means \text{k-Means} k-Means算法示例
已知包含二维特征的数据集合
D
\mathcal D
D表示如下,并针对该集合使用
k-Means
\text{k-Means}
k-Means算法执行聚类任务:
D
=
{
(
2
,
10
)
,
(
2
,
5
)
,
(
8
,
4
)
,
(
5
,
8
)
,
(
7
,
5
)
,
(
6
,
4
)
,
(
1
,
2
)
,
(
4
,
9
)
}
\mathcal D = \{(2,10),(2,5),(8,4),(5,8),(7,5),(6,4),(1,2),(4,9)\}
D={(2,10),(2,5),(8,4),(5,8),(7,5),(6,4),(1,2),(4,9)}
对应二维图像表示如下:
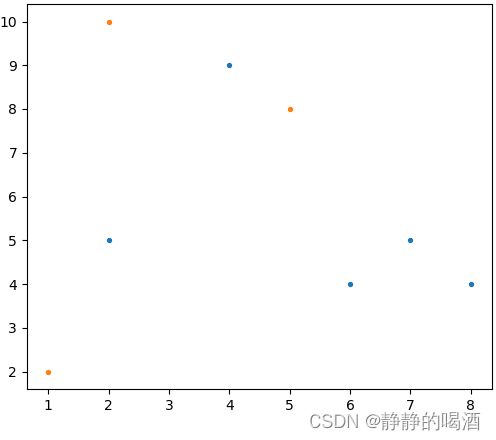
- 假设将上述集合内的样本点划分成三类,因此需要选择三个类对应的初始中心。这里我们从集合中随机选择样本点作为初始中心(上图中的橙色样本点):
当然,并不是说‘初始中心’就必须在样本中进行选择,实际上只要是样本空间中任意点都可作为初始中心。
μ 1 ( i n i t ) = ( 2 , 10 ) μ 2 ( i n i t ) = ( 5 , 8 ) μ 3 ( i n i t ) = ( 1 , 2 ) \mu_1^{(init)} = (2,10)\quad \mu_2^{(init)} = (5,8)\quad \mu_3^{(init)} = (1,2) μ1(init)=(2,10)μ2(init)=(5,8)μ3(init)=(1,2) - 对两样本点之间的距离
Dist
(
x
(
i
)
,
x
(
j
)
)
;
x
(
i
)
,
x
(
j
)
∈
D
\text{Dist}(x^{(i)},x^{(j)});x^{(i)},x^{(j)} \in \mathcal D
Dist(x(i),x(j));x(i),x(j)∈D进行定义。由于样本比较简单,这里直接定义为曼哈顿距离:
ρ [ x ( i ) , x ( j ) ] = ∣ x 1 ( i ) − x 1 ( j ) ∣ + ∣ x 2 ( i ) − x 2 ( j ) ∣ { x ( i ) = ( x 1 ( i ) , x 2 ( i ) ) T x ( j ) = ( x 1 ( j ) , x 2 ( j ) ) T \rho[x^{(i)},x^{(j)}] = \left|x_1^{(i)} - x_1^{(j)}\right| + \left|x_2^{(i)} - x_2^{(j)}\right| \quad \begin{cases} x^{(i)} = (x_1^{(i)},x_2^{(i)})^T \\ x^{(j)} = (x_1^{(j)},x_2^{(j)})^T \end{cases} ρ[x(i),x(j)]= x1(i)−x1(j) + x2(i)−x2(j) {x(i)=(x1(i),x2(i))Tx(j)=(x1(j),x2(j))T - 定义完毕后,将所有样本点分别与三个初始中心计算曼哈顿距离。具体结果表示如下:
示例:样本点( 5 , 8 ) (5,8) (5,8)与初始中心( 2 , 10 ) (2,10) (2,10)之间的曼哈顿距离
ρ = ∣ 5 − 2 ∣ + ∣ 8 − 10 ∣ = 5 \rho = |5-2| + |8 - 10| = 5 ρ=∣5−2∣+∣8−10∣=5
选择距离最小的初始中心,并划分至该初始中心对应的簇。
| SamplePoint/InitialCenter \text{SamplePoint/InitialCenter} SamplePoint/InitialCenter | μ 1 ( i n i t ) : ( 2 , 10 ) \mu_1^{(init)}:(2,10) μ1(init):(2,10) | μ 2 ( i n i t ) : ( 5 , 8 ) \mu_2^{(init)}:(5,8) μ2(init):(5,8) | μ 3 ( i n i t ) : ( 1 , 2 ) \mu_3^{(init)}:(1,2) μ3(init):(1,2) | ClusterResult \text{ClusterResult} ClusterResult |
|---|---|---|---|---|
| ( 2 , 10 ) (2,10) (2,10) | 0 0 0 | 5 5 5 | 9 9 9 | 1 1 1 |
| ( 2 , 5 ) (2,5) (2,5) | 5 5 5 | 6 6 6 | 4 4 4 | 3 3 3 |
| ( 8 , 4 ) (8,4) (8,4) | 12 12 12 | 7 7 7 | 9 9 9 | 2 2 2 |
| ( 5 , 8 ) (5,8) (5,8) | 5 5 5 | 0 0 0 | 10 10 10 | 2 2 2 |
| ( 7 , 5 ) (7,5) (7,5) | 10 10 10 | 5 5 5 | 9 9 9 | 2 2 2 |
| ( 6 , 4 ) (6,4) (6,4) | 10 10 10 | 5 5 5 | 7 7 7 | 2 2 2 |
| ( 1 , 2 ) (1,2) (1,2) | 9 9 9 | 10 10 10 | 0 0 0 | 3 3 3 |
| ( 4 , 9 ) (4,9) (4,9) | 3 3 3 | 2 2 2 | 10 10 10 | 2 2 2 |
至此,得到了第一次迭代产生的聚类结果表示如下:
{
Cluster 1:
(
2
,
10
)
Cluster 2:
(
8
,
4
)
,
(
5
,
8
)
,
(
7
,
5
)
,
(
6
,
4
)
,
(
4
,
9
)
Cluster 3:
(
2
,
5
)
,
(
1
,
2
)
\begin{cases} \text{Cluster 1: }(2,10) \\ \text{Cluster 2: }(8,4),(5,8),(7,5),(6,4),(4,9) \\ \text{Cluster 3: }(2,5),(1,2) \\ \end{cases}
⎩
⎨
⎧Cluster 1: (2,10)Cluster 2: (8,4),(5,8),(7,5),(6,4),(4,9)Cluster 3: (2,5),(1,2)
-
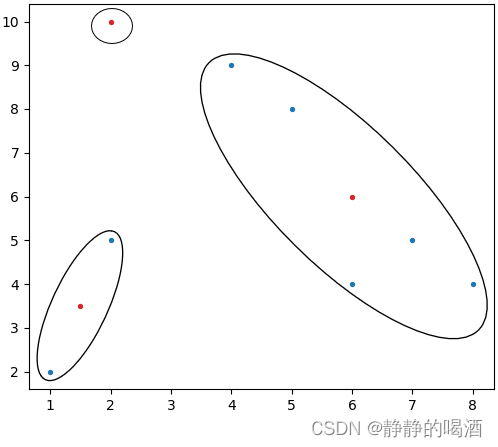
基于第一次迭代,重新计算每个聚类的中心,并替换初始中心:
- Cluster 1: \text{Cluster 1: } Cluster 1: 本次聚类中,该类样本点只有1个,因而新的聚类中心就是它自身;
- Cluster 2: ( 6 , 6 ) ⇐ { x ˉ 1 = ( 4 + 5 + 6 + 7 + 8 ) / 5 = 6 x ˉ 2 = ( 4 + 4 + 5 + 8 + 9 ) / 5 = 6 \text{Cluster 2: } (6,6) \Leftarrow \begin{cases} \bar x_1 = (4+5+6+7+8) / 5 = 6 \\ \bar x_2 = (4+4+5+8+9) / 5 = 6\end{cases} Cluster 2: (6,6)⇐{xˉ1=(4+5+6+7+8)/5=6xˉ2=(4+4+5+8+9)/5=6
- Cluster 3: ( 1.5 , 3.5 ) ⇐ { ( 2 + 1 ) / 2 = 1.5 ( 5 + 2 ) / 2 = 3.5 \text{Cluster 3: }(1.5,3.5) \Leftarrow \begin{cases} (2 + 1)/2 = 1.5 \\ (5 + 2)/2 = 3.5 \end{cases} Cluster 3: (1.5,3.5)⇐{(2+1)/2=1.5(5+2)/2=3.5
此时,基于替换中心的样本空间以及聚类区域表示如下(红色样本点表示第一次迭代后的新聚类中心):
-
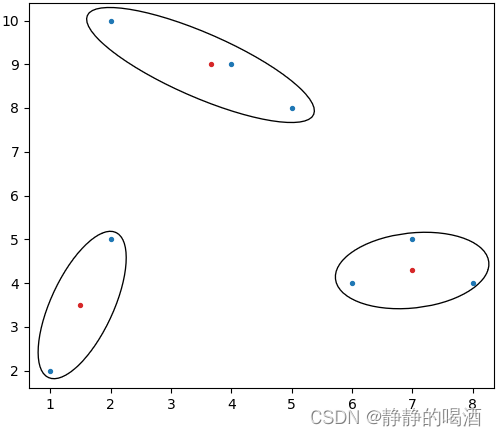
重复执行上述步骤,可以得到新的聚类中心以及对应的簇。直到聚类中心不再发生变化,这意味着:在迭代过程中,通过计算聚类中心所产生的簇内部的样本点已经稳定,不再发生变化。此时即可停止算法:
k-Means \text{k-Means} k-Means算法与高斯混合模型的关系
从上面的迭代过程中,可以发现:整个计算过程与概率没有明显的关联关系。我们仅仅在迭代过程中执行了计算距离并比较大小、更新聚类中心这两种操作。
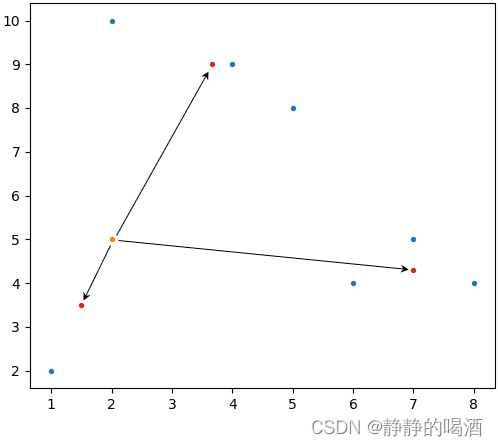
但从单个样本点的角度,可以将其视作高斯混合模型的一种描述。以样本点
(
2
,
5
)
(2,5)
(2,5)为例,对该样本到各聚类中心之间的距离进行计算,并将其映射至(0,1)区间:
注意:这里的箭头表示的是‘欧式距离’,而不是曼哈顿距离。这里仅表示一个指向,不要被误导。
注意:距离数值越小的,映射的结果越大。这意味着样本点与该聚类中心对应的簇关联更加密切。因而这里使用的标准化方法表示如下。其中
N
N
N表示簇的个数;
SumDistance
\text{SumDistance}
SumDistance表示样本到所有聚类中心的
ManhattanDistance
\text{ManhattanDistance}
ManhattanDistance之和。
MappingResult
=
1
N
−
1
(
1
−
ManhattanDistance
SumDistance
)
\text{MappingResult} = \frac{1}{N - 1}(1 - \frac{\text{ManhattanDistance}}{\text{SumDistance}})
MappingResult=N−11(1−SumDistanceManhattanDistance)
这里的标准化方法仅仅描述映射后的大小关系,严格来说并不准确。这里提出一种函数
Softmax
(
1
ManhanttanDistance
)
\text{Softmax}(\frac{1}{\text{ManhanttanDistance}})
Softmax(ManhanttanDistance1)作为参考。
| ManhattanDistance \text{ManhattanDistance} ManhattanDistance | MappingResult \text{MappingResult} MappingResult | |
|---|---|---|
| ( 1.5 , 3.5 ) (1.5,3.5) (1.5,3.5) | 2 2 2 | 0.4253 0.4253 0.4253 |
| ( 7 , 4.3 ) (7,4.3) (7,4.3) | 5.7 5.7 5.7 | 0.2868 0.2868 0.2868 |
| ( 3.67 , 9 ) (3.67,9) (3.67,9) | 5.67 5.67 5.67 | 0.2879 0.2879 0.2879 |
观察上述表格的
MappingResult
\text{MappingResult}
MappingResult,完全可以将这一组数值
P
(
Z
)
=
[
0.4253
,
0.5868
,
0.2879
]
\mathcal P(\mathcal Z) = [0.4253,0.5868,0.2879]
P(Z)=[0.4253,0.5868,0.2879]看作是一个概率分布。该概率分布中概率值最大的是对应聚类中心
(
1.5
,
3.5
)
(1.5,3.5)
(1.5,3.5)对应的簇结果。
另一种思路在于:此时的聚类中心已经不是样本点了,此时的聚类中心在样本空间中已经没有任何实际意义,也符合隐变量的描述。
而样本点在给定聚类中心 Z \mathcal Z Z的条件下,那么样本点 x ( i ) ∣ Z x^{(i)} \mid \mathcal Z x(i)∣Z服从高斯分布。因为该样本点距离聚类中心越近,意味着它从该簇中生成的概率越高。因而可将 k-Means \text{k-Means} k-Means视作一种基于高斯混合模型思想的硬划分模型( Hard-GMM \text{Hard-GMM} Hard-GMM)。
k-Means \text{k-Means} k-Means算法的缺陷
虽然 k-Means \text{k-Means} k-Means算法简单,但它同样存在缺陷:
- 我们需要手动添加聚类数量。这需要对样本信息有一定程度的了解,聚类数量的选择对聚类结果的影响是巨大的;
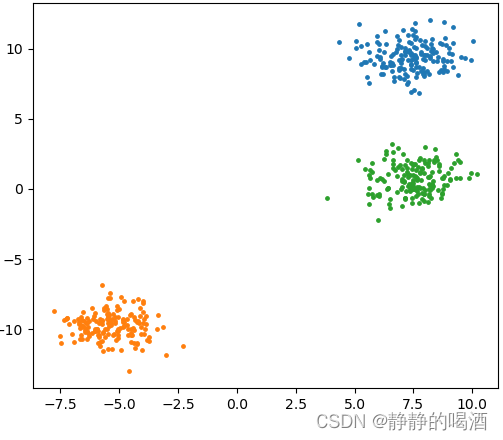
- 它对于聚类分布紧密( Compactness \text{Compactness} Compactness)的样本集合有不错的聚类效果,如簇是凸形状( Convex \text{Convex} Convex)这种类似云团状的分布结构:
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn import cluster
n_samples = 500
colors = ["tab:blue","tab:orange","tab:green"]
blobs = datasets.make_blobs(n_samples=n_samples, random_state=8)
X,y = blobs
KMeans = cluster.MiniBatchKMeans(n_clusters=3)
KMeans.fit(X)
yPred = KMeans.predict(X)
for _,(XElement,yPredElement) in enumerate(zip(X,yPred)):
plt.scatter(XElement[0],XElement[1],color=colors[yPredElement],s=5)
plt.show()
返回结果如下:
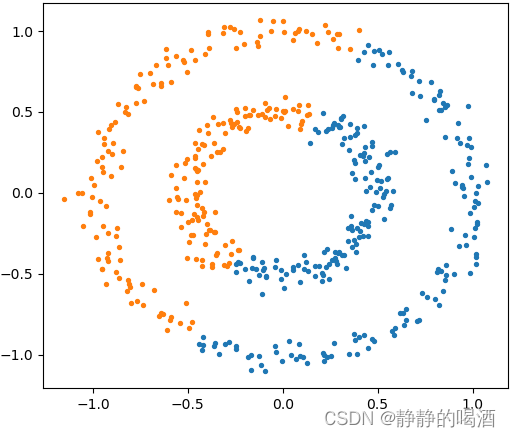
但针对连通性(
Connectivity
\text{Connectivity}
Connectivity)簇分布,它的聚类结果可能并不漂亮:
我们原本希望将大圆与小圆中的样本划分开来;不仅k-Means出现这样的现象,高斯混合模型同样会出现这种现象。
blobs = datasets.make_circles(n_samples=n_samples, factor=0.5, noise=0.05)
关于这种结构,在核方法思想与核函数介绍中提到过,使用核方法 +
k-Means
\text{k-Means}
k-Means的方式进行处理,但这种方式同样因维度增加而可能出现维度诅咒/维度惩罚(
Curse of Dimensionary
\text{Curse of Dimensionary}
Curse of Dimensionary)的风险。因此,针对类似连通类型的簇分布,
k-Means
\text{k-Means}
k-Means并不可取。
下一节从
k-Means
\text{k-Means}
k-Means的缺陷开始,介绍谱聚类(
Spectral Clusting
\text{Spectral Clusting}
Spectral Clusting)。
相关参考:
机器学习-谱聚类(1)-背景介绍
K-means 算法【基本概念篇】
Sklearn
\text{Sklearn}
Sklearn中文文档——K-means
机器学习——周志华著


![[ 对比学习篇 ] 经典网络模型 —— Contrastive Learning](https://img-blog.csdnimg.cn/efd2df2692f540e3bca5e89c2c9e7660.png#pic_center)