1.C4.5算法
C4.5算法与ID3相似,在ID3的基础上进行了改进,采用信息增益比来选择属性。ID3选择属性用的是子树的信息增益,ID3使用的是熵(entropy, 熵是一种不纯度度量准则),也就是熵的变化值,而C4.5用的是信息增益率。
2.信息增益率
在ID3算法中,显然属性的取值越多,信息增益越大。为了避免属性取值个数的影响,C4.5算法从候选划分中找出信息增益高于平均水平的属性,再从中选出信息增益率(用信息增益除以该属性本身的固有值(Intrinsic value)最高的分类作为分裂规则。信息增益比本质就是在信息增益的基础之上乘上一个惩罚参数。特征个数较多时,惩罚参数较小;特征个数较少时,惩罚参数较大。信息增益比就等于惩罚参数 * 信息增益。
2-1 信息增益率
信息增益率:增益率是用前面的信息增益Gain(D, a)和属性a对应的"固有值"(intrinsic value)的比值来共同定义的。属性 a 的可能取值数目越多(即 V 越大),则 IV(a) 的值通常会越大。
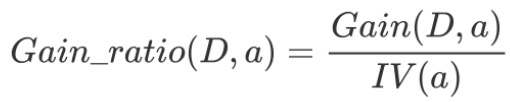
![]()
2-2 案例
根据‘天气’,‘温度’,‘湿度’,‘风速’四个属性判断活动是否进行(进行、取消)。
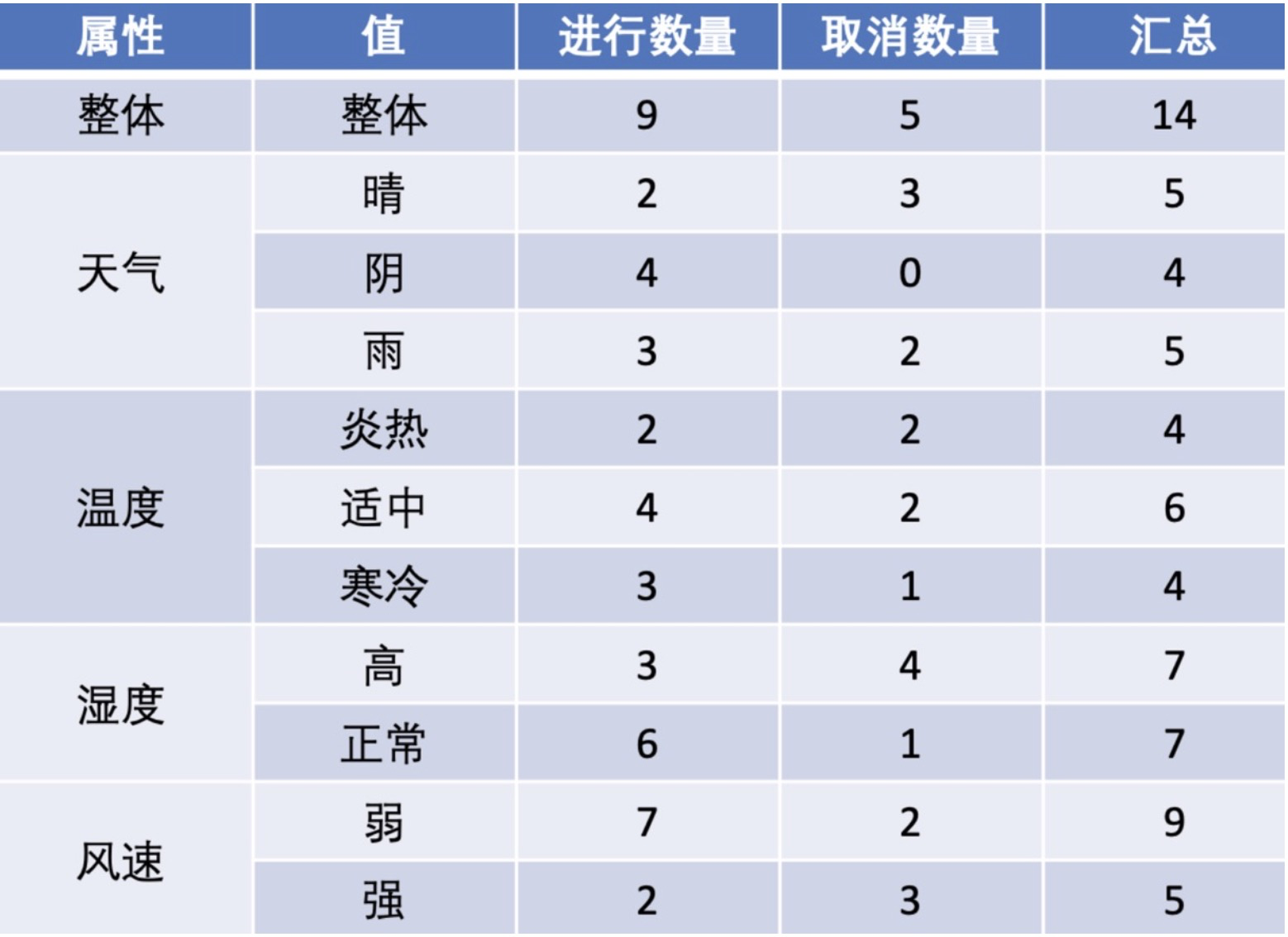
该数据集有四个属性,属性集合A={ 天气,温度,湿度,风速}, 类别标签有两个,类别集合L={进行,取消}。
a.计算类别信息熵
类别信息熵表示的是所有样本中各种类别出现的不确定性之和。根据熵的概念,熵越大,不确定性就越大,把事情搞清楚所需要的信息量就越多。
![]()
b.计算每个属性的信息熵
每个属性的信息熵相当于一种条件熵。他表示的是在某种属性的条件下,各种类别出现的不确定性之和。属性的信息熵越大,表示这个属性中拥有的样本类别越不“纯”。
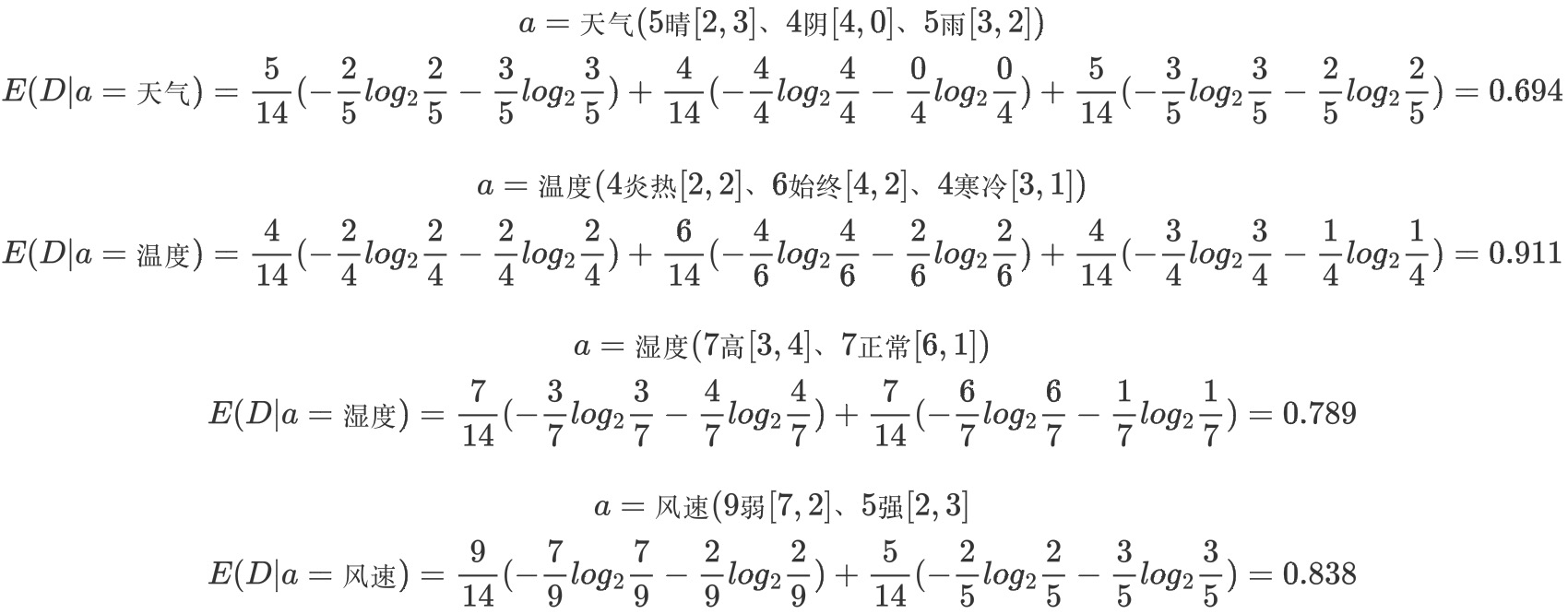
c.计算信息增益
信息增益的 = 熵 - 条件熵,在这里就是 类别信息熵 - 属性信息熵,它表示的是信息不确定性减少的程度。如果一个属性的信息增益越大,就表示用这个属性进行样本划分可以更好的减少划分后样本的不确定性,当然,选择该属性就可以更快更好地完成我们的分类目标。
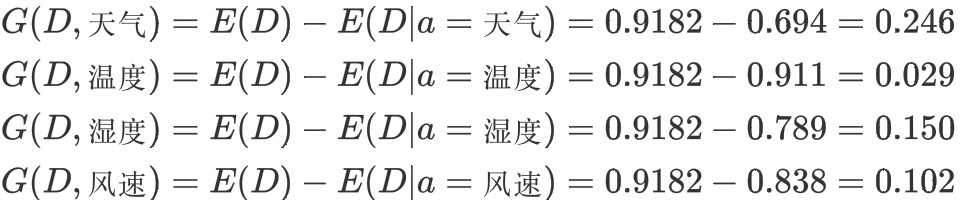
d.计算属性分裂信息度量
用分裂信息度量来考虑某种属性进行分裂时分支的数量信息和尺寸信息,我们把这些信息称为属性的内在信息(instrisic information)。信息增益率用信息增益/内在信息,会导致属性的重要性随着内在信息的增大而减小(也就是说,如果这个属性本身不确定性就很大,那我就越不倾向于选取它),这样算是对单纯用信息增益有所补偿。
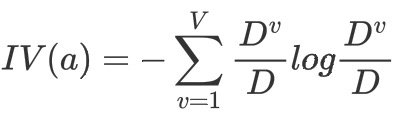
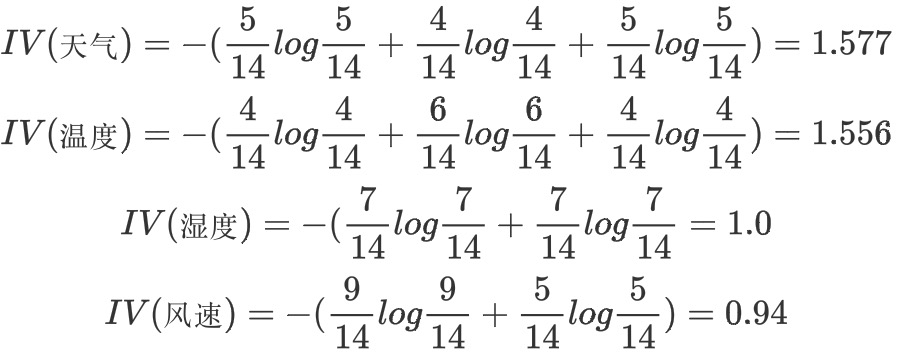
e.计算信息增益率
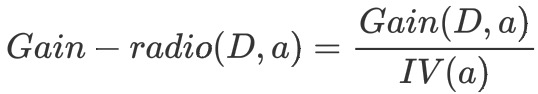

天气的信息增益率最高,选择天气为分裂属性。发现分裂了之后,天气是“阴”的条件下,类别是”纯“的,所以把它定义为叶子节点,选择不“纯”的结点继续分裂。
3.总结
3-1优点与改进
C4.5算法是用于生成决策树的一种经典算法,是ID3算法的一种延伸和优化。C4.5算法对ID3算法主要做了一下几点改进:
(1)通过信息增益率选择分裂属性,克服了ID3算法中通过信息增益倾向于选择拥有多个属性值的属性作为分裂属性的不足;
(2)能够处理离散型和连续型的属性类型,即将连续型的属性进行离散化处理;
(3)构造决策树之后进行剪枝操作;
(4)能够处理具有缺失属性值的训练数据。 C4.5算法训练的结果是一个分类模型,这个分类模型可以理解为一个决策树,分裂属性就是一个树节点,分类结果是树的结点。每个节点都有左子树和右子树,结点无左右子树。
(5)C4.5采用二分法处理连续特征,将连续特征进行排列,将连续两个值的中间值作为分裂节点,将小于该值和大于该值的样本分为两个类别,找到信息增益最大的分裂点,本质上还是用的离散特征。需注意的是,与离散属性不同,若当前节点划分属性为连续属性,该属性还可作为其后代节点的划分属性。
(6)在属性值缺失的情况下划分属性,将数据集分成两部分:没有缺失值的部分、有缺失值的部分。对每个样本设置一个权重,将没有缺失值的部分按照占据总样本的比例计算信息增益率,并乘上所占比例。
(7)给定划分属性,若样本在该属性上缺失时,若样本x在划分属性a上的取值未知,则将x同时划入所有子节点,且样本权值按所占比例和样本权值进行调整。直观地看,这就是让同一个样本以不同的概率划入到不同的子节点中。
3-2 缺点
- 信息增益率采用熵的计算,里面有大量耗时的对数计算。
- 多叉树的计算效率不如二叉树高。
- 决策树模型容易过拟合,所以应该引入剪枝策略进行处理。
Reference:
1.https://www.cnblogs.com/yuyingblogs/p/15319571.html
2.决策树(ID3、C4.5与CART)——从信息增益、信息增益率到基尼系数_戎梓漩的博客-CSDN博客_cart id3 c4.5