好难哈哈哈我依旧只做对了第一题,第二题在比赛结束后才做出来……
不过没关系每天努力一点啦~
分享一下个人做的解析,供大家参考,一起努力哇!
目录
A AcWing 4861. 构造数列
1.题目描述
2.思路分析
3.代码实现
B AcWing 4862. 浇花
1.题目描述
2.思路分析
3.代码实现
C AcWing 4863. 构造新矩阵
1.题目描述
2.思路分析
3.代码实现
4.算法知识点补充——二分模板
A AcWing 4861. 构造数列
1.题目描述

2.思路分析
本题算法:贪心
主要思路:
- 将n看成字符串,遍历其中每一个元素n[i]
- 若n[i]为0,不用管
- 若n[i]不为0,就在n[i]后面添上对应的0,并放入构造数列l中
如8009中的8,添上三个0变成8000,然后将8000放入构造数列l中
3.代码实现
T = int(input())
for _ in range(T):
n = input()
l = []
for i in range(len(n)):
if int(n[i]):
l.append(n[i] + '0' * (len(n) - (i + 1)))
print(len(l))
print(' '.join(l))B AcWing 4862. 浇花
1.题目描述
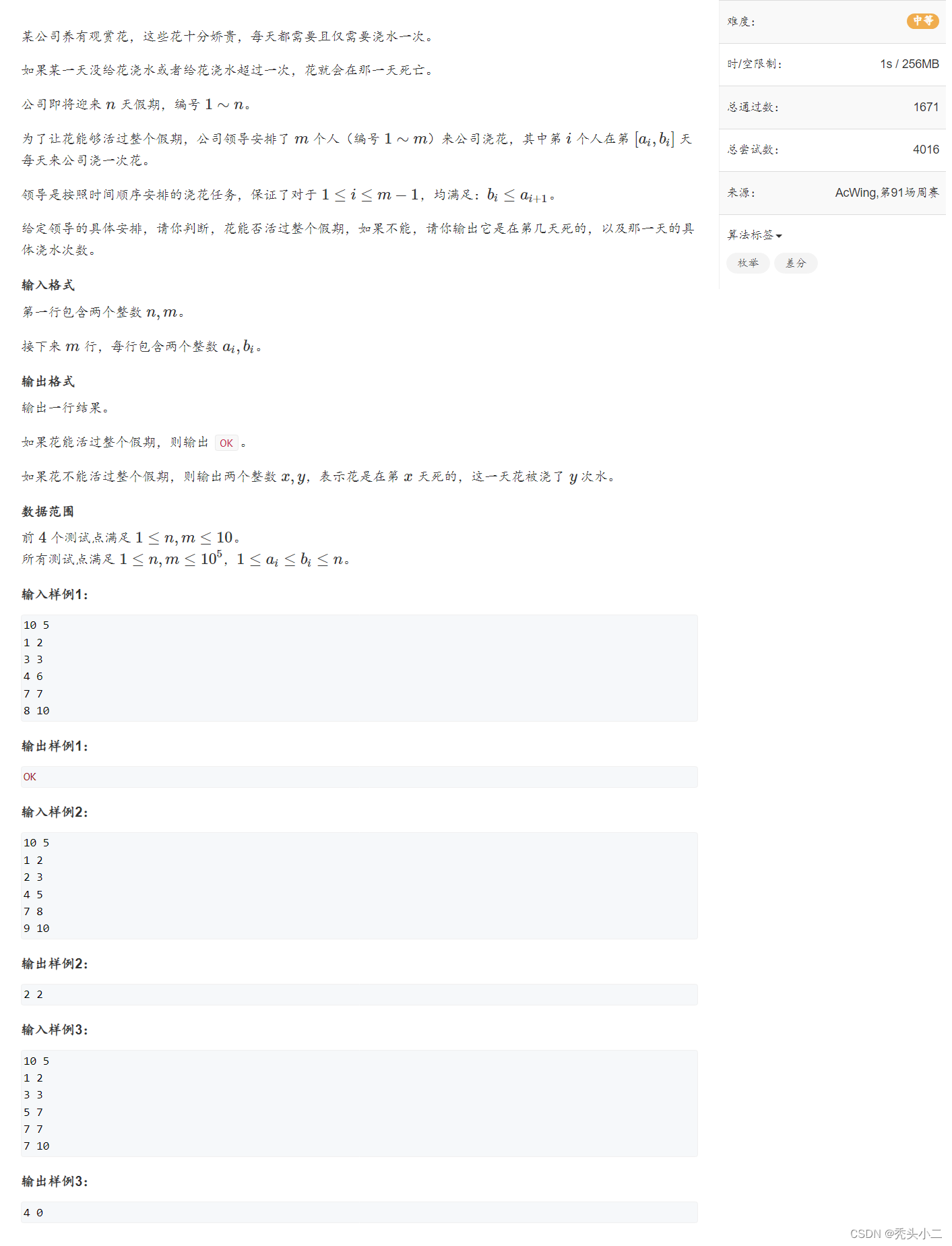
2.思路分析
本题算法:暴力(枚举)
这题我一开始琢磨了半天没理解题目,不明白[ai,bi]什么意思。
后来终于意识到这是个区间:从第ai天到第bi天。
(我是傻子……)
过程思路:
- 定义一个flag,默认为True(表示花没死)
- 遍历a[i],b[i]的元素
flag永远为True(花一直没死)的条件:
1.前一个人和后一个人浇花连续不断 ==> 遍历a[i],b[i]时一直满足b[i] + 1 == a[i + 1]
举例:前一个人在第3天浇水了,后一个人在第4天必须浇水,
如果没有在第4天浇水,第5天才浇水,花就死了。
如果后一个人还是在第3天浇水,花也死了。
所以必须满足3+1 == 4,花才不会死
2.第一个人和最后一个人必须分别在第1天和最后一天浇一次水 ==> a[1] == 1 and b[m] == n
所以我们要进行分类讨论:
- 水浇多了:
if b[i] == a[i + 1]:
flag = False
print(a[i + 1], a.count(a[i + 1]) + 1)
break如果前一个人在第3天浇水,后一个还在第3天浇水,
花就在第三天死了,因为浇了两次水。(flag = False)
如果之后的人还是在第3天浇水,那就浇了三次水,
所以我们数一下有几个在第3天浇水的人。
(至于为什么+1可以看一下下面的例子自己推敲一下哈)
'''
1 2
3 3 (i)
3 3 (i+1)
3 5
'''-
没浇水:
elif a[i + 1] - b[i] > 1:
flag = False
print(b[i] + 1, 0)
break如果前一个人在第3天浇水,后一个人在第5天浇水,(a[i + 1] - b[i] > 1)
那么第四天没人浇水,花就在第四天死了(b[i] + 1)
一旦水浇多或者没浇水,花就死了,所以不需要再遍历了,直接break跳出循环
- 水没浇多也没浇少,但是最后一天(或多天)没浇水:
if flag: if b[m] == n: print("OK") else: print(b[m] + 1, 0)(第一天不用讨论了因为我们的a,b是从0开始的,在遍历时已经判断过了)
如果最后一个人的浇水天数里没有n,说明最后一天(或多天)没浇水。
比如10天假期,最后一个人在第8天浇了水之后就不浇了,那么后两天都没浇水,
所以花在第9天(b[m] + 1)死了
ps:本题也可用差分
3.代码实现
n, m = map(int, input().split())
a, b = [0] * (m + 1), [0] * (m + 1)
for i in range(1, m + 1):
a[i], b[i] = map(int, input().split())
flag = True
for i in range(m):
if b[i] == a[i + 1]:
flag = False
print(a[i + 1], a.count(a[i + 1]) + 1)
break
elif a[i + 1] - b[i] > 1:
flag = False
print(b[i] + 1, 0)
break
if flag:
if b[m] == n:
print("OK")
else:
print(b[m] + 1, 0)C AcWing 4863. 构造新矩阵
1.题目描述
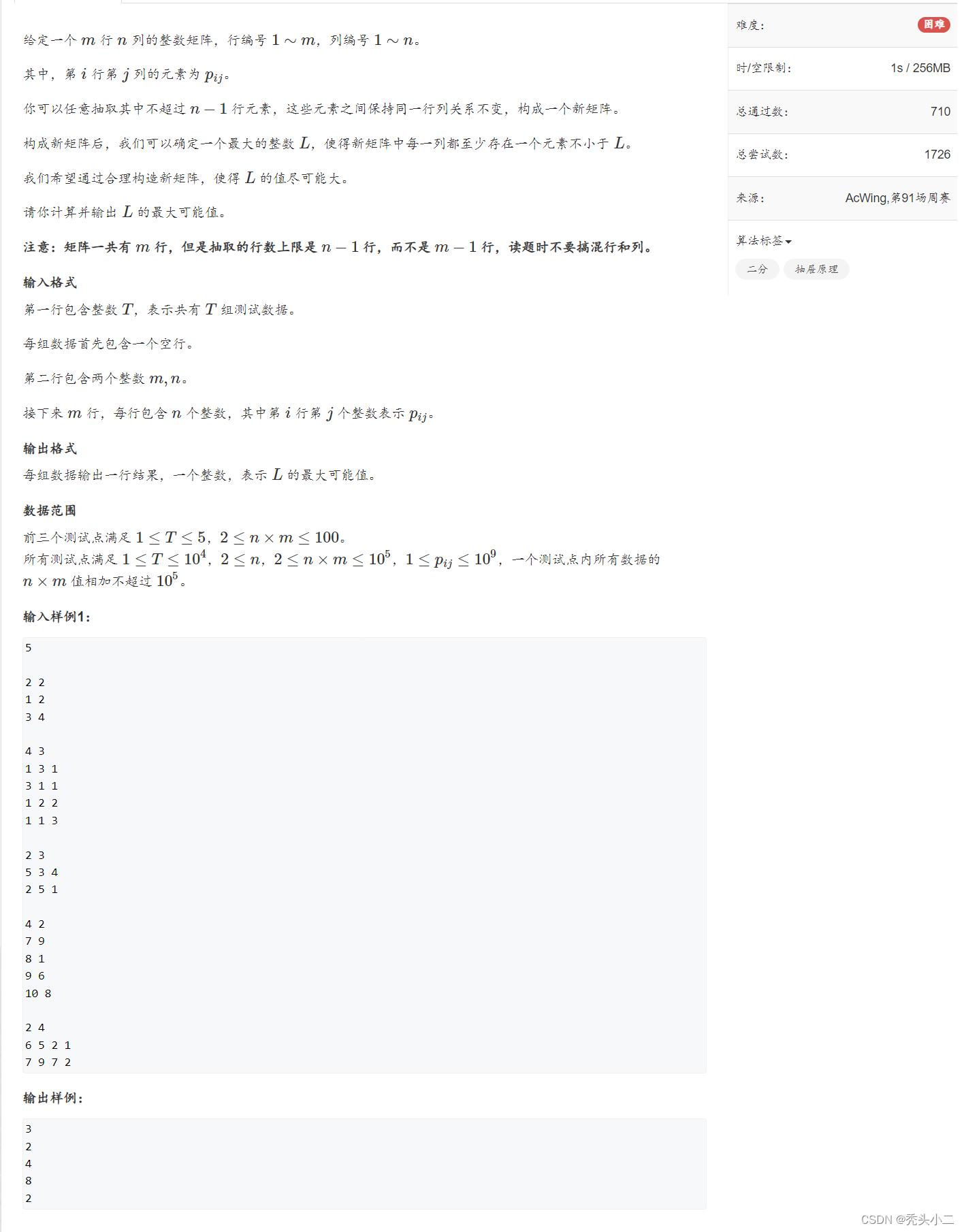
2.思路分析
本题算法:二分
过程思路:
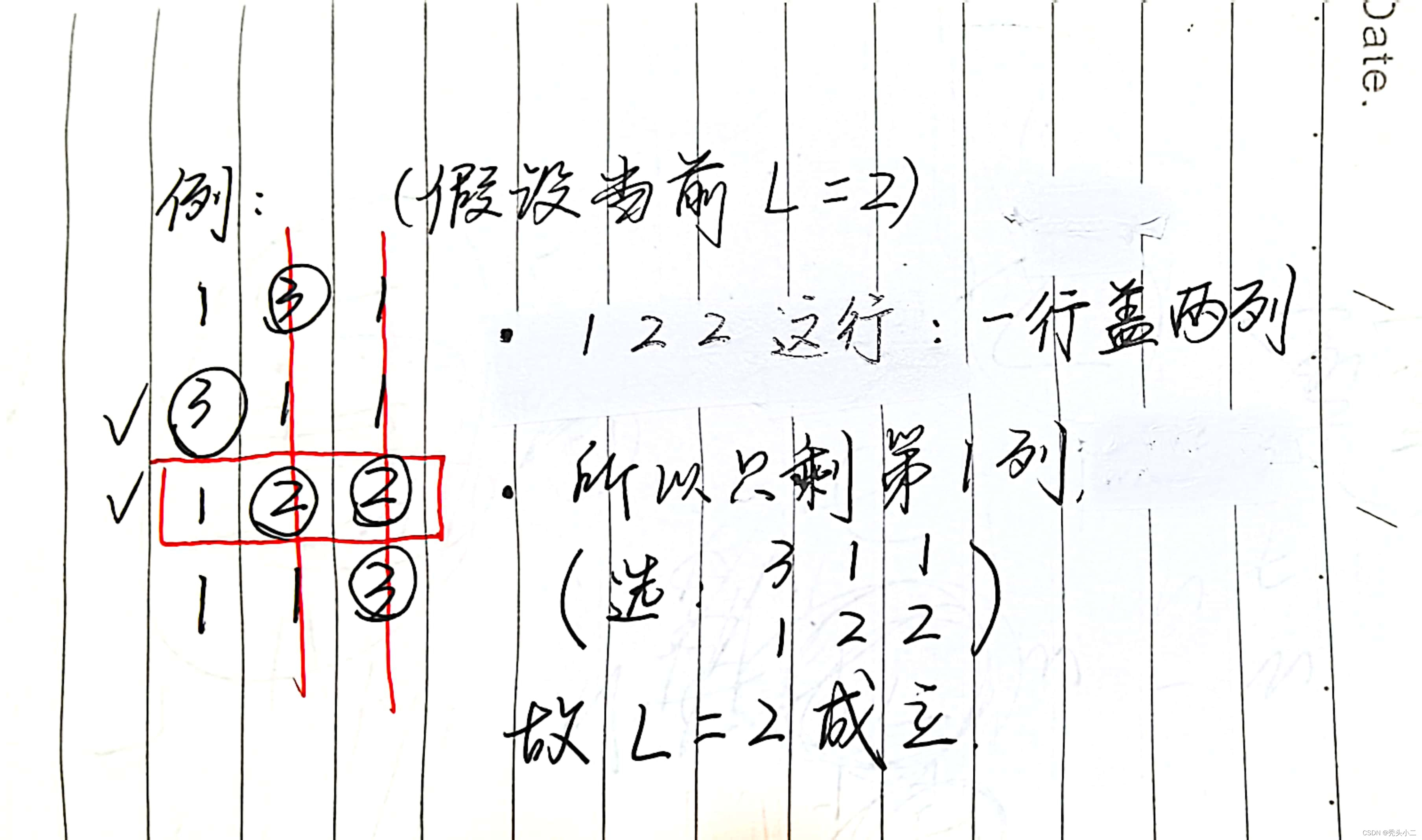
1. 构成新矩阵后,我们可以确定一个最大的整数 L,使得新矩阵中每一列都至少存在一个元素不小于 L。
将上面这句话转换为:确定一个最大的整数 L,使得新矩阵中每一列的最大值>=L
2.本题数据量非常大,所以采取二分法来优化。
3.虽然说不超过n-1行,但是我们能多选绝对不少选,所以我们把n-1行都选上,也就是把>=L的值都圈上。(因为多选了没事,即使这一行数字比较小,我们也不需要管它,我们的目光是集中在大值上的;但是少选可能会漏掉一些关键的大值)
ps:圈定义bool类型来表示
4.运用抽屉原理(也可以直接想)
当一行有2个元素都>=L(两个圈),那就选这行,因为这一行满足了两列
那么剩下的n-2列,不管我选哪一行,当前L都成立
即:
- 1行盖2列
- n-2行盖n-2列
(当然前提是:每一列都至少有一个元素>=L,否则必定不成立,此处可以另写一个判断)
3.代码实现
T = int(input())
for _ in range(T):
kong = input()
m, n = map(int, input().split())
p, max_p = [], []
for i in range(m):
p.append(list(map(int, input().split())))
max_p.append(max(p[i]))
# 二分求最优解(L最大值)
l = 1
r = max(max_p)
while l < r:
L = (l + r + 1) // 2 # 要+1,不然死循环
# 求当前L成不成立(该矩阵满不满足当前L)
flag = [[False] * n for _ in range(m)] # 默认矩阵元素都没有圈
succeed = False # 默认不成立
# 将>=L的元素都圈上
for i in range(m):
for j in range(n):
if p[i][j] >= L:
flag[i][j] = True
# 如果这一行有两个及以上的元素被圈上了,当前L可能成立
if flag[i].count(True) >= 2:
succeed = True
# 如果一列上没有一个圈,必不成立
for i in range(n):
lie = [] # 每一列
for j in range(m):
lie.append(flag[j][i])
if lie.count(True) == 0:
succeed = False
break
if succeed:
l = L # 成立的,所以不+1,万一此时就是最优解,加了个1就没了
else:
r = L - 1 # 当前L不成立
print(r)4.算法知识点补充——二分模板
模板一:
while l < r:
mid = l + r >> 1 # (l + r) // 2
if check(mid): # check()判断mid是否成立
r = mid
else:
l = mid + 1模板二:
while l < r:
mid = l + r + 1 >> 1
if check(mid):
l = mid
else:
r = mid - 1细节处(很关键):
只要是往左找答案,就用第一个模板,mid不用加一,r=mid,l加一;
只要是往右找答案,就用第二个模板,mid要加一,l=mid,r要减一;
这里的细节要着重理解记忆!!!
本题是往右找答案,mid+1是防止死循环,l不加1是防止错过正确答案
此处模板参考:二分查找 & 二分答案 万字详解,超多例题,带你学透二分。_小酒窝.的博客-CSDN博客_二分查找题目
感谢大佬~
最后一题分析参考y总的哈,大家也可以直接看y总的讲解。
如有帮助可以点赞收藏嘛~
如有不足或不解之处欢迎评论留言~