专栏：神经网络复现目录

深度学习神经网络基础知识(二)

本文讲述神经网络基础知识，具体细节讲述前向传播，反向传播和计算图，同时讲解神经网络优化方法：权重衰减，Dropout等方法，最后进行Kaggle实战，具体用一个预测房价的例子使用上述方法。

文章部分文字和代码来自《动手学深度学习》

文章目录

深度学习神经网络基础知识(二)
- 范数
- 权重衰减
- - 定义
  - 权重衰减的从零实现
  - 运行结果
  - 权重衰减的简洁实现
- 暂退法（Dropout）
- - 定义
  - 暂退法的从零实现
  - 运行结果
  - 暂退法的简洁实现

范数

$L_p$ 范数是一种向量范数，定义如下：

$\left|\boldsymbol{x}\right|{p}=\left(\left|x{1}\right|^{p}+\left|x_{2}\right|^{p}+\cdots+\left|x_{n}\right|^{p}\right)^{\frac{1}{p}}$

其中， $\geq 1$ ， $\boldsymbol{x}=(x_1, x_2, \cdots, x_n)$ 是一个 $n$ 维向量。当 $p = 2$ 时， $L_p$ 范数也称为欧几里得范数（Euclidean norm），常用于表达向量的长度或者大小。当 $p = 1$ 时， $L_p$ 范数也称为曼哈顿范数（Manhattan norm）或者 $\ell_1$ 范数，常用于表达向量中各个元素的绝对值之和。当 $\rightarrow \infty$ 时， $L_p$ 范数也称为切比雪夫范数（Chebyshev norm）或者 $\ell_\infty$ 范数，常用于表达向量中绝对值最大的元素。

$L_0$ 范数不是向量范数，因为它并不满足向量范数的三个条件之一，即正定性。通常把向量 $\boldsymbol{x}$ 中非零元素的个数称为 $\boldsymbol{x}$ 的 $L_0$ 范数，但这并不是一个数学上合理的定义。

常见的范数有以下几种：

$L^1$ 范数： $\sum{i=1}^n |x_i|$

$L^2$ 范数： $\sqrt{\sum{i=1}^n x_i^2}$

权重衰减

定义

权重衰减是一种用于降低过拟合的正则化技术。其原理是通过在模型训练过程中增加一个惩罚项（也称作正则化项），来抑制模型的复杂度，从而达到减小过拟合的效果。

具体来说，在损失函数中添加一个正则化项，一般会对模型的参数进行 $L_2$ 范数的约束，也就是让模型的参数尽量小。这样，在模型训练过程中，不仅会尽量减小训练数据的损失，还会尽量让模型参数的平方和小，从而达到抑制模型过拟合的效果。

权重衰减的损失函数为：
在这里插入图片描述
其中 $\mathcal{L}(\boldsymbol{w}, b)$ 是原始的无正则化项的损失函数， $|\boldsymbol{w}|^2$ 表示模型参数的 $L_2$ 范数， $\lambda$ 是正则化强度， $n$ 是训练样本数。

在优化算法中，我们需要对这个损失函数进行梯度下降。由于正则化项的梯度为 $\frac{\lambda}{n}\boldsymbol{w}$ ，因此我们需要对原始的梯度加上这个正则化项的梯度：

$\leftarrow (1 - \frac{\eta \lambda}{|B|})w - \frac{\eta}{|B|} \sum_{i \in B} \frac{\partial}{\partial w} l^{(i)}(w, b)$

其中， $w$ 是待更新的权重参数， $\eta$ 是学习率， $\lambda$ 是正则化超参数（即权重衰减超参数）， $∣ B ∣$ 是当前小批量中的样本数， $l^{(i)}(w, b)$ 是第 $i$ 个样本的损失函数， $\frac{\partial}{\partial w} l^{(i)}(w, b)$ 是对权重参数的损失函数梯度。

权重衰减的从零实现

构造生成数据集的函数

%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2l
#生成数据集
def synthetic_data(w,b,num):
    #x通过正态分布生成
    x=torch.normal(0,1,(num,len(w)))
    y=torch.matmul(x,w)+b
    #数据集中加入噪声
    y+=torch.normal(0,0.01,y.shape)
    return x,y.reshape(-1,1)

构造一个数据迭代器

def load_array(data_arrays, batch_size, is_train=True):  #@save
    """构造一个PyTorch数据迭代器"""
    dataset = data.TensorDataset(*data_arrays)
    return data.DataLoader(dataset, batch_size, shuffle=is_train)

生成数据集

n_train, n_test, num_inputs, batch_size = 20, 100, 200, 5
true_w, true_b = torch.ones((num_inputs, 1)) * 0.01, 0.05
train_data = synthetic_data(true_w, true_b, n_train)
train_iter = load_array(train_data, batch_size)
test_data = synthetic_data(true_w, true_b, n_test)
test_iter = load_array(test_data, batch_size, is_train=False)

初始化模型参数

def init_params():
    w = torch.normal(0, 1, size=(num_inputs, 1), requires_grad=True)
    b = torch.zeros(1, requires_grad=True)
    return [w, b]

定义L2范数惩罚

def l2_penalty(w):
    return torch.sum(w.pow(2)) / 2

训练

def train(lambd):
    w, b = init_params()
    net, loss = lambda X: d2l.linreg(X, w, b), d2l.squared_loss
    num_epochs, lr = 100, 0.003
    animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
                            xlim=[5, num_epochs], legend=['train', 'test'])
    for epoch in range(num_epochs):
        for X, y in train_iter:
            # 增加了L2范数惩罚项，
            # 广播机制使l2_penalty(w)成为一个长度为batch_size的向量
            l = loss(net(X), y) + lambd * l2_penalty(w)
            l.sum().backward()
            d2l.sgd([w, b], lr, batch_size)
        if (epoch + 1) % 5 == 0:
            animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),
                                     d2l.evaluate_loss(net, test_iter, loss)))
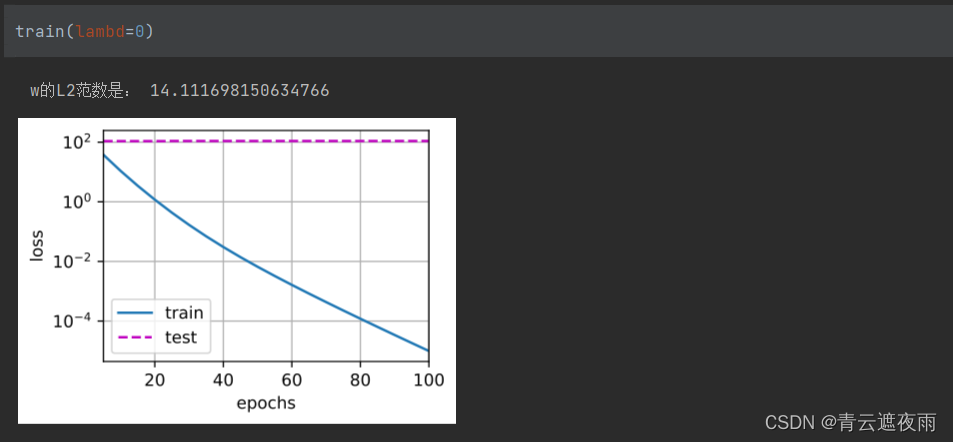
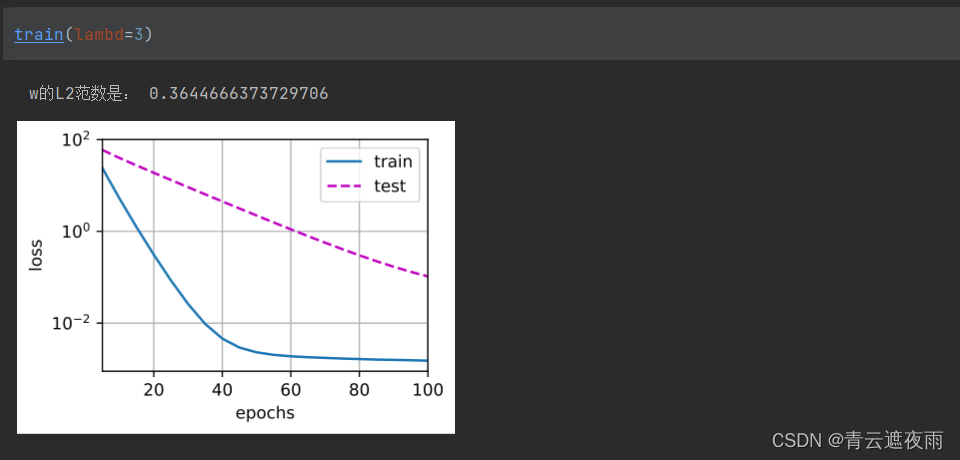
    print('w的L2范数是：', torch.norm(w).item())

运行结果

未使用权重衰减
在这里插入图片描述
使用权重衰减

权重衰减的简洁实现

def train_concise(weight_decay):
    net = nn.Sequential(nn.Linear(num_inputs, 1))
    for param in net.parameters():
        param.data.normal_()
    loss = nn.MSELoss(reduction='none')
    num_epochs, lr = 100, 0.003
    # 偏置参数没有衰减
    trainer  = optim.SGD(model.parameters(), lr=lr, weight_decay=weight_decay)
    animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
                            xlim=[5, num_epochs], legend=['train', 'test'])
    for epoch in range(num_epochs):
        for X, y in train_iter:
            trainer.zero_grad()
            l = loss(net(X), y)
            l.mean().backward()
            trainer.step()
        if (epoch + 1) % 5 == 0:
            animator.add(epoch + 1,
                         (d2l.evaluate_loss(net, train_iter, loss),
                          d2l.evaluate_loss(net, test_iter, loss)))
    print('w的L2范数：', net[0].weight.norm().item())

关注这行代码

trainer  = optim.SGD(model.parameters(), lr=lr, weight_decay=weight_decay)

其中weight_decay参数即为lambda

暂退法（Dropout）

定义

Dropout是一种用于神经网络的正则化技术，旨在减少模型的过拟合。该算法的核心思想是在网络的训练过程中随机“丢弃”一部分神经元，从而强制模型学习更加鲁棒和通用的特征。在测试时，所有神经元都保留，但是输出值需要乘以一个固定比例以保持期望输出不变。

具体来说，假设我们有一个包含 $L$ 个层的神经网络。对于第 $i$ 层，它的输出为 $h^{(i)}$ 。在训练时，我们按照一定的概率 $p$ 来随机选择一部分神经元，将它们的输出值设置为0。因此，第 $i$ 层的输出为：

$\tilde{h}^{(i)}=r^{(i)}\odot h^{(i)}$

其中 $r^{(i)}$ 是一个与 $h^{(i)}$ 具有相同形状的二进制向量，其中元素值为1的概率为 $p$ ，值为0的概率为 $1 - p$ ， $\odot$ 表示按元素相乘。在前向传播过程中，我们使用 $\tilde{h}^{(i)}$ 代替 $h^{(i)}$ 进行计算。在反向传播过程中，由于某些神经元的输出被设置为0，我们只需要将其对应的梯度清零即可。

在测试时，我们需要保留所有神经元的输出，但是为了保持期望输出不变，我们需要将所有神经元的输出值乘以 $p$ ，即：

$h^{(i)}_{test}=p\cdot h^{(i)}$

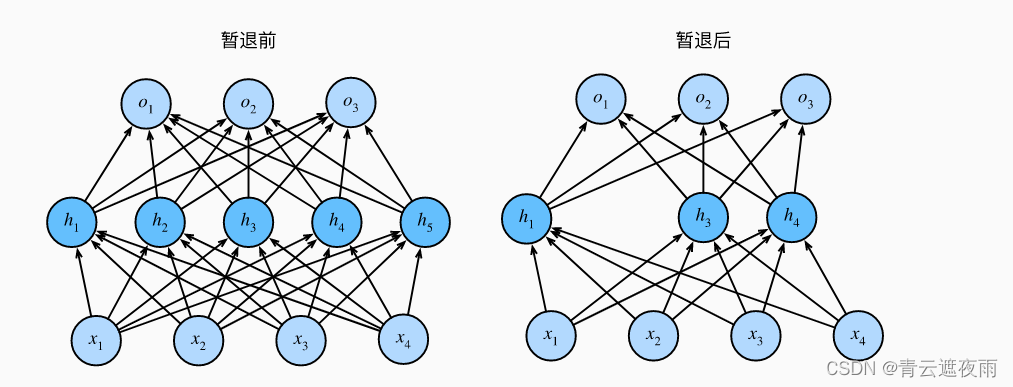
下图形象的展示了暂退法的效果：
在这里插入图片描述

暂退法的从零实现

这是一个实现dropout算法的函数，它接受一个输入张量X和一个dropout概率dropout，然后返回一个应用了dropout的输出张量。

具体来说，该函数会生成一个与X形状相同的掩码张量，其中每个元素都是随机生成的0或1，生成方式是根据概率dropout与0比较，如果大于dropout则为1，否则为0。然后将掩码张量与X相乘并除以(1 - dropout)，这个操作相当于将保留下来的元素值除以它们的概率。最后返回应用了dropout的输出张量。

import torch
from torch import nn
from d2l import torch as d2l


def dropout_layer(X, dropout):
    assert 0 <= dropout <= 1
    # 在本情况中，所有元素都被丢弃
    if dropout == 1:
        return torch.zeros_like(X)
    # 在本情况中，所有元素都被保留
    if dropout == 0:
        return X
    mask = (torch.rand(X.shape) > dropout).float()
    return mask * X / (1.0 - dropout)

具体关注一下：

mask = (torch.rand(X.shape) > dropout).float()

这一行代码的作用是生成一个与X形状相同的张量mask，并且其中的每个元素都是0或1。这里的0和1表示相应的X元素是否被保留，而生成这些0和1的方式是随机的，因为我们用torch.rand()函数生成一个形状与X相同的随机张量，并将其中的每个元素与dropout做比较。

比较的结果是一个布尔类型的张量，即对于X中的每个元素，如果随机生成的相应元素的值大于dropout，那么在mask中相应位置的值为1，表示保留；反之，如果随机生成的值小于等于dropout，那么在mask中相应位置的值为0，表示丢弃。

最后，为了保持期望的值不变，我们将所有保留的元素的值除以 1- dropout，这是因为被保留的概率是1- dropout。所以，最终得到的输出是一个X的掩码版本，其中的一些元素被随机置为零。

测试一下我们写的dropout层

X= torch.arange(16, dtype = torch.float32).reshape((2, 8))
print(X)
print(dropout_layer(X, 0.))
print(dropout_layer(X, 0.5))
print(dropout_layer(X, 1.))

定义模型参数

num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256

定义模型
这次我们使用了和以往不同、面向对象的模型定义方式，需要重写__init__和forward函数

init 方法用于定义网络结构，包括网络层、激活函数、损失函数等，并初始化权重、偏差等参数。这些网络参数在训练过程中会不断地更新。

forward 方法用于定义数据在网络中的正向传播（也就是模型从输入到输出的计算过程），即输入数据经过网络的各层计算，最终得到输出。在该方法中，我们可以任意组合各种网络层及其参数，实现自己所需要的网络结构和计算过程。

在下面的代码中，Net 类继承自 nn.Module，其中 init 方法用于定义网络的结构，包括三个全连接层和一个 ReLU 激活函数。forward 方法用于实现数据在网络中的正向传播计算，包括将输入 X 经过全连接层和激活函数得到输出 out。在训练模式中，还会在第一个全连接层和第二个全连接层后面添加 dropout 层。

dropout1, dropout2 = 0.2, 0.5

class Net(nn.Module):
    def __init__(self, num_inputs, num_outputs, num_hiddens1, num_hiddens2,
                 is_training = True):
        super(Net, self).__init__()
        self.num_inputs = num_inputs
        self.training = is_training
        self.lin1 = nn.Linear(num_inputs, num_hiddens1)
        self.lin2 = nn.Linear(num_hiddens1, num_hiddens2)
        self.lin3 = nn.Linear(num_hiddens2, num_outputs)
        self.relu = nn.ReLU()

    def forward(self, X):
        H1 = self.relu(self.lin1(X.reshape((-1, self.num_inputs))))
        # 只有在训练模型时才使用dropout
        if self.training == True:
            # 在第一个全连接层之后添加一个dropout层
            H1 = dropout_layer(H1, dropout1)
        H2 = self.relu(self.lin2(H1))
        if self.training == True:
            # 在第二个全连接层之后添加一个dropout层
            H2 = dropout_layer(H2, dropout2)
        out = self.lin3(H2)
        return out


net = Net(num_inputs, num_outputs, num_hiddens1, num_hiddens2)

训练和测试

num_epochs, lr, batch_size = 10, 0.5, 256
loss = nn.CrossEntropyLoss(reduction='none')
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
trainer = torch.optim.SGD(net.parameters(), lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

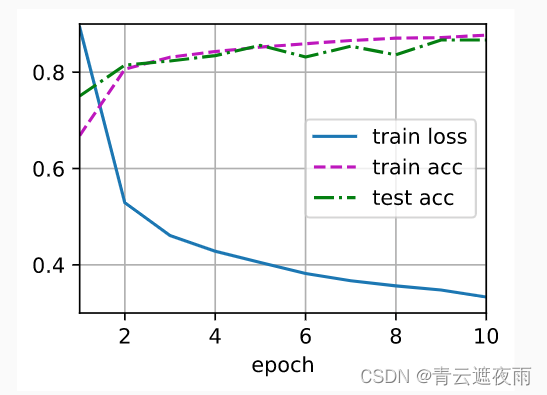
运行结果

在这里插入图片描述

暂退法的简洁实现

net = nn.Sequential(nn.Flatten(),
        nn.Linear(784, 256),
        nn.ReLU(),
        # 在第一个全连接层之后添加一个dropout层
        nn.Dropout(dropout1),
        nn.Linear(256, 256),
        nn.ReLU(),
        # 在第二个全连接层之后添加一个dropout层
        nn.Dropout(dropout2),
        nn.Linear(256, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);

或者是

class Net(nn.Module):
    def __init__(self, input_size, hidden_size, output_size, dropout_prob):
        super(Net, self).__init__()
        self.fc1 = nn.Linear(input_size, hidden_size)
        self.fc2 = nn.Linear(hidden_size, hidden_size)
        self.fc3 = nn.Linear(hidden_size, output_size)
        self.dropout = nn.Dropout(p=dropout_prob)

    def forward(self, x):
        x = torch.relu(self.fc1(x))
        x = self.dropout(x)
        x = torch.relu(self.fc2(x))
        x = self.dropout(x)
        x = self.fc3(x)
        return x