写在前面：

军训好累......

题目：剑指 Offer 11. 旋转数组的最小数字 - 力扣（Leetcode）

题目的接口：

class Solution {
public:
    int minArray(vector<int>& numbers) {

    }
};

解题思路1：

看到这个题目，我第一个想到的就是，

直接遍历数组，然后找出最小之就行，

用O(N)算法暴力解决。

代码：

class Solution {
public:
    int minArray(vector<int>& numbers) {
        //将Min初始化成一个很大的数
        int Min = INT_MAX;

        //遍历数组
        for(int i = 0;i<numbers.size();i++)
        {
            //找出最小值
            Min = min(Min, numbers[i]);
        }
        return Min;
    }
};

过啦！！！

如果只是这样的话，那这题刷的可没什么质量，

如果以后面试的时候，面试官问你怎么提高这个算法的效率，你该怎么办？

所以，我决定在写个二分来做这道题，将算法时间优化成O(logN)。

解题思路2：

因为这是原来是一个升序数组，

如果我们将旋转数组中的旋转的第一个值作为旋转点，

而旋转点就是这个数组的最小值，

所以我们直接找旋转点就行。

用二分的思想，设置 l、r 作为左右下标，取中间 mid 为中间下标。

如果numbers[mid] > numbers[r]，旋转点一定在右边区间[ m + 1，j ]。

如果numbers[mid] < numbers[r]，旋转点一定在左边区间[ l，m ]。

如果numbers[mid] = numbers[r]，特殊情况就让 r--。

当 l = r 的时候，返回numbers[l]就是旋转点。

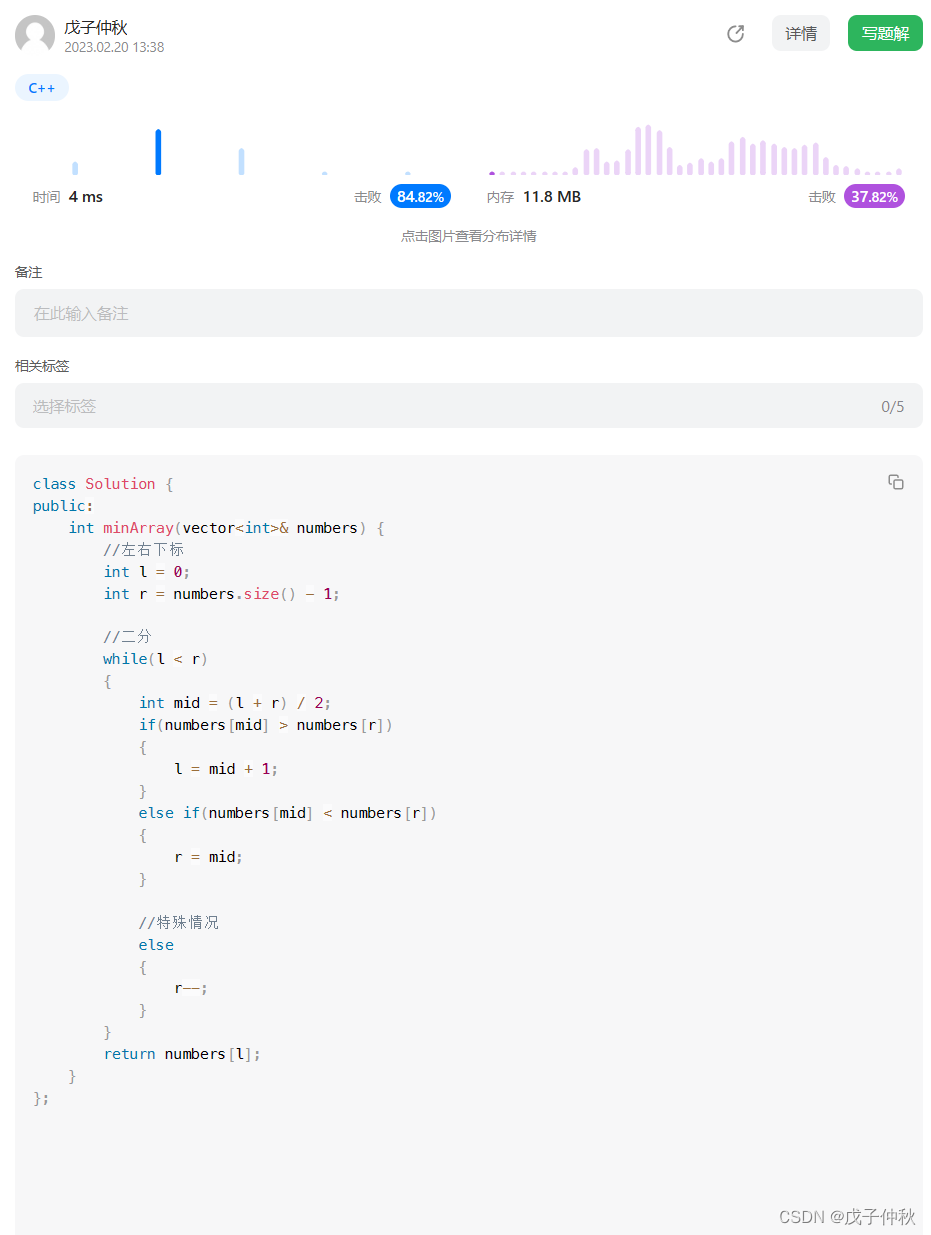
代码：

class Solution {
public:
    int minArray(vector<int>& numbers) {
        //左右下标
        int l = 0;
        int r = numbers.size() - 1;

        //二分
        while(l < r)
        {
            int mid = (l + r) / 2;
            if(numbers[mid] > numbers[r])
            {
                l = mid + 1;
            }
            else if(numbers[mid] < numbers[r])
            {
                r = mid;
            }
            
            //特殊情况
            else
            {
                r--;
            }
        }
        return numbers[l];
    }
};

但其实这种方法也有缺陷，

他的时间复杂度还是O(N)，只是优化了大部分的情况，

在遇到特殊情况的时候（也就是numbers[mid] = numbers[r]的时候就会退化成O(N)算法）

只是平均时间复杂度为O(logN)。