【C++修炼之路】20.手撕红黑树

news2024/9/21 5:42:30

在这里插入图片描述
每一个不曾起舞的日子都是对生命的辜负

红黑树实现:RBTree

  • 前言
  • 一.红黑树的概念及性质
    • 1.1 红黑树的概念
    • 1.2 红黑树的性质
  • 二.红黑树的结构
    • 2.1 红黑树节点的定义
    • 2.2 红黑树类的封装
  • 三.红黑树的插入
    • 情况1：只变色
    • 情况2：变色+单旋
    • 情况3：双旋
    • 插入的代码实现：
  • 四.红黑树的验证
  • 五.红黑树实现代码（完整）
    • RBTree.h
    • Test.cpp
  • 六.红黑树与AVL树的比较

前言

在上一节中我们学到了AVL树的结构及其相关性质，对于平衡树来说，AVL无疑是最完美的结构，但实际上AVL树由于完美的结构因此也要花费一定的代价，由于AVL树的结构很敏感，查找虽然最快，但插入节点后一旦偏离AVL结构就会进行旋转，而旋转就会花费一定的性能。因此我们提到的map和set的底层为了防止这种性能上的缺失，即便AVL是非常完美的结构，也不采用AVL。而是采用我们这节所要描述的红黑树。

一.红黑树的概念及性质

1.1 红黑树的概念

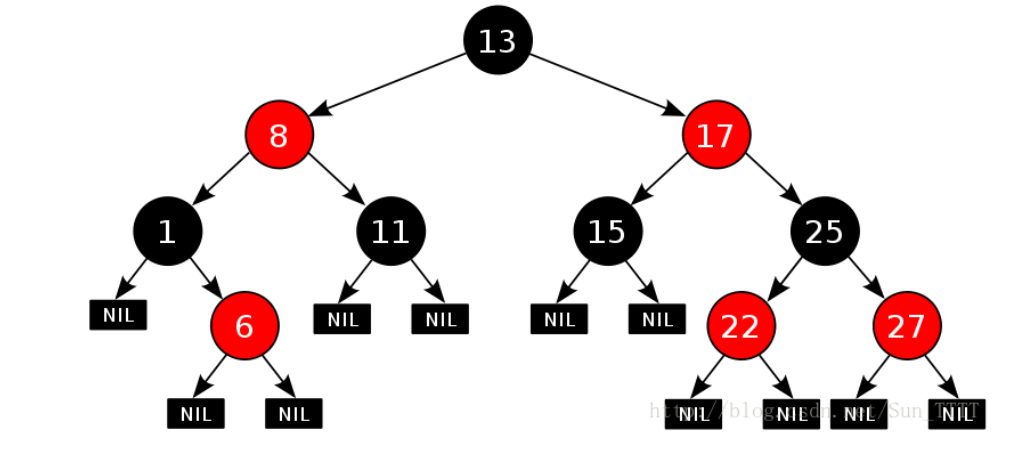
红黑树，是一种二叉搜索树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出俩倍，因而是接近平衡的。

可见红黑树的这种结构，虽然在不满足条件时会发生旋转，但敏感程度相比AVl树大大降低。

image-20230215124244019

1.2 红黑树的性质

  1. 每个结点不是红色就是黑色
  2. 根节点是黑色的
  3. 如果一个节点是红色的，则它的两个孩子结点是黑色的
  4. 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点
  5. 每个叶子结点都是黑色的（此处的叶子结点指的是空结点）

需要注意的是：对于性质3，意思就是没有连续的红色结点。

思考： 为什么满足上面的性质，红黑树就能保证：其最长路径中节点个数不会超过最短路径节点个数的两倍？

就上面的这颗红黑树来说，有11条路径（需算到空）我们只观察黑色结点，发现是接近满二叉树的。对于红黑树的最短路径，最短的极限情况就是一条路径全是黑色的结点，因为其他路径也会有相同数目的黑节点加上一定数量的红色结点，而最长路径就是一黑一红相间的路径。可见，最长的结点个数是最短结点个数的二倍。

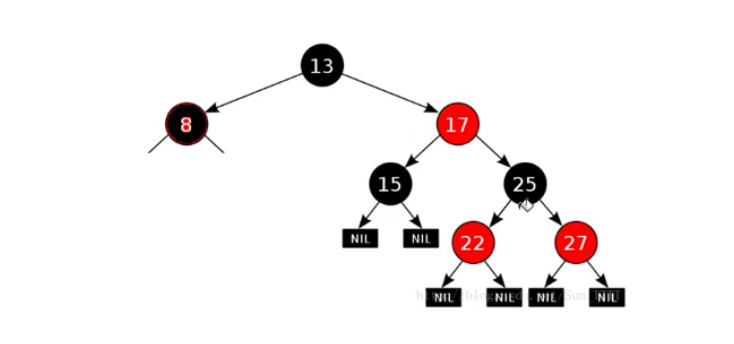
image-20230215125646671

这样就是红黑树的结构，且存在最长和最短的情况，最短为最长的二分之一。

由于红黑树确保没有一条路径会比其他路径长出俩倍，因此可以看成近似平衡，对于这种不确定的结构，自然就有最好的情况和最坏的情况。

  • 最好情况：（左右平衡）

全黑或者每条路径都是一黑一红相间的路径，接近满二叉树。那么此时设全黑的路径长度为h结点数量为N，则2^h - 1 + _ = N（_代表红色结点，由于一条路径红色结点数量一定小于等于黑色，所以可以忽略计算）此时，h = logN。

  • 最坏情况：（左右极其不平衡）

左子树全黑，且右子树一黑一红。那么此时最长路径为2*logN。

总结： 可以看出，在对数的加持下，即便是最坏情况，对于计算机来说相差也不是很大。虽不如AVL的极度平衡，但红黑树明显在插入节点时显得张弛有力。对于AVL来说，说是过刚易折也不为过，往往像红黑树那样增加一定的柔韧性，才是最后的选择。

二.红黑树的结构

2.1 红黑树节点的定义

相比较AVL树，红黑树的结点仍是三叉链这个结构，为后续不满足结构的条件旋转做准备。此外，和AVL树结点不同的是，红黑树不再有平衡因子这一变量，而是多了一个定义颜色的变量，颜色变量通过枚举实现。下面看看结点定义的代码：

enum Color//颜色采用枚举，但STL库采用的是特殊的bool值，后续会看
{
	RED,//0
	BLACK,//1
};

template<class K, class V>
struct RBTreeNode
{
	pair<K, V> _kv;
	RBTreeNode<K, V>* _left;
	RBTreeNode<K, V>* _right;
	RBTreeNode<K, V>* _parent;
	Color _col;

	RBTreeNode(const pair<K, V>& kv)
		:_kv(kv)
		,_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_col(RED)//默认哪种颜色都可以，因为后续会改
	{}

};

2.2 红黑树类的封装

enum Color//颜色采用枚举，但STL库采用的是特殊的bool值，后续会看
{
	RED,//0
	BLACK,//1
};

template<class K, class V>
struct RBTreeNode
{
	pair<K, V> _kv;
	RBTreeNode<K, V>* _left;
	RBTreeNode<K, V>* _right;
	RBTreeNode<K, V>* _parent;
	Color _col;

	RBTreeNode(const pair<K, V>& kv)
		:_kv(kv)
		,_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_col(RED)//默认哪种颜色都可以，因为后续会改
	{}

};

template<class K, class V>
class RBTree
{
	typedef RBTreeNode<K, V> Node;
public:
    //成员函数
    bool Insert(const pair<K, V>& kv)
    {
        
    }
private:
	Node* _root = nullptr;
};

三.红黑树的插入

与AVL树一样，在插入中需要考虑的因素众多，但相比AVL，红黑树在插入时的情况少很多，因为其结构没有AVL树的高度平衡。

在红黑树的性质中，第三，第四条尤为重要。即：

  • 如果一个节点是红色的，则它的两个孩子结点是黑色的
  • 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点

如果我们新插入的结点的颜色为黑的话，插入之后一定会打破上述第二个结构，导致每条路径的黑结点数量不同；如果新插入的节点的颜色为红色的话，也有可能不满足情况，如果插入节点的父节点为黑的话还好，但如果父节点为红，也就不满足这个条件了。因此，插入节点的颜色尤为重要，经过上述考虑，插入节点的颜色为红无疑是最好的选择，因为有可能满足条件，有可能不满足条件，但插入黑色一定不满足。如果插入红色的也不满足，那就后期处理就好了。

  • 插入节点的颜色必须为红

检测新节点插入后，红黑树的性质是否造到破坏
因为新节点的默认颜色是红色，因此：如果其双亲节点的颜色是黑色，没有违反红黑树任何性质，则不需要调整；但当新插入节点的双亲节点颜色为红色时，就违反了性质三不能有连在一起的红色节点，此时需要对红黑树分情况来讨论：
约定: cur为当前（插入）节点，p为父节点，g为祖父节点，u为叔叔节点

对于新节点的插入，与父节点和父节点的兄弟节点也有关，下面就看看各种情况：

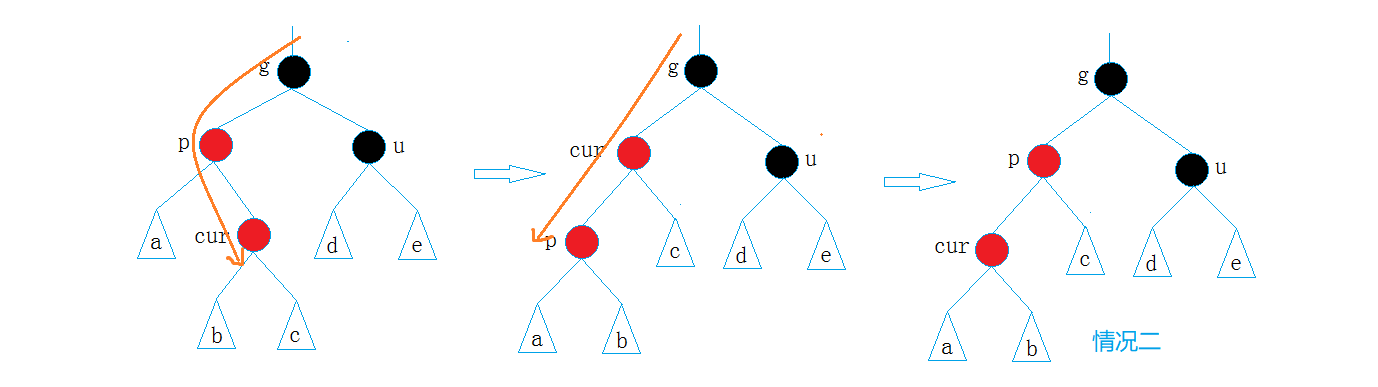
情况1：只变色

  • cur为红，p为红，g为黑，u存在且为红

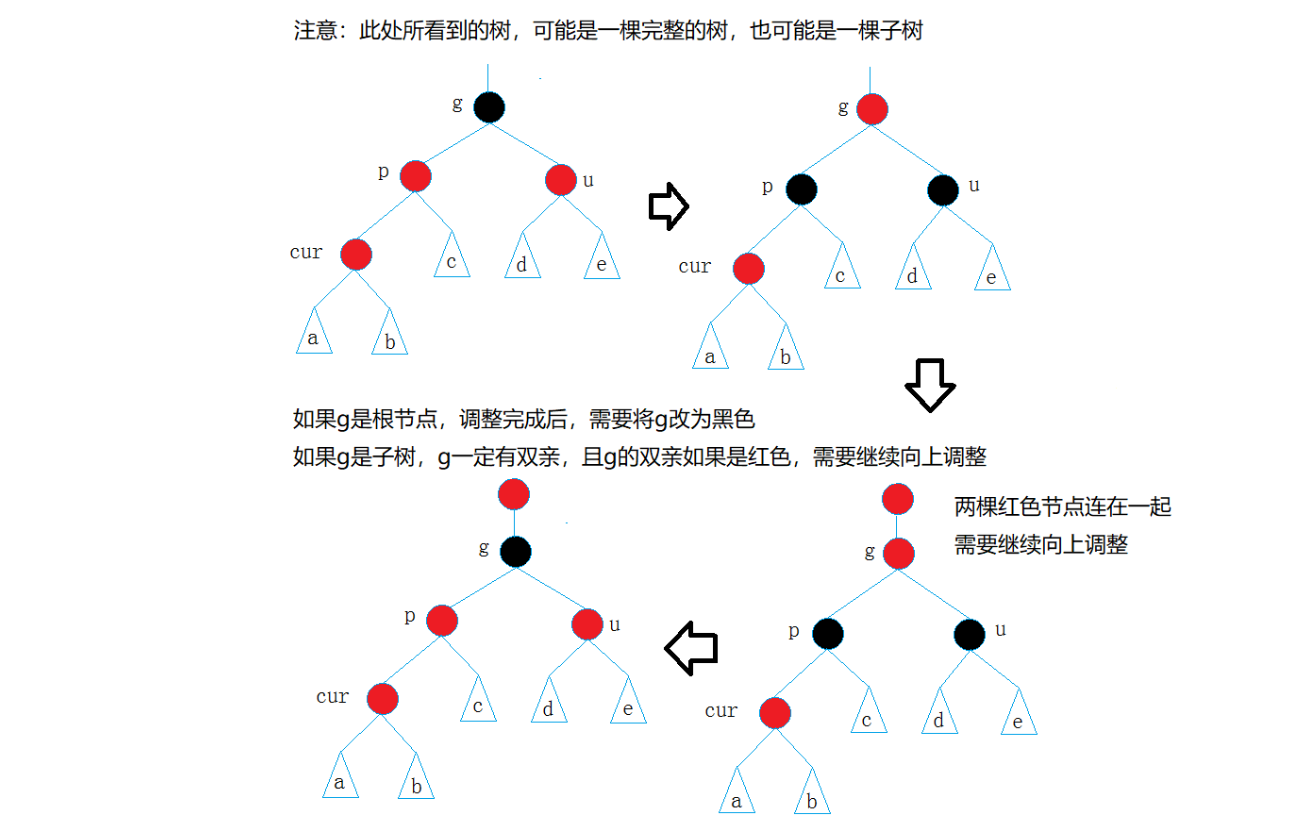
image-20230215145901714

通过上面图的步骤，我们大致知道了思路，如果红色结点连续，为了满足红黑树的不能有连续红色结点的性质，我们需要将其双亲也就是父亲结点变成黑色，如果这棵树是子树，那么为了保证黑色结点数量不变，我们需要将g变红，如果g的双亲仍是红色，那么就一直往上更新迭代。对于上图，实际上同样是个抽象图，因为a,b,c,d,e可以使任意的红黑树子树，情况也会随着这几个抽象树节点的增加而变化的非常多，因此我们只需要牢记这种抽象图即可。

cur和p均为红，违反了性质三，此处能否将p直接改为黑？
解决方式：将p,u改为黑，g改为红，然后把g当成cur，继续向上调整。

可以看出，红色结点的增加是因为插入节点，黑色节点的增加是为了保证红黑树结构的性质从红色结点变化而来的。

情况2：变色+单旋

  • cur为红，p为红，g为黑，u不存在/u存在且为黑

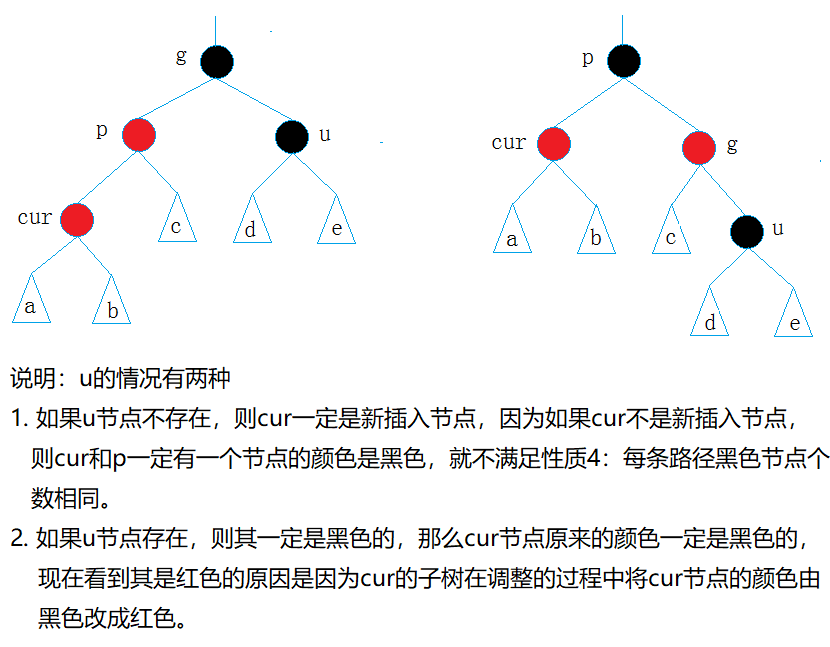
image-20230215151246360

如果不存在叔叔结点u，那么是这样的结构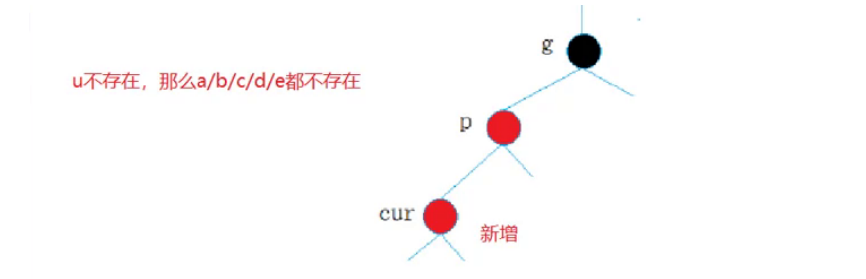：image-20230215153215295

此时，新增的cur节点为红，那我们必须想办法将p变黑，此时就可以考虑将g为轴进行旋转的方式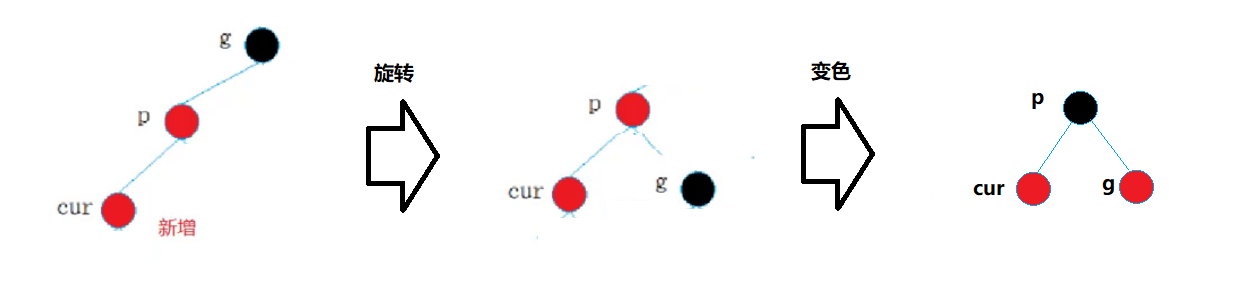image-20230215153745528

这样，就可以使其满足红黑树的结构了，u结点存在且为黑和此同理。

接下来看看步骤：

p为g的左孩子，cur为p的左孩子，则g进行右单旋转；相反，
p为g的右孩子，cur为p的右孩子，则g进行左单旋转
p、g变色–p变黑，g变红

情况3：双旋

  • cur为红，p为红，g为黑，u不存在/u存在且为黑

看似与情况二一样，实际上区别是cur插入的左右不同。情况2为左，情况3为右。

image-20230215155228807

和上篇中的AVL一样，对于这种弯的结构，只进行一次旋转是不可能成功的，因此需要进行两部旋转，上图只旋转了一次，变成了情况2，因此需要再旋转一次，就能满足红黑树结构的性质。

步骤：

  1. p为g的左孩子，cur为p的右孩子，则针对p做左单旋转；相反，p为g的右孩子，cur为p的左孩子，则针对p做右单旋转。
    则转换成了情况2。转换成情况2之后，再根据情况2的步骤继续旋转：
  2. p为g的左孩子，cur为p的左孩子，则g进行右单旋转；相反，p为g的右孩子，cur为p的右孩子，则g进行左单旋转
    p、g变色–p变黑，g变红

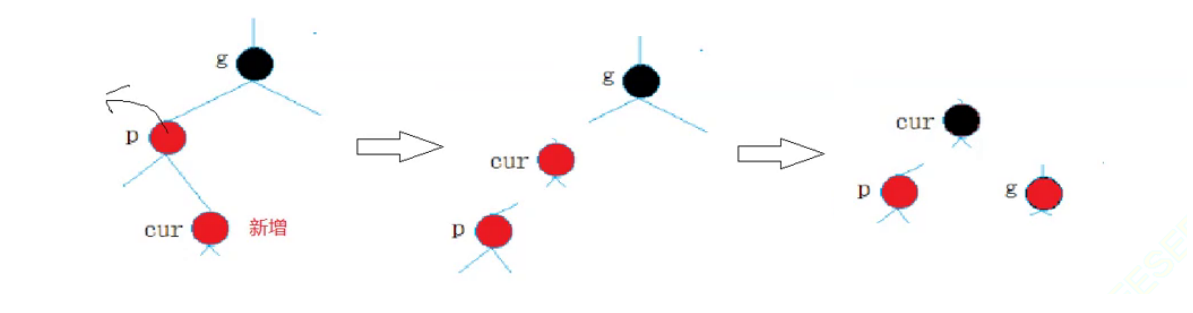
image-20230215161337990

注意，经过左旋，变色位置不变，但对应位置的结点变了，因此在代码编写时需注意这个问题。

插入的代码实现：

注：Insert单拿出来观察，其利用的旋转函数与AVL一样，只不过去掉了平衡因子。

bool Insert(const pair<K, V>& kv)
{
    if (_root == nullptr)
    {
        _root = new Node(kv);
        _root->_col = BLACK;//根节点为黑色
        return true;
    }

    Node* parent = nullptr;
    Node* cur = _root;
    while (cur)
    {
        if (cur->_kv.first < kv.first)
        {
            parent = cur;
            cur = cur->_right;
        }
        else if (cur->_kv.first > kv.first)
        {
            parent = cur;
            cur = cur->_left;
        }
        else
        {
            return false;
        }
    }

    cur = new Node(kv);
    cur->_col = RED;//重要，插入的结点初始化成红色
    if (parent->_kv.first < kv.first)
    {
        parent->_right = cur;
        cur->_parent = parent;
    }
    else
    {
        parent->_left = cur;
        cur->_parent = parent;
    }

    while (parent && parent->_col == RED)//如果父亲的颜色为红，才需要去处理
    {
        Node* grandfather = parent->_parent;//找到祖父才能找到叔叔
        if (parent == grandfather->_left)
        {
            Node* uncle = grandfather->_right;
            //看叔叔颜色
            //情况1：uncle存在且为红
            if (uncle && uncle->_col == RED)
            {
                parent->_col = uncle->_col = BLACK;
                grandfather->_col = RED;

                cur = grandfather;
                parent = cur->_parent;
            }
            else//情况2或3：不用考虑叔叔的问题，即叔叔为空还是为黑
            {
                if (cur == parent->_left)//情况2
                {
                    //     g
                    //   p
                    // c
                    RotateR(grandfather);
                    parent->_col = BLACK;
                    grandfather->_col = RED;
                }
                else//情况3
                {
                    //     g
                    //   p
                    //     c
                    RotateL(parent);
                    RotateR(grandfather);
                    cur->_col = BLACK;
                    grandfather->_col = RED;
                }
                break;
            }
        }
        else//与上述代码的左右反过来了而已，步骤一样但左右相反。
        {
            Node* uncle = grandfather->_left;
            //情况1
            if (uncle && uncle->_col == RED)
            {
                parent->_col = uncle->_col = BLACK;
                grandfather->_col = RED;

                cur = grandfather;
                parent = cur->_parent;
            }
            else//情况2和3
            {
                //  g
                //     p
                //        c
                if (cur == parent->_right)
                {
                    RotateL(grandfather);
                    parent->_col = BLACK;
                    grandfather->_col = RED;
                }
                else
                {
                    //  g
                    //     p
                    //   c
                    RotateR(parent);
                    RotateL(grandfather);
                    cur->_col = BLACK;
                    grandfather->_col = RED;
                }
            }
        }
    }
    _root->_col = BLACK;
    return true;
}

此外，有插入就有删除，删除是插入的反向思维。删除太难了，不用学。真想了解看这个，但是没有代码：红黑树 - Never - 博客园 (cnblogs.com)

四.红黑树的验证

红黑树的检测分为两步：

  1. 检测其是否满足二叉搜索树(中序遍历是否为有序序列)
  2. 检测其是否满足红黑树的性质

函数代码：

bool IsBalance()//检查是否为红黑树结构
{
    if (_root == nullptr)
    {
        return true;
    }

    if (_root->_col != BLACK)
    {
        return false;
    }

    int ref = 0;
    Node* left = _root;
    while (left)
    {
        if (left->_col == BLACK)
        {
            ++ref;
        }

        left = left->_left;
    }
    //遍历这棵树，就好了，检查是否存在连续的红结点。
    //检查父亲，因为孩子不一定有，但是一定有父亲
    return Check(_root, 0, ref);
}
bool Check(Node* root, int blackNum, int ref)
{
    if (root == nullptr)
    {
        if (blackNum != ref)
        {
            cout << "违反规则：一条路径上的黑色节点数量不同" << endl;
            return false;
        }
        return true;
    }

    if (root->_col == RED && root->_parent->_col == RED)
    {
        cout << "违反规则，出现连续红色结点" << endl;
    }
    if (root->_col == BLACK)
    {
        ++blackNum;
    }
    return Check(root->_left, blackNum, ref)
        && Check(root->_right, blackNum, ref);
}

五.红黑树实现代码（完整）

随机插入构建红黑树：
在这里插入图片描述
以升序插入构建红黑树：
在这里插入图片描述
以降序插入构建红黑树：
在这里插入图片描述

RBTree.h

#pragma once

enum Color//颜色采用枚举，但STL库采用的是特殊的bool值，后续会看
{
	RED,//0
	BLACK//1
};

template<class K, class V>
struct RBTreeNode
{
	pair<K, V> _kv;
	RBTreeNode<K, V>* _left;
	RBTreeNode<K, V>* _right;
	RBTreeNode<K, V>* _parent;
	Color _col;

	RBTreeNode(const pair<K, V>& kv)
		:_kv(kv)
		, _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _col(RED)
	{}

};

template<class K, class V>
class RBTree
{
	typedef RBTreeNode<K, V> Node;
public:
	bool Insert(const pair<K, V>& kv)
	{
		if (_root == nullptr)
		{
			_root = new Node(kv);
			_root->_col = BLACK;//根节点为黑色
			return true;
		}

		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_kv.first < kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_kv.first > kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}

		cur = new Node(kv);
		cur->_col = RED;//重要，插入的结点初始化成红色
		if (parent->_kv.first < kv.first)
		{
			parent->_right = cur;
			cur->_parent = parent;
		}
		else
		{
			parent->_left = cur;
			cur->_parent = parent;
		}

		while (parent && parent->_col == RED)//如果父亲的颜色为红，才需要去处理
		{
			Node* grandfather = parent->_parent;//找到祖父才能找到叔叔
			if (parent == grandfather->_left)
			{
				Node* uncle = grandfather->_right;
				//看叔叔颜色
				//情况1：uncle存在且为红
				if (uncle && uncle->_col == RED)
				{
					parent->_col = uncle->_col = BLACK;
					grandfather->_col = RED;

					cur = grandfather;
					parent = cur->_parent;
				}
				else//情况2或3：不用考虑叔叔的问题，即叔叔为空还是为黑
				{
					if (cur == parent->_left)//情况2
					{
						//     g
						//   p
						// c
						RotateR(grandfather);
						parent->_col = BLACK;
						grandfather->_col = RED;
					}
					else//情况3
					{
						//     g
						//   p
						//     c
						RotateL(parent);
						RotateR(grandfather);
						cur->_col = BLACK;
						grandfather->_col = RED;
					}
					break;
				}
			}
			else//与上述代码的左右反过来了而已，步骤一样但左右相反。
			{
				Node* uncle = grandfather->_left;
				//情况1
				if (uncle && uncle->_col == RED)
				{
					parent->_col = uncle->_col = BLACK;
					grandfather->_col = RED;

					cur = grandfather;
					parent = cur->_parent;
				}
				else//情况2和3
				{
					//  g
					//     p
					//        c
					if (cur == parent->_right)
					{
						RotateL(grandfather);
						parent->_col = BLACK;
						grandfather->_col = RED;
					}
					else
					{
						//  g
						//     p
						//   c
						RotateR(parent);
						RotateL(grandfather);
						cur->_col = BLACK;
						grandfather->_col = RED;
					}
				}
			}
		}

		_root->_col = BLACK;
		return true;

	}

	//旋转代码和AVL一样，只是去掉了平衡因子
	void RotateL(Node* parent)//左单旋
	{
		//1.记录subR, subRL
		Node* subR = parent->_right;
		Node* subRL = subR->_left;


		parent->_right = subRL;
		if (subRL)//subRL不为空则需要连接到parent
		{
			subRL->_parent = parent;
		}

		Node* ppNode = parent->_parent;//记录保存
		subR->_left = parent;
		parent->_parent = subR;

		if (ppNode == nullptr)//说明根节点变化
		{
			_root = subR;
			_root->_parent = nullptr;
		}
		else//如果是局部子树
		{
			//判断ppNode之前是左连接还是右连接
			if (ppNode->_left == parent)
			{
				ppNode->_left = subR;
			}
			else
			{
				ppNode->_right = subR;
			}
			subR->_parent = ppNode;
		}

	}

	void RotateR(Node* parent)//右单旋
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;

		parent->_left = subLR;
		if (subLR)
		{
			subLR->_parent = parent;
		}

		Node* ppNode = parent->_parent;
		subL->_right = parent;
		parent->_parent = subL;

		if (ppNode == nullptr)
		{
			_root = subL;
			_root->_parent = nullptr;
		}
		else
		{
			if (ppNode->_left == parent)
			{
				ppNode->_left = subL;
			}
			else
			{
				ppNode->_right = subL;
			}
			subL->_parent = ppNode;
		}
	}

	void Inorder()
	{
		_Inorder(_root);
	}

	bool IsBalance()//检查是否为红黑树结构
	{
		if (_root == nullptr)
		{
			return true;
		}

		if (_root->_col != BLACK)
		{
			return false;
		}

		int ref = 0;
		Node* left = _root;
		while (left)
		{
			if (left->_col == BLACK)
			{
				++ref;
			}

			left = left->_left;
		}
		//遍历这棵树，就好了，检查是否存在连续的红结点。
		//检查父亲，因为孩子不一定有，但是一定有父亲
		return Check(_root, 0, ref);
	}

private:
	bool Check(Node* root, int blackNum, int ref)
	{
		if (root == nullptr)
		{
			if (blackNum != ref)
			{
				cout << "违反规则：一条路径上的黑色节点数量不同" << endl;
				return false;
			}
			return true;
		}

		if (root->_col == RED && root->_parent->_col == RED)
		{
			cout << "违反规则，出现连续红色结点" << endl;
		}
		if (root->_col == BLACK)
		{
			++blackNum;
		}
		return Check(root->_left, blackNum, ref)
			&& Check(root->_right, blackNum, ref);
	}

	void _Inorder(Node* root)
	{
		if (root == nullptr)
		{
			return;
		}

		_Inorder(root->_left);
		cout << root->_kv.first << ":" << root->_kv.second << endl;
		_Inorder(root->_right);
	}
	Node* _root = nullptr;
};

void TestRBTree1()
{
	int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
	RBTree<int, int> t;
	for (auto e : a)
	{
		t.Insert(make_pair(e, e));
	}

	t.Inorder();


}

Test.cpp

#include<iostream>
#include<string>
#include<map>
#include<assert.h>
using namespace std;
#include"RBTree.h"
int main()
{
	TestRBTree1();
	return 0;
}

六.红黑树与AVL树的比较

红黑树和AVL树都是高效的平衡二叉树，增删改查的时间复杂度都是O( l o g 2 N log_2 N log2​N)，红黑树不追求绝对平衡，其只需保证最长路径不超过最短路径的2倍，相对而言，降低了插入和旋转的次数，所以在经常进行增删的结构中性能比AVL树更优，而且红黑树实现比较简单，所以实际运用中红黑树更多。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/357983.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Docker入门和安装教程

Docker入门和安装教程

一、Docker入门简介 Docker 是一个基于GO语言开发的开源的应用容器引擎&#xff0c;让开发者可以打包他们的应用以及依赖包到一个可移植的容器中&#xff0c;然后发布到任何流行的Linux机器上&#xff0c;也可以实现虚拟化。 容器是完全使用沙箱机制&#xff0c;相互之间不会…
阅读更多...
关于如何在 Grafana 绘制 Apache Hudi Metrics 仪表盘的教程

关于如何在 Grafana 绘制 Apache Hudi Metrics 仪表盘的教程

文章目录前言下载 Prometheus下载 PushgatewayPrometheus 集成 PushgatewayPushgateway 后台执行Prometheus 后台执行在Prometheus中配置PushgatewayApache Hudi Metrics中开启 Pushgateway 推送Grafana 安装和启动Grafana 新增 Apache Hudi Metrics 仪表盘添加 Prometheus 数据…
阅读更多...
批处理删除指定文件或文件夹

批处理删除指定文件或文件夹

声明&#xff1a;1-2节参考了 https://blog.csdn.net/weixin_43960383/article/details/1243673841. DEL1.1 DEL 的命令参数使用 del 命令能指定文件&#xff0c;Del (erase)[Drive:][Path]FileName指删除指定文件。指定要删除的文件或文件集的位置和名称。语法格式如下&#x…
阅读更多...
XML学习

XML学习

文章目录XML什么是XML?XML的作用&#xff1f;XML语法文档声明XML注释元素&#xff08;标签&#xff09;xml属性语法规则5.4、xml解析技术介绍dom4j 解析技术&#xff08;重点&#xff09;dom4j 编程步骤&#xff1a;使用遍历标签 获取所有标签中的内容&#xff08;重点&#x…
阅读更多...
第十三届蓝桥杯国赛 C++ C 组 Java A 组 C 组 Python C 组 E 题——斐波那契数组（三语言代码AC）

第十三届蓝桥杯国赛 C++ C 组 Java A 组 C 组 Python C 组 E 题——斐波那契数组（三语言代码AC）

目录1.斐波那契数组1.题目描述2.输入格式3.输出格式4.样例输入5.样例输出6.数据范围7.原题链接2.解题思路3.Ac_code1.Java2.C3.Python1.斐波那契数组 1.题目描述 如果数组 A(a0,a1,⋯.an−1)A(a_0,a_1,⋯.a_{n-1})A(a0​,a1​,⋯.an−1​)满足以下条件, 就说它是一个斐波那契…
阅读更多...
如何在类中定义构造方法？

如何在类中定义构造方法？

在一个类中定义的方法如果同时满足以下三个条件&#xff0c;该方法称为构造方法&#xff0c;具体如下&#xff1a;1、方法名与类名相同2、在方法名的前面没有返回值类型的声明3、在方法中不能使用return语句返回一个值接下来通过一个案例来演示如何在类中定义构造方法&#xff…
阅读更多...
闪光桐人の实习日记（2023年2月20-27日）

闪光桐人の实习日记（2023年2月20-27日）

前往闪闪の小窝以获得更好的阅读和评论体验 文章目录2023年2月20日&#xff08;Vue入门&#xff09;概念Vue基础Vue中的MVVMVue的体验Vue的生命周期Vue指令Vue组件VueRouter前后端路由的区别工作原理两种模式比较route跟router的区别路由属性导航守卫Vuex概述5种基本对象基本使…
阅读更多...
C语言编程规范 第二部分

C语言编程规范 第二部分

2、头文件对于C语言来说&#xff0c;头文件的设计体现了大部分的系统设计。不合理的头文件布局是编译时间过长的根因&#xff0c;不合理的头文件实际上反映了不合理的设计。 1、头文件中适合放置接口的声明&#xff0c;不适合放置实现头文件是模块&#xff08;Module&#xff…
阅读更多...
【数据结构】时间复杂度和空间复杂度

【数据结构】时间复杂度和空间复杂度

&#x1f307;个人主页&#xff1a;平凡的小苏 &#x1f4da;学习格言&#xff1a;别人可以拷贝我的模式&#xff0c;但不能拷贝我不断往前的激情 &#x1f6f8;C语言专栏&#xff1a;https://blog.csdn.net/vhhhbb/category_12174730.html 小苏希望大家能从这篇文章中收获到许…
阅读更多...
苹果手机怎么设置闹钟铃声？更改为歌曲铃声，亲测有效

苹果手机怎么设置闹钟铃声？更改为歌曲铃声，亲测有效

很不是有很多小伙伴每天早上都被苹果手机刺耳的“雷达”闹钟铃声给吵醒呢&#xff1f;想要更换一个舒缓的闹钟铃声&#xff0c;却发现自己鼓捣半天却无法更换喜欢的歌曲闹钟铃声。苹果手机怎么设置闹钟铃声&#xff1f;下面小编就来分享如何将苹果手机的闹钟铃声设置成歌曲铃声…
阅读更多...
【docker】拉取镜像环境报错解决#ERROR: Get https://registry-1.docker.io/v2/

【docker】拉取镜像环境报错解决#ERROR: Get https://registry-1.docker.io/v2/

&#x1f341;博主简介   &#x1f3c5;云计算领域优质创作者   &#x1f3c5;华为云开发者社区专家博主   &#x1f3c5;阿里云开发者社区专家博主 &#x1f48a;交流社区&#xff1a;运维交流社区 欢迎大家的加入&#xff01; 文章目录问题报错原因解决方法问题 ERROR…
阅读更多...
简单的认识 Vue(vue-cli安装、node安装、开发者工具)

简单的认识 Vue(vue-cli安装、node安装、开发者工具)

Vue1、Vue 与其他框架的对比及特点1.1 Vue.js 是什么1.2 作者1.3 作用1.4 Vue 与其他框架的对比2、安装 Vue 的方法2.1 CDN 引入2.2 脚手架工具2.3 vue 开发者工具安装3、创建第一个实例4、理解 Vue 的 MVVM 模式5、数据双向绑定5.1 感受响应式实验总结1、Vue 与其他框架的对比…
阅读更多...
Flutter WebView 如何与 h5 同步登录状态

Flutter WebView 如何与 h5 同步登录状态

大家好&#xff0c;我是 17。 Flutter WebView 一共三篇文章 在 Flutter 中使用 webview_flutter 4.0 | js 交互Flutter WebView 性能优化&#xff0c;让 h5 像原生页面一样优秀Flutter WebView 如何与 h5 同步登录状态 本篇是第 3 篇&#xff0c;讲下 Flutter WebView 与 h…
阅读更多...
Python|每日一练|动态规划|图算法|散列表|数组|双指针|单选记录：不同路径|求两个给定正整数的最大公约数和最小公倍数|删除有序数组中的重复项

Python|每日一练|动态规划|图算法|散列表|数组|双指针|单选记录：不同路径|求两个给定正整数的最大公约数和最小公倍数|删除有序数组中的重复项

1、不同路径&#xff08;数学&#xff0c;动态规划&#xff09; 一个机器人位于一个 m x n 网格的左上角 &#xff08;起始点在下图中标记为 “Start” &#xff09;。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角&#xff08;在下图中标记为 “Finish”…
阅读更多...
【大数据基础】Linux常用命令

【大数据基础】Linux常用命令

参考资料&#xff1a; https://www.runoob.com/w3cnote/linux-common-command-2.html 1、ls命令 就是 list 的缩写&#xff0c;通过 ls 命令不仅可以查看 linux 文件夹包含的文件&#xff0c;而且可以查看文件权限(包括目录、文件夹、文件权限)查看目录信息等等。 ls -a 列…
阅读更多...
LockSupport常用方法源码分析

LockSupport常用方法源码分析

前言&#xff1a;本文将介绍LockSupport类中的方法和部分源码&#xff0c;以及面试常问到的一个小问题&#xff0c;感兴趣的大佬可以指点下。 希望能够加深自己的印象以及帮助到其他的小伙伴儿们&#x1f609;&#x1f609;。 如果文章有什么需要改进的地方还请大佬不吝赐教&am…
阅读更多...
uniapp项目引入vant2遇到报错Uncaught ReferenceError: require is not defined完美解决方案

uniapp项目引入vant2遇到报错Uncaught ReferenceError: require is not defined完美解决方案

一、问题描述 我用的是Vue2版本的uniapp项目&#xff0c;以下是Vant官方提供的安装方法&#xff0c;使用npm安装到uniapp项目中。 Vant官网&#xff1a;https://vant-contrib.gitee.io/vant/v2/#/zh-CN/quickstart 安装完成得到以下模块 官方提供的引入单个组件的方案 我需要引…
阅读更多...
Vision Transformer(ViT) 2: 应用及代码讲解

Vision Transformer(ViT) 2: 应用及代码讲解

文章目录1. 代码讲解1.1 PatchEmbed类1&#xff09;__init__ 函数2) forward 过程1.2 Attention类1&#xff09;__init__ 函数2&#xff09;forward 过程1.3 MLP类1&#xff09;__init__ 函数2&#xff09;forward函数1.4 Block类1&#xff09;__init__ 函数2&#xff09;forwa…
阅读更多...
MATLAB曲线拟合工具箱

MATLAB曲线拟合工具箱

MATLAB曲线拟合工具箱一、MATLAB曲线拟合工具箱1.导出拟合后的曲线数据2.调用m文件中的函数3.显示5位有效数字二、参考链接一、MATLAB曲线拟合工具箱 1.导出拟合后的曲线数据 生成代码后&#xff0c;默认函数名为createFit&#xff0c;可以自行修改&#xff0c;直接保存&#…
阅读更多...
Allegro如何重命名光绘操作指导

Allegro如何重命名光绘操作指导

Allegro如何重命名光绘操作指导 在做PCB设计的时候，光绘设置是输出生产文件必要的流程，设置好光绘之后，如何对光绘重新命名，如下图 如何把L1改成TOP，L6改成BOTTOM，具体操作步骤如下 点击Manufacture选择Artwork
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023