第二十二章 四大查找算法
目录
第二十二章 四大查找算法
●前言
●查找算法
●一、顺序查找法
1.什么是顺序查找法?
2.案例实现
●二、二分查找法
1.什么是二分查找法?
2.案例实现
●三、插值查找法
1.什么是插值查找法?
2.案例实现
●四、斐波那契查找法
1.什么是斐波那契查找法?
2.案例实现
●总结
前言
在数据处理的过程中,能否在最短时间内去找到目的数据,是编程开发人员非常值得关心的一个问题。所谓查找,也被称为搜索,它是指从数据文件中找出满足某些条件的记录。在数据结构中描述算法时习惯用“查找”,而在搜索引擎中找信息或资料时习惯用“搜索”。我们在电话簿中查找某人的电话号码,电话簿就像是数据文件库,而姓名就是去查找电话号码的键值。我们经常使用的搜索引擎所设计的Spider程序(网页抓取程序爬虫)会主动经由网站上的超链接“爬行”到另一个网站,搜集每个网站上的信息并且收录到数据库中,这其中就涉及到了今天要讲的查找算法。
查找算法
在查找算法中,比较常见的有顺序法、二分法、插入法和斐波那契法等。查找的操作和算法有关,具体的操作方式和进行方式与所选择的数据结构有关。计算机查找数据的优点就是快速,但是对于不同程度下的数据量,查找可以分为内部查找(数据量较小的文件)和外部查找(数据量较大的文件)。影响查找时间长短的主要因素有算法,数据存储的方式以及结构。查找可以分为静态查找和动态查找。静态查找是指数据元素在查找的过程中不会有添加,删除,更新等操作。动态查找是指所查找的数据在查找过程中会经常地添加,删除或更新。
一、顺序查找法
1.什么是顺序查找法?
(1)简要介绍
顺序查找法是一种比较简单的查找法。该算法就是利用了计算机便于处理大量数据的这一特点,从而来进行实现的。该方法的优点就是文件在查找前不需要进行任何处理与排序;而缺点是查找的速度比较慢,因为无论数据顺序是什么情况,它都需要从头到尾都去遍历一遍。如果数据元素没有重复,那么找到数据元素就可以中止查找。说明最差的情况是n次查找,最好的情况下是1次查找。
(2)具体情况
在8个数据元素中,去顺序查找元素89。情况如下图所示:
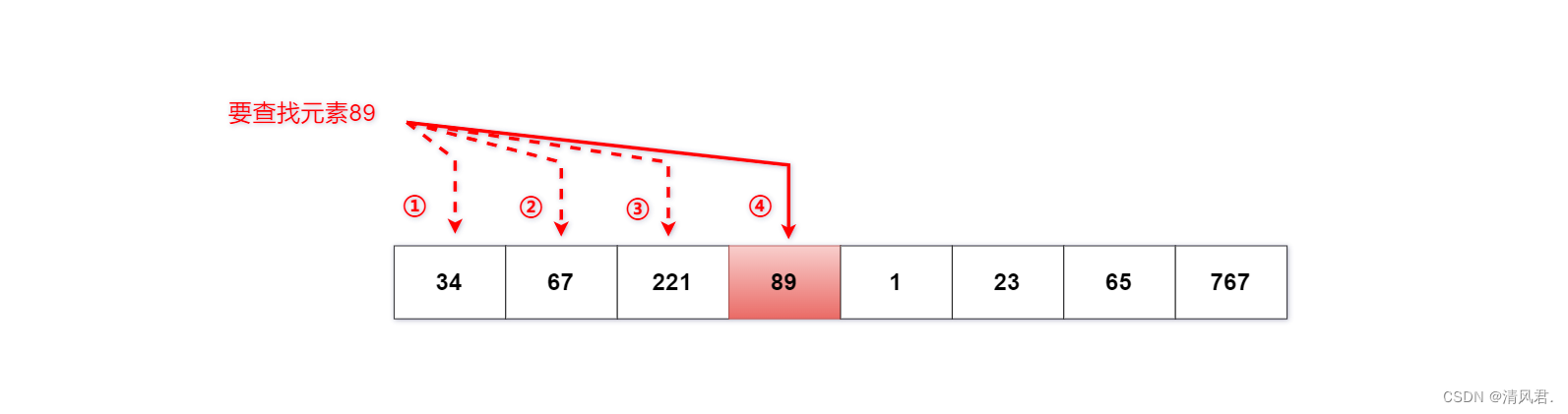
对于大量重复的数据元素来说,顺序查找法一般是不会使用的,因为它的时间效率极低并且可能会因为元素中的重复项而造成错误。但是对于少量的数据元素来说,这无疑是一种非常快又准确性高的简单方法。
(3)算法分析
①时间复杂度:如果数据没有重复且找到数据就可以中止,那么在最差情况下就是未找到数据,进行了n次比较,所以时间复杂度为O(n)。
②当数据量很大时,不适合使用顺序查找法。如果事先预估到所查找的数据在文件前面的部分,就可以减少查找的时间。
③在平均情况下,假设数据出现的概率相等,则需要进行(n+1)/2次比较。
2.案例实现
(1)范例情况:用随机法生成80个1~100的整数,用顺序查找法去查找我们指定元素是否存在,如果存在说明其所在的位置。
(2)代码展示:
#include<iostream>
#include<cstdlib>
using namespace std;
class order {
public:
int data[80];
int val = 0;
//构造函数 随机给data中分配数据
order() {
for (int i = 0; i < 80; i++)
data[i] = (rand() % 100) + 1;
}
void order_start() {
cout << "请输入要猜测的数:";
cin >> val;
for (int i = 0; i < 80; i++)
{
if (data[i] == val) {
cout << "该数" << data[i] << "存在 所在位置为" << i + 1 << endl;
val = 0;
}
}
if (val != 0)
cout << "该数不存在" << endl;
}
//析构函数 展现所有元素
~order() {
cout << "所有随机数据元素如下:" << endl;
for (int i = 0; i < 80; i++)
cout << data[i] << "[" << i << "]" << " ";
}
};
int main()
{
order o;
while (o.val != -1)
{
o.order_start();
}
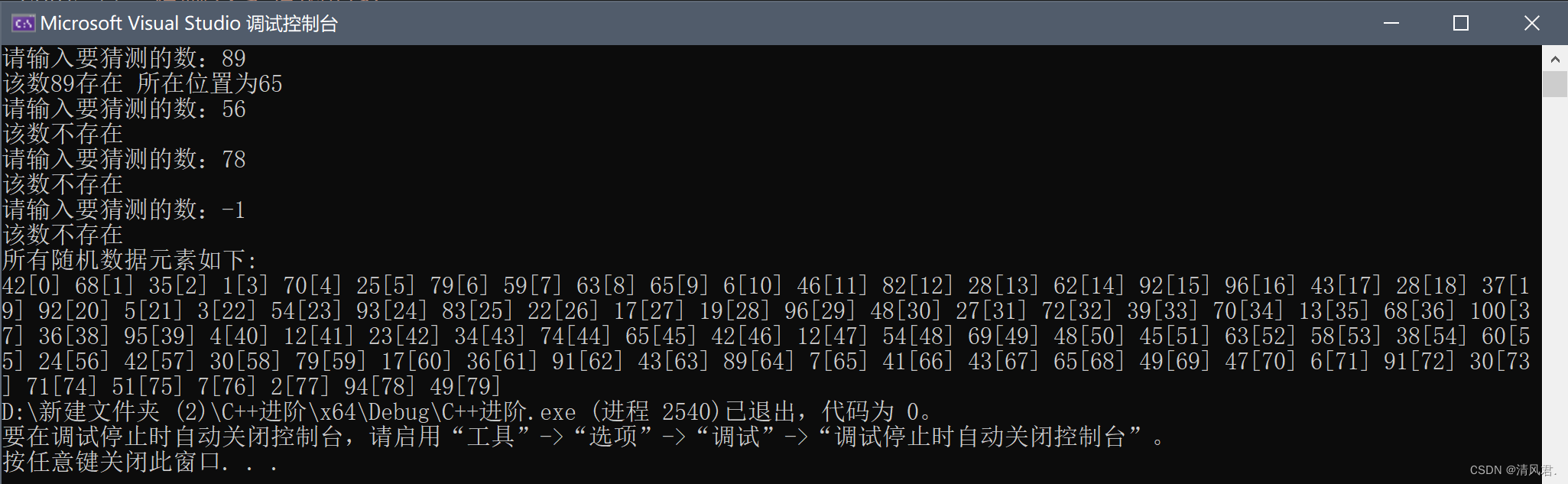
}(3)结果展示:
二、二分查找法
1.什么是二分查找法?
(1)简要介绍
如果一组数据已经事先排好了顺序,那么就可以用二分查找法来进行查找。二分查找法的基本方法就是将数据分成两等份,比较目标寻找值与中间值的大小。如果小于中间值,那么我们就可以确定要寻找的数据在前半部分,否则在后半部分。重复上述步骤将其分割直到找到或确定不存在为止。
(2)具体情况
用二分查找法对已经完成排序的一组数列,查找其元素101所在的位置。具体情况如下图所示:
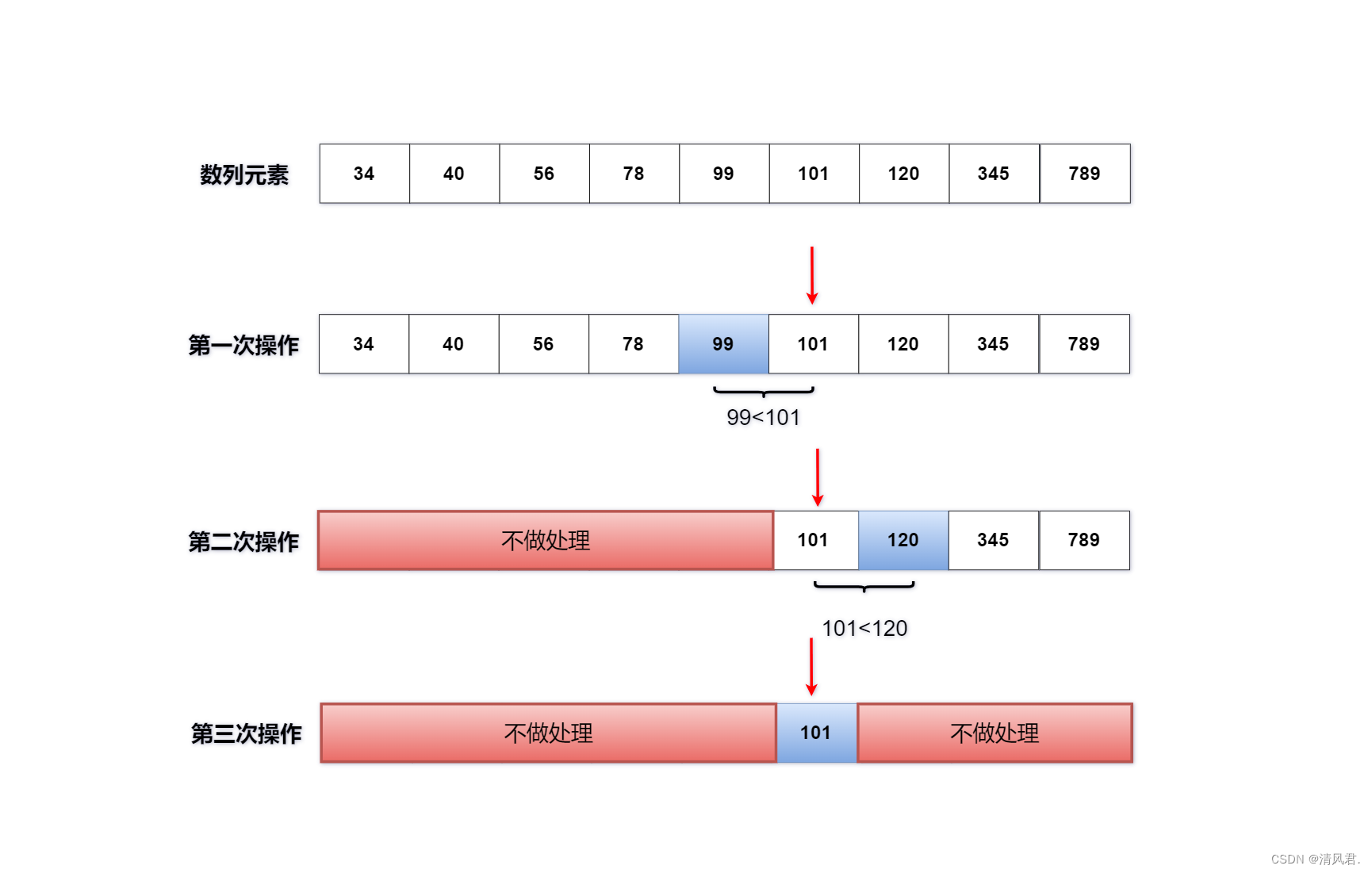
(3)算法分析
①时间复杂度:因为每次的查找都会比上一次查找少一半的范围,所以最多只需比较(log2^n)+1或(log2^(n+1))次,时间复杂度O(log2^n)。
②二分查找法必须是经过排序的数列,且数据元素都要加载到内存中才能进行查找。
③二分查找法适用于不需要增删的静态数据。
2.案例实现
(1)范例程序:用二分查找法查找10个1~10随机数据中指定数据元素的位置,并且输出随机产生的这10个数据。
(2)代码展示:
#include<iostream>
using namespace std;
#define size 10
class dichotomy {
public:
int data[size];
int val = 0;
dichotomy() {
for (int i = 0; i < size; i++)
data[i] = (rand() % 10) + 1;
}
void sort() {
for (int i = 0; i < size-1; i++) {
for (int j = i+1; j < size; j++) {
if (data[i] > data[j])
{
int temp;
temp = data[i];
data[i] = data[j];
data[j] = temp;
}
}
}
}
void dichotomy_start(int len_left,int len_right){
int record=0;
while (len_left <= len_right )
{
int mid = (len_right + len_left) / 2;
if (val < data[mid]) {
cout << "目标数在中间值的左边" << endl;
len_right = mid - 1;
}
else if (val > data[mid]) {
cout << "目标数在中间值的右边" << endl;
len_left = mid + 1;
}
else if(val==data[mid]){
cout << "在第" << mid + 1 << "个位置处找到了" << "该元素" << data[mid] << endl;
val = 1;
break;
}
}
if (val != 1) {
cout << "随机产生的这几个数中不存在要猜测的这个数值" << endl;
}
}
~dichotomy() {
cout << "所有随机数据元素如下:" << endl;
for (int i = 0; i < size; i++)
cout << data[i] << "[" << i << "]" << " ";
}
};
int main()
{
dichotomy d;
d.sort();
while (d.val!=-1)
{
cout << "请输入要猜测的数:";
cin >> d.val;
if (d.val != -1)
d.dichotomy_start(0, size - 1);
else
break;
}
}
(3)结果展示:
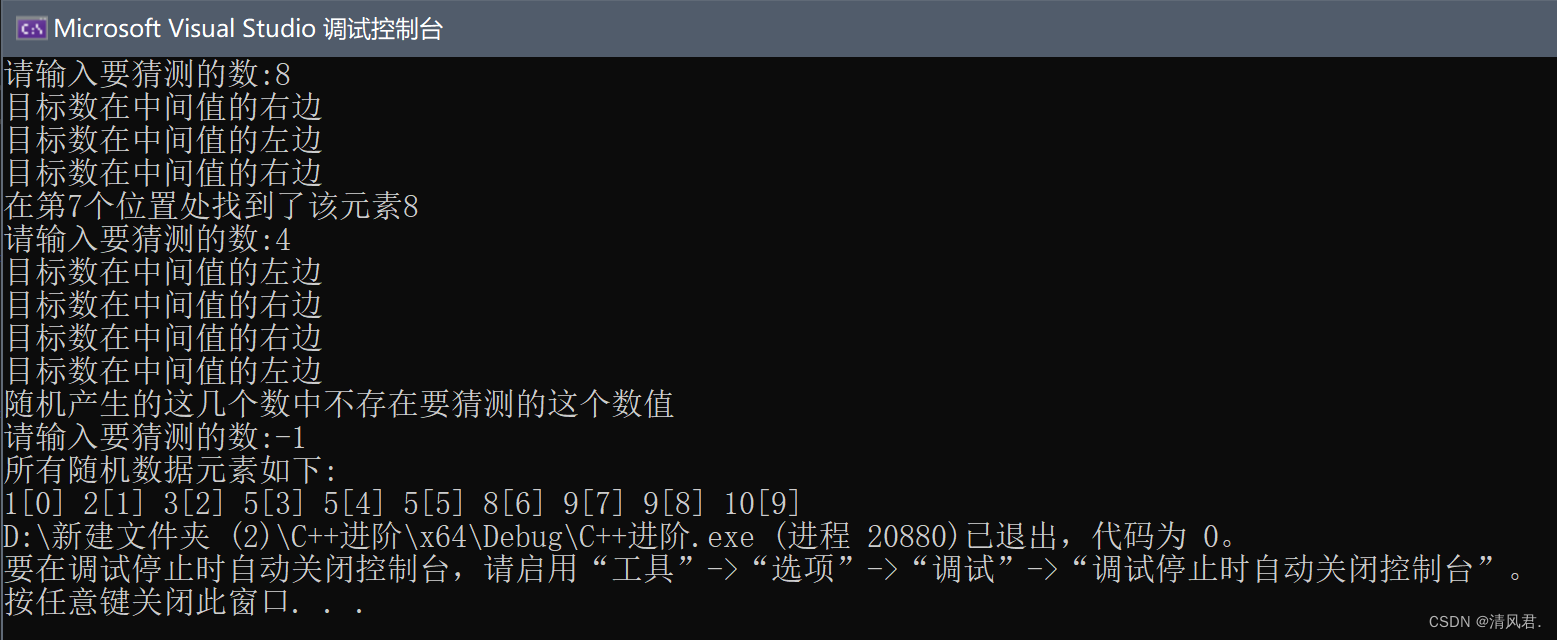
三、插值查找法
1.什么是插值查找法?
(1)简要介绍
插值查找法又被称为插补查找法,是对二分查找的进一步改进。它是按照数据位置的分布,利用公式去预测数据所在的位置,再用二分法的方式渐渐逼近。该查找法的公式如下:

其中,key是要去查找的键值,data[high],data[low]是剩余待查找记录中的最大值和最小值。特别注意:使用该查找算法之前需要对要排序的数据进行排序。
(2)具体情况
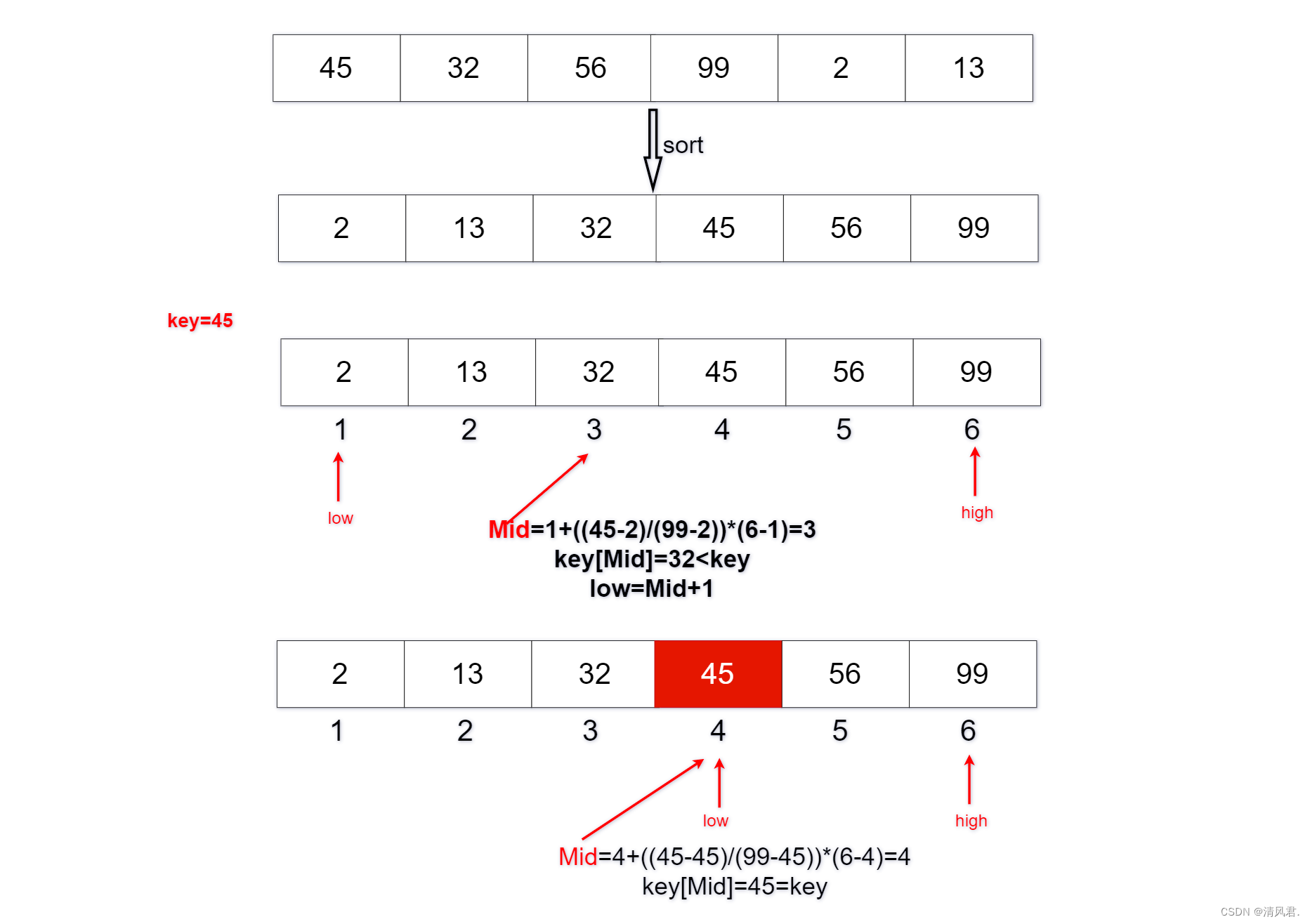
假设数据项为n,其插值查找法的步骤如下:
①讲记录从小到大的顺序给予1,2,...,n的编号;
②令low=1,high=n;
③当low<high时,重复执行步骤④和步骤⑤;
④令Mid=low+((key-data[low])/(data[high]-data[low]))*(high-low);
⑤若key<key[mid]且high≠Mid-1,则令high=Mid-1;
⑥若key>key[mid]且low≠Mid+1,则令low=Mid+1;
⑦若key=key[mid],则表示成功找到了键值的位置;
(3)算法分析
①插值查找法优于顺序查找法,如果数据的分布越平均,查找速度就越快,甚至可能第一次就找到数据。插值查找法的时间复杂度取决于数据的分布情况,平均而言优于O(log2^n)。
2.案例实现
①范例程序:用插值查找法去查找10个随机数据中,指定元素数据所在的位置。
②代码展示:
#include<iostream>
using namespace std;
class interpolation_search {
public:
int data[10];
int val = 0;
interpolation_search() {
for (int i = 0; i < 10; i++)
data[i] = (rand() % 10) + 1;
}
void sort() {
for (int i = 0; i < 10-1; i++)
{
for (int j = i + 1; j < 10; j++)
{
if (data[i] > data[j])
{
int temp;
temp = data[i];
data[i] = data[j];
data[j] = temp;
}
}
}
}
void interpolation_search_start() {
int low = 0, high = 9;
while (low<=high)
{
int mid = low + ((val - data[low]) / (data[high] - data[low])) * (high - low);
if (val < data[mid]) {
cout << "目标元素在mid的左边" << endl;
high = mid - 1;
}
if (val > data[mid]) {
cout << "目标元素在mid的右边" << endl;
low = mid + 1;
}
if (val == data[mid]) {
cout << "找到了该元素,该元素位置在" << mid + 1 << "处" << endl;
val = 1;
break;
}
}
if (val != 1) {
cout << "随机生成的数据中没有你要去查找的数据" << endl;
}
}
~interpolation_search() {
cout << "随机产生的数据元素如下" << endl;
for (int i = 0; i < 10; i++)
cout << data[i] << " ";
}
};
void text()
{
interpolation_search is;
is.sort();
while (is.val != -1)
{
cout << "请输入你要查找的数:";
cin >> is.val;
is.interpolation_search_start();
}
}
int main()
{
text();
}③结果展示:
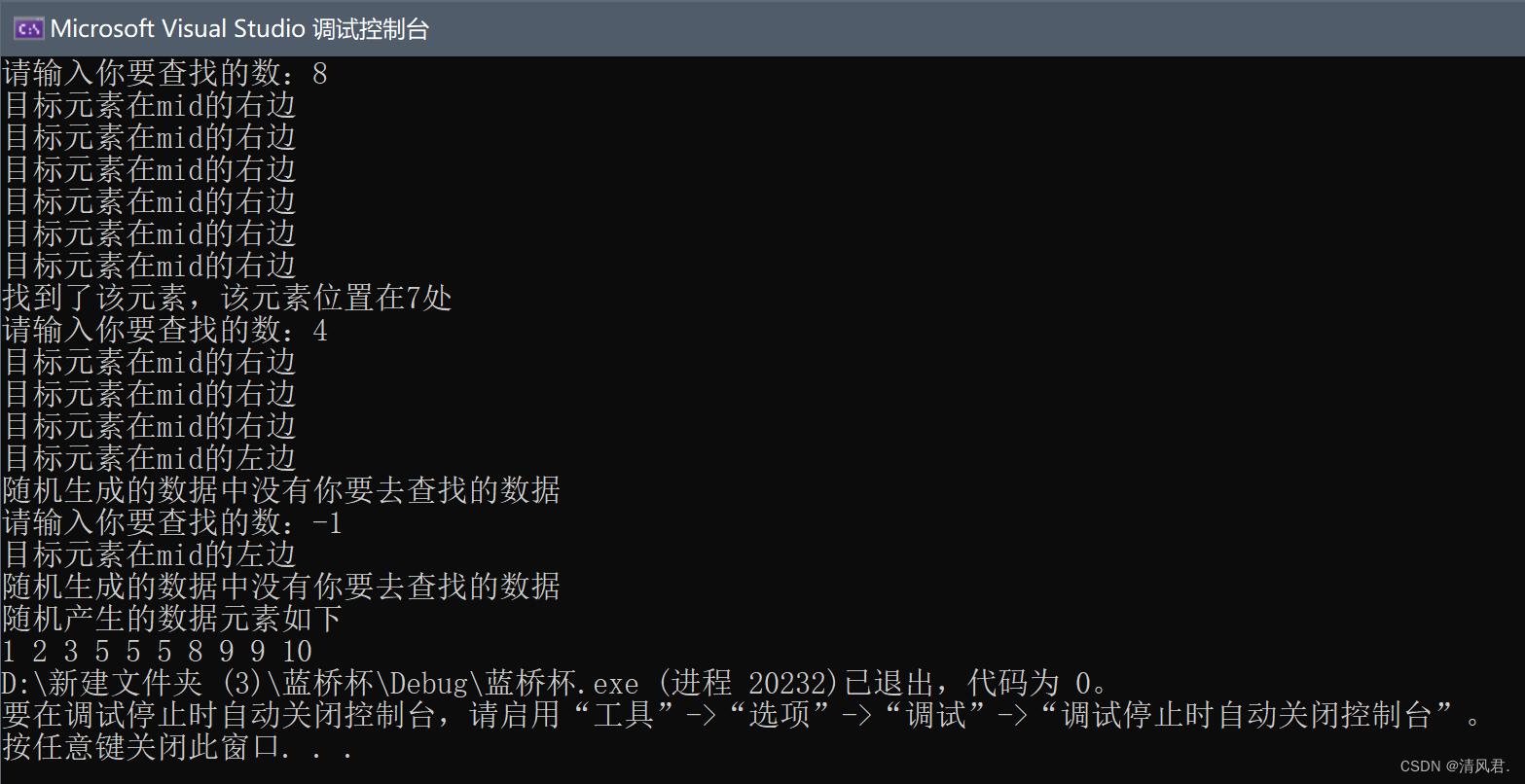
四、斐波那契查找法
1.什么是斐波那契查找法?
(1)简要介绍
斐波那契查找法又被称为斐氏查找法,该方法与二分法一样都是以分割范围来进行查找的,不同的是该方法不是以对半的方式来进行分割的,而是利用斐波那契级数(0、1、1、2、3、5、8、13、21、34、55、...)来进行分割的。该查找法的优点就是只需要用到加减运算,这从计算机运算的底层来看效率是相对较高的。并且该查找法会用到斐波那契树,所以我们应该先来了解该树的基本情况和特点。
(2)具体情况
斐波那契树的建立原则:
①斐波那契树的左右子树都是斐波那契树。
②斐波那契树的树根一定是一个斐波那契数,且子节点与父节点之间的差值的绝对值仍为斐波那契数。
③当k≥2时,斐波那契树的树根为Fib(k),左子树为(k-1)层斐波那契树,右子树为(k-2)层斐波那契树。
④当数据个数n确定时,若想确定斐波那契树的层数k为多少,必须找到一个最小的k值,使斐波那契层数的Fib(k+1)≥n+1。
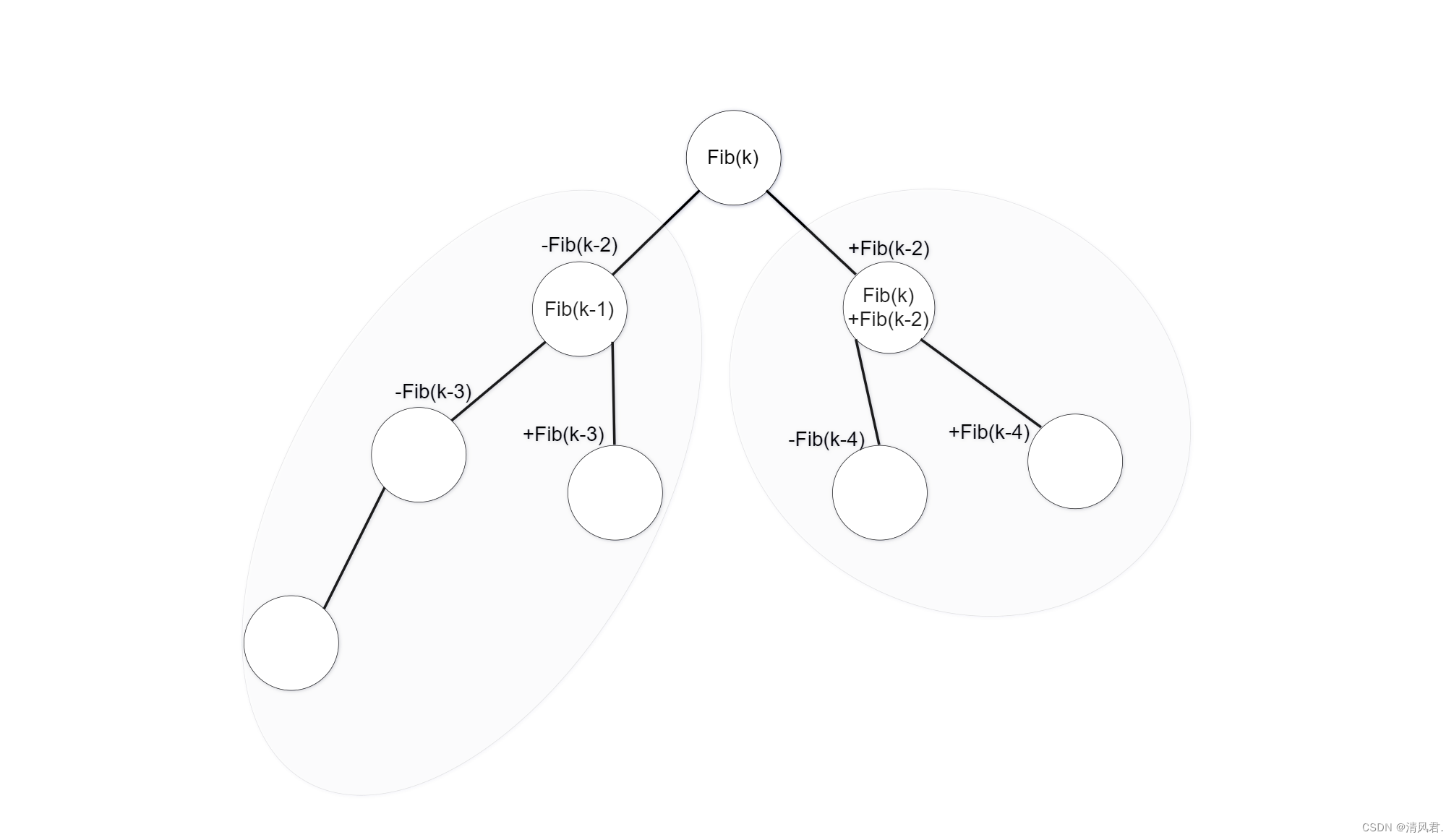
也就是说当数据个数为n,我们找到一个最小的斐波那契数Fib(k+1)使得Fib(k+1)>n+1时,Fib(k)就是这棵树的树根,而Fib(k-2)就是与左右子树开始的差值,左子树去减,右子树去加。例如去求取n=33的斐波那契树。由于n=33,则n+1=34为一棵斐波那契树。由斐波那契公式可得知Fib(0)=0,Fib(1)=1,Fib(2)=1,Fib(3)=2,Fib(4)=3,Fib(5)=5,Fib(6)=8,Fib(7)=13,Fib(8)=21,Fib(9)=34。可知Fib(k+1)≥n+1为Fib(8+1)=34,k=8所以建立二叉树的树根为Fib(8)=21。左子树的树根为Fib(8-1)=13;右子树的树根为Fib(8)+Fib(8-2)=21+8=29;从而依照上述步骤建立的斐波那契树如下图所示:
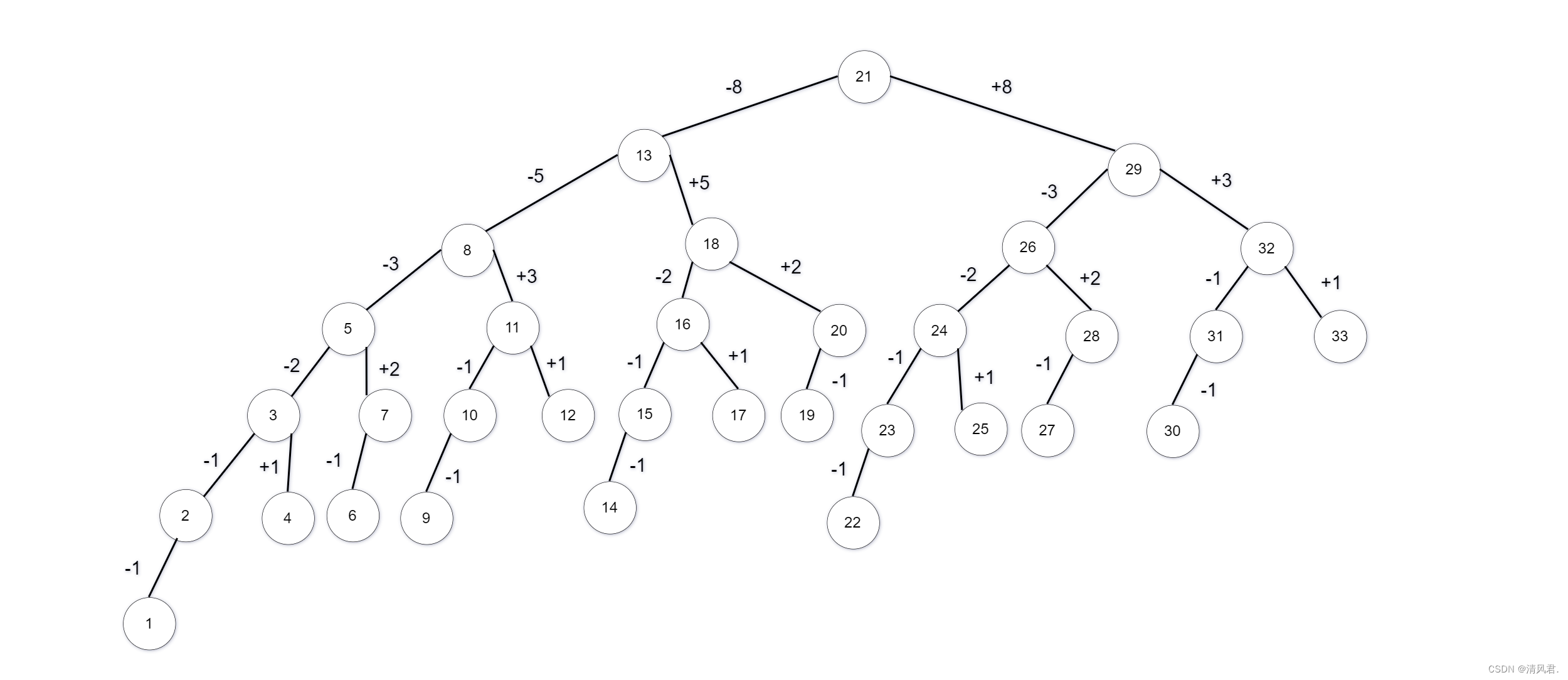
若我们要查找的键值为key,首先要去比较数组下标Fib(k)和键值key,此时就将会出现多种情况如下:
①key值较小,落在了1~Fib(k)-1位置上,所以继续去查找1~Fib(k)-1的数据;key值较大,落在了Fib(k)+1~Fib(k+1)-1的位置上,所以继续去查找Fib(k)+1~Fib(k+1)-1的数据。
②当键值与数组下标Fib(k)的值相等时,则表示成功的查找到了目标数据元素的位置。
(3)算法分析
① 斐波那契查找法虽然平均比较次数少于二分查找法,但在最坏的情况下还是二分查找法较快,并且斐波那契查找法相对复杂,因为它需要去额外产生一棵斐波那契树。
2.案例实现
①范例程序:用斐波那契树查找法去查找指定键值是否存在,并且如果存在其在哪个具体的位置。
②代码展示:
#include<iostream>
using namespace std;
#define size 10
class Fib {
public:
int data[size];
int val = 0;
Fib() {
for (int i = 0; i < size; i++)
data[i] = (rand() % 10) + 1;
}
int Fib_start(int n) {
if (n == 0 || n == 1)
return 1;
else
return Fib_start(n - 1) + Fib_start(n - 2);
}
int Fib_search_start() {
int index = 2;
while (Fib_start(index) <= size)
index++;
index--;
int rootnode = Fib_start(index);
int diff_1 = Fib_start(index - 1);
int diff_2 = rootnode - diff_1;
rootnode--;
while (1)
{
if (val == data[rootnode])
{
return rootnode;
}
else
{
if (index == 2)
return size;
if (val < data[rootnode])
{
rootnode = rootnode - diff_2;
int temp = diff_1;
diff_1 = diff_2;
diff_2 = temp - diff_2;
index = index - 1;
}
else
{
if (index == 3)
return size;
rootnode = rootnode + diff_2;
diff_1 = diff_1 - diff_2;
diff_2 = diff_2 - diff_1;
index = index - 2;
}
}
}
}
~Fib()
{
cout << "随机生成的所有数据情况如下" << endl;
for (int i = 0; i < 10; i++)
cout << data[i] << " ";
}
};
void text()
{
Fib f;
while (f.val != -1)
{
cout << "请输入要查找的值:";
cin >> f.val;
int count = f.Fib_search_start();
if(count==size)
cout << "没有找到该数据元素" << endl;
else
cout << "在第" << count + 1 << "个位置找到了该数据元素" << f.val << endl;
}
}
int main()
{
text();
}③结果展示:
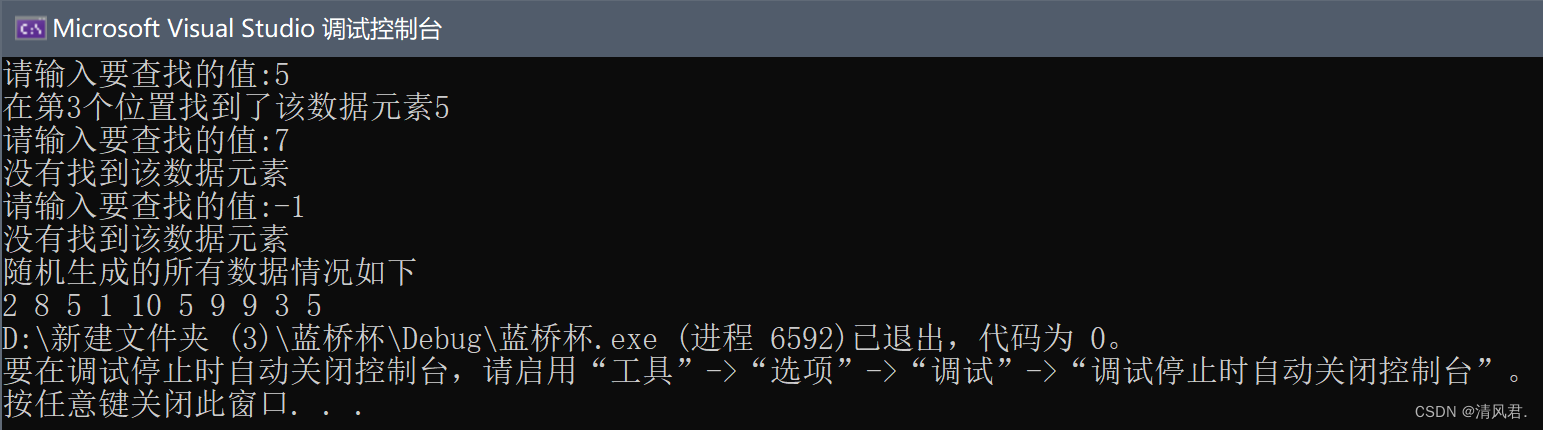
总结
以上就是我们对四类查找算法的分析与学习,查找算法在程序设计问题中经常作为一种重要中间的步骤。比如查找数据后,再对数据进行指定步骤的操作行为,所以要在不同的算法题型中合理地运用查找算法,从而达到最高的效率来解决相应的问题。
<您的三连和关注是我最大的动力>
🚀 文章作者:Keanu Zhang 分类专栏:算法之美(C++系列文章)