基数排序(radix sorting)

实现排序主要是通过关键字之间的比较和移动记录这两种操作来完成的,而实现基数排序不需要进行关键字间的比较,而是利用“分配”和“收集”两种基本操作。

例如,我们可以用分配和收集的方法来对扑克牌进行“排序”
已知扑克牌中 52 张牌面的次序关系为

可以认为,每一张牌有两个“关键字”:

花色

面值

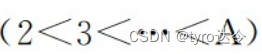
且“花色”的地位高于“面值”。在比较任意两张牌面的大小时,必须先比较“花色”,若“花色”相同则再比较面值。由此,按上述次序关系排列扑克牌时,通常采用的办法是:先按不同“花色“分成有次序的 4 堆,每一堆的牌均具有相同的“花色”,然后分别对每一堆按“面值”大小整理有序。

也可以采用另一种办法:先按不同“面值”分成 13 堆，然后将这 13 堆牌从大到小叠在起(“A”在“K”之上，“K”在“Q”之上·…·最下面的是 4 张“2”),再重新按不同“花色”分成4堆,最后将这 4 堆牌按自小至大的次序合在一起（梅花在最上面，黑桃在最下面）便得到满足式所示的次序关系，如下图所示。

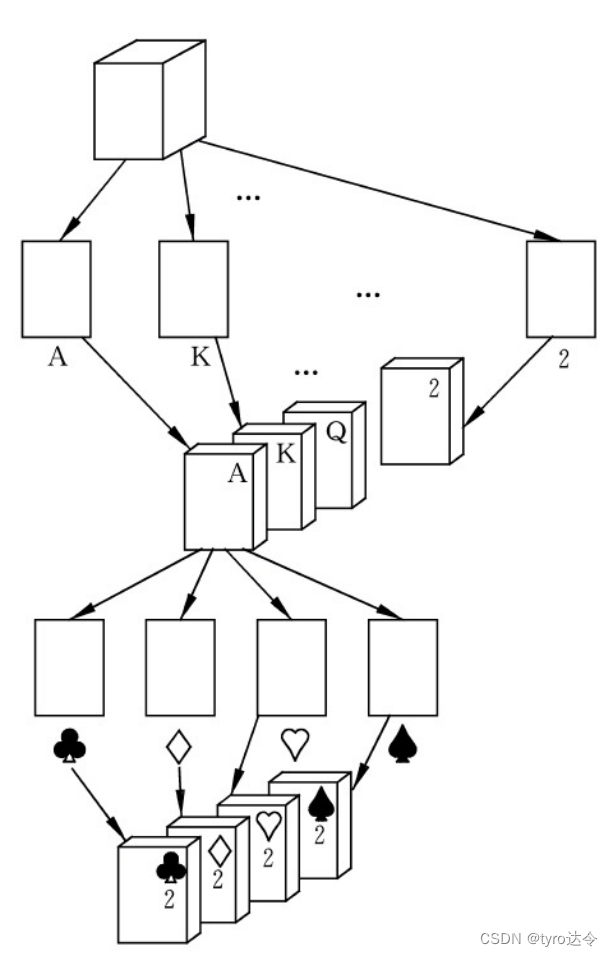
基数排序的思想酷似这种理牌的方法。有的逻辑关键字可以看成由若干个关键字复合而成的。例如,若关键字是数值，且其值都在 O<=k<=999 范围内，则可把每一个十进制数字看成一个关键字，即可认为k由 3 个关键字(k²,k¹,k⁰)组成，其中 k² 是百位数，k¹ 是十位数,k⁰是个位数;又若关键字 k 是由5 个字母组成的单词,则可看成是由 5 个关键字(k⁴,k³,k²,k¹,k⁰)组成,其中每个字母 k^j都是一个关键字,k⁰是最低位, k⁴是最高位。由于如此分解而得的每个关键字 kj都在相同的取值范围内，故可以按分配和收集的方法进行排序。假设记录的逻辑关键字由 d 个“关键字”构成，每个关键字可能取r个值，则只要从最低位关键字起,按关键字的不同值将记录“分配”到 r 个队列之后再“收集”在一起，如此重复 d 趟,最终完成整个记录序列的排序。按这种方法实现的排序称为基数排序，其中“基数”指的是r的取值范围，上述由数字、字母构成的这两种关键字的基数分别为“10”和“26”。

例如,对关键字为(78,09,63,30,74,89,94,25,05,69,18,83)的记录需进行两趟“分配”和“收集”。待排的原始记录如图 3.12(a)所示。第一趟分配对“个位数”进行,根据每个记录关键字个位数的值(0,1,…,9),将它们分配到 10 个队列中去,如图 3.12(b)所示,然后进行第一趟收集,即依个位数为 0,1,…,9 的顺序将记录连接在一起,如图 3.12©所示,之后再按关键字的“十位数”进行分配,分配结果如图 3.12(d)所示,第二趟收集的结果如图 3.12(e)所示,所得即为记录的有序序列。

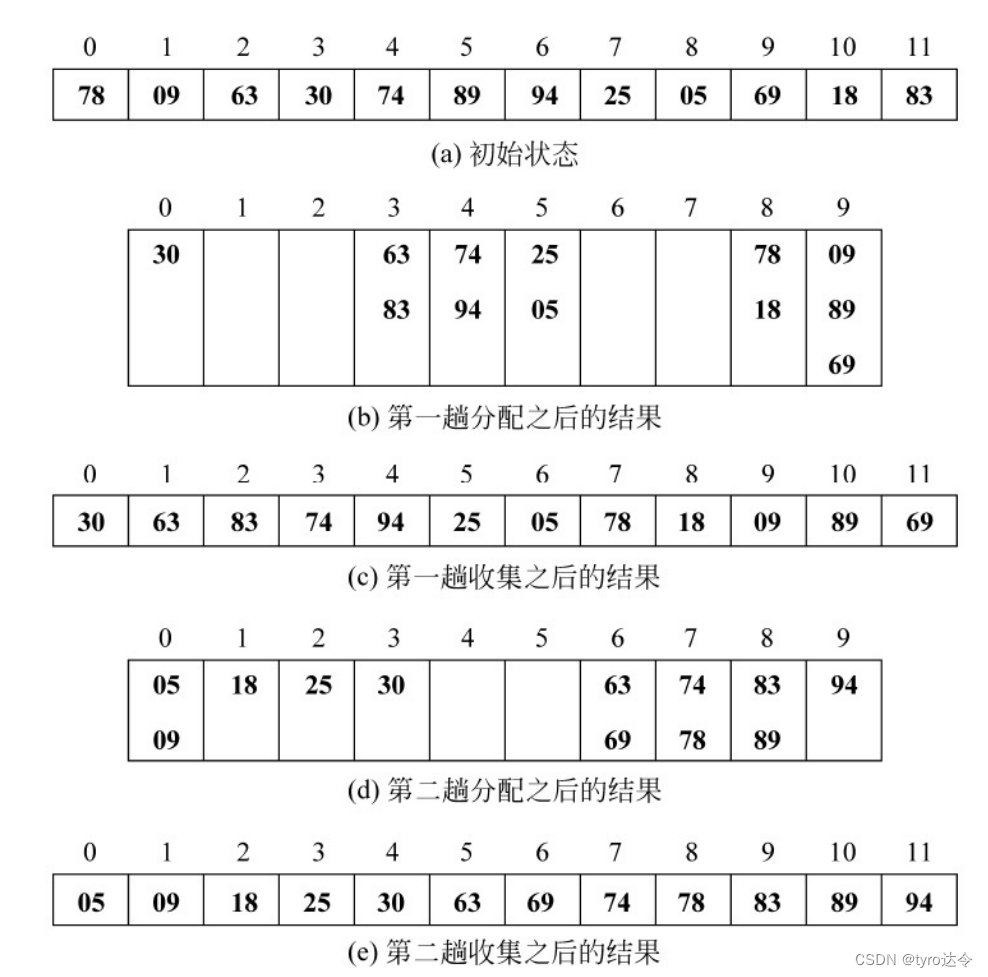
对由顺序表表示法存储的记录进行基数排序可利用“计数”和“复制”的操作实现。分析图 3,12©和图 3,12(a)中记录所在不同位置可见,在©中的第一个记录显然应是对(a)中记录自左至右扫描遇到的第一个个位数最小的记录,关键字为 63 的记录在©中处在第二个位置是因为个位数为“0”、“1”、“2”的记录只有 1个,而由于个位数为“3”的记录有 2 个,则(a)中第一个个位数为“4”的记录在（c）中就应该处在第四个位置上,依此类推。由此可见只要对(a)中记录关键字的“个位数”进行自左至右的扫描计数，便可得到记录在（c）中应处的位置,类似.对（c）中记录关键字的“十位数”进行自左至右的扫描计数,便可得到记录在(e)中应处的位置。从(a)到 （c） 和从（c）到(e)需要一个辅助空间对记录进行“复制”操作，仍以上述关键字为例,利用“计数”和“复制”进行基数排序的过程如下图所示。

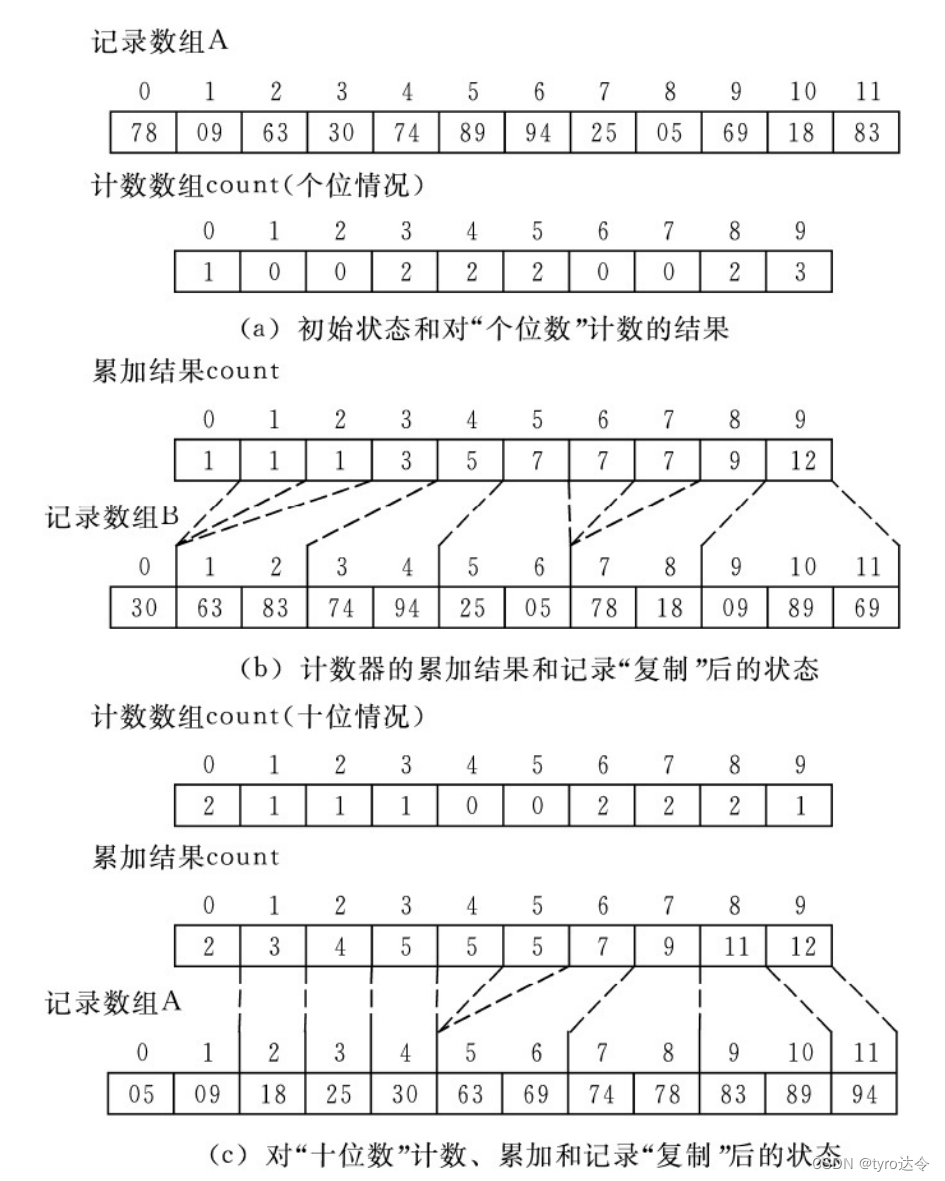
从上图可见,计数数组“累加”(count[i]=count[i]十count[i]=1,…,9) 后的值 count[i]表示记录中关键字该位数取值为“0”至“i”的记录总数，即“原记录数组”中最后一个关键字该位数取值为“i”的记录应该复制到“复制后的数组”中第 count[i]个分量中。例如上图 (b)中,count[5]=7,意味着关键字个位取“0”至“5”的记录共有 7 个。原记录中最后一个关键字个位为 5 的记录 05,复制到“复制后的数组”中第 7 个分量中,位置下标是6;05 前一个个位为 5 的记录 25 的位置下标是 6-1=5。

在描述基数排序的算法之前,尚需重新定义记录类型。

假设记录的逻辑关键字由 d 位数字或字母组成，则需进行 d 躺基数排序,每一趟都要对n个记录进行“计数”和“复制”,则基数排序的时间复杂度为 O(dXn),由于在复制过程中需要和记录数等量的辅助空间,因此它的空间复杂度为 O(n)。