来源：力扣（LeetCode）

描述：

一所学校里有一些班级，每个班级里有一些学生，现在每个班都会进行一场期末考试。给你一个二维数组 classes ，其中 classes[i] = [passi, totali] ，表示你提前知道了第 i 个班级总共有 total_i 个学生，其中只有 pass_i 个学生可以通过考试。

给你一个整数 extraStudents ，表示额外有 extraStudents 个聪明的学生，他们 一定 能通过任何班级的期末考。你需要给这 extraStudents 个学生每人都安排一个班级，使得 所有 班级的 平均 通过率 最大 。

一个班级的 通过率 等于这个班级通过考试的学生人数除以这个班级的总人数。平均通过率 是所有班级的通过率之和除以班级数目。

请你返回在安排这 extraStudents 个学生去对应班级后的 最大 平均通过率。与标准答案误差范围在 10^-5 以内的结果都会视为正确结果。

示例 1：

输入：classes = [[1,2],[3,5],[2,2]], extraStudents = 2
输出：0.78333
解释：你可以将额外的两个学生都安排到第一个班级，平均通过率为 (3/4 + 3/5 + 2/2) / 3 = 0.78333 。

示例 2：

输入：classes = [[2,4],[3,9],[4,5],[2,10]], extraStudents = 4
输出：0.53485

提示：

• 1 <= classes.length <= 10⁵
• classes[i].length == 2
• 1 <= passi <= totali <= 10⁵
• 1 <= extraStudents <= 10⁵

方法：优先队列

思路与算法

由于班级总数不会变化，因此题目所求「最大化平均通过率」等价于「最大化总通过率」。设某个班级的人数为 total，其中通过考试的人数为 pass，那么给这个班级安排一个额外通过考试的学生，其通过率会增加：

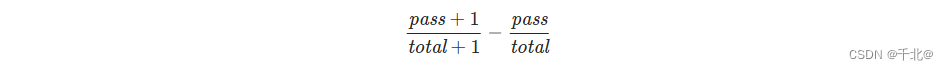
我们会优先选择通过率增加量最大的班级，这样做的正确性在于给同一个班级不断地增加安排的学生数量时，其增加的通过率是单调递减的，即：

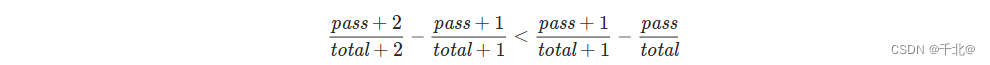
因此当以下条件满足时，班级 j 比班级 i 优先级更大：

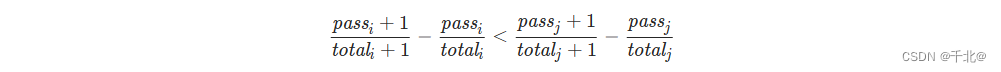
化简后可得：

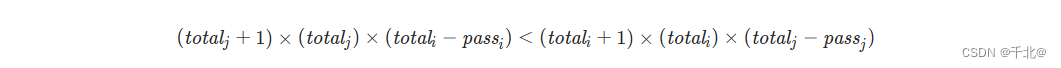
我们按照上述比较规则将每个班级放入优先队列中，进行 extraStudents 次操作。每一次操作，我们取出优先队列的堆顶元素，令其 pass 和 total 分别加 1，然后再放回优先队列。

最后我们遍历优先队列的每一个班级，计算其平均通过率即可得到答案。

代码：

class Solution {
public:
    struct Ratio {
        int pass, total;
        bool operator < (const Ratio& oth) const {
            return (long long) (oth.total + 1) * oth.total * (total - pass) < (long long) (total + 1) * total * (oth.total - oth.pass);
        }
    };

    double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {
        priority_queue<Ratio> q;
        for (auto &c : classes) {
            q.push({c[0], c[1]});
        }

        for (int i = 0; i < extraStudents; i++) {
            auto [pass, total] = q.top();
            q.pop();
            q.push({pass + 1, total + 1});
        }

        double res = 0;
        for (int i = 0; i < classes.size(); i++) {
            auto [pass, total] = q.top();
            q.pop();
            res += 1.0 * pass / total;
        }
        return res / classes.size();
    }
};

执行用时：680 ms, 在所有 C++ 提交中击败了94.29%的用户
内存消耗：85.9 MB, 在所有 C++ 提交中击败了79.05%的用户
复杂度分析
时间复杂度：O((n+m)logn) 或 O(n+mlogn)，其中 n 为classes 的长度，m 等于 extraStudents。每次从优先队列中取出或者放入元素的时间复杂度为 O(logn)，共需操作 O(n+m) 次，故总复杂度为 O((n+m)logn)。堆化写法的时间复杂度为 O(n+mlogn)。
空间复杂度：O(n) 或 O(1)。使用优先队列需要用到 O(n) 的空间，但若直接在 classes 上原地堆化，则可以做到 (1) 额外空间。
author：LeetCode-Solution