算法：（十四）动态规划

文章目录

- 14.1 单序列问题
- - 面试题88：爬楼梯的最少成本
  - 面试题89：偷盗房屋
  - 面试题90:环形偷盗房屋
  - 面试题91：粉刷房子
  - 面试题92：反转字符
  - 面试题93：最长斐波那契数列
  - 面试题94：最少回文分割
- 14.2 双序列问题
- - 面试题95：最长公共子序列
  - 面试题96：字符串交织
  - 面试题97：子序列的数目
- 14.3 矩阵路径问题
- - 面试题98：路径的数目
  - 面试题99：最小路径之和
  - 面试题100：三角形中最小路径之和
- 14.4 背包问题
- - 面试题101：分割等和子集
  - 面试题102：加减的目标值
  - 面试题103：最少硬币数目
  - 面试题104：排列的数目

14.1 单序列问题

面试题88：爬楼梯的最少成本

题目：

数组的每个下标作为一个阶梯，第 i 个阶梯对应着一个非负数的体力花费值 cost[i]（下标从 0 开始）。

每当爬上一个阶梯都要花费对应的体力值，一旦支付了相应的体力值，就可以选择向上爬一个阶梯或者爬两个阶梯。

请找出达到楼层顶部的最低花费。在开始时，你可以选择从下标为 0 或 1 的元素作为初始阶梯。

public int minCostClimbingStairs(int[] cost){
    int[] dp = {cost[0], cost[1]};
    for(int i = 2; i < cost.length; i++){
        dp[i % 2] = Math.min(dp[0], dp[1]) + cost[i];
    }
    return Math.min(dp[0], dp[1]);
}

面试题89：偷盗房屋

题目：

一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响小偷偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组 nums ，请计算不触动警报装置的情况下，一夜之内能够偷窃到的最高金额。

示例：

输入：nums = [1,2,3,1]
输出：4
解释：偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。

面试题90:环形偷盗房屋

题目：一个专业的小偷，计划偷窃一个环形街道上沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都围成一圈，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组 nums ，请计算在不触动警报装置的情况下，今晚能够偷窃到的最高金额。

示例：

输入：nums = [2,3,2]
输出：3
解释：你不能先偷窃 1 号房屋（金额 = 2），然后偷窃 3 号房屋（金额 = 2）, 因为他们是相邻的。

public int rob(int[] values){
    if(values.length == 0){
        return 0;
    }
    if(values.length == 1){
        return values[0];
    }

    int result1 = helper(values, 0, values.length - 2);
    int result2 = helper(values, 1, values.length - 1);
    return Math.max(result1, result2);
}

private int helper(int[] values, int start, int end) {
    int[] dp = {values[0], Math.max(values[0], values[1])};
    for(int i = start + 2; i <= end; i++){
        int j = i - start;
        dp[j % 2] = j % 2 == 0 ? Math.max(dp[0] + values[i], dp[1]) : Math.max(dp[1] + values[i], dp[0]);
    }
    return dp[(end - start) % 2];
}

面试题91：粉刷房子

题目：假如有一排房子，共 n 个，每个房子可以被粉刷成红色、蓝色或者绿色这三种颜色中的一种，你需要粉刷所有的房子并且使其相邻的两个房子颜色不能相同。

当然，因为市场上不同颜色油漆的价格不同，所以房子粉刷成不同颜色的花费成本也是不同的。每个房子粉刷成不同颜色的花费是以一个 n x 3 的正整数矩阵 costs 来表示的。

例如，costs[0][0] 表示第 0 号房子粉刷成红色的成本花费；costs[1][2] 表示第 1 号房子粉刷成绿色的花费，以此类推。

请计算出粉刷完所有房子最少的花费成本。

示例：

输入: costs = [[17,2,17],[16,16,5],[14,3,19]]
输出: 10
解释: 将 0 号房子粉刷成蓝色，1 号房子粉刷成绿色，2 号房子粉刷成蓝色。
最少花费: 2 + 5 + 3 = 10。

public int minCost(int[][] cost){
    if(cost.length == 0){
        return 0;
    }
    int[][] dp = new int[2][3];
    for(int i = 0; i < 3; i++){
        dp[0][i] = cost[0][i];
    }
    for(int i = 1; i < cost.length; i++){
        int j = i % 2;
        dp[j][0] = Math.min(dp[(j + 1) % 2][1], dp[(j + 1) % 2][2]) + cost[i][0];
        dp[j][1] = Math.min(dp[(j + 1) % 2][0], dp[(j + 1) % 2][2]) + cost[i][1];
        dp[j][2] = Math.min(dp[(j + 1) % 2][0], dp[(j + 1) % 2][1]) + cost[i][2];
    }
    int last = (cost.length - 1) % 2;
    return Math.min(Math.min(dp[last][0], dp[last][1]), dp[last][2]);
}

面试题92：反转字符

题目：

如果一个由 ‘0’ 和 ‘1’ 组成的字符串，是以一些 ‘0’（可能没有 ‘0’）后面跟着一些 ‘1’（也可能没有 ‘1’）的形式组成的，那么该字符串是单调递增的。

我们给出一个由字符 ‘0’ 和 ‘1’ 组成的字符串 s，我们可以将任何 ‘0’ 翻转为 ‘1’ 或者将 ‘1’ 翻转为 ‘0’。

返回使 s 单调递增的最小翻转次数。

示例：
输入：s = "00110"
输出：1
解释：我们翻转最后一位得到 00111.

public int minFlipsMonoIncr(String s){
    int[][] dp = new int[2][2];
    dp[0][0] = s.charAt(0) == '0' ? 0 : 1;
    dp[0][1] = s.charAt(0) == '0' ? 1 : 0;
    for (int i = 1; i < s.length(); i++) {
        char c = s.charAt(i);
        int cur = i % 2;
        int pre = (cur + 1) % 2;
        if(c == '0'){
            dp[cur][0] = dp[pre][0];
            dp[cur][1] = Math.min(dp[pre][0], dp[pre][1]) + 1;
        } else if(c == '1'){
            dp[cur][0] = dp[pre][0] + 1;
            dp[cur][1] = Math.min(dp[pre][0], dp[pre][1]);
        }
    }
    return Math.min(dp[(s.length() - 1) % 2][0], dp[(s.length() - 1) % 2][1]);
}

面试题93：最长斐波那契数列

题目：如果序列 X_1, X_2, …, X_n 满足下列条件，就说它是斐波那契式的：

n >= 3

对于所有 i + 2 <= n，都有 X_i + X_{i+1} = X_{i+2}

给定一个严格递增的正整数数组形成序列 arr ，找到 arr 中最长的斐波那契式的子序列的长度。如果一个不存在，返回 0 。

（回想一下，子序列是从原序列 arr 中派生出来的，它从 arr 中删掉任意数量的元素（也可以不删），而不改变其余元素的顺序。例如， [3, 5, 8] 是 [3, 4, 5, 6, 7, 8] 的一个子序列）

示例：

输入: arr = [1,2,3,4,5,6,7,8]
输出: 5
解释: 最长的斐波那契式子序列为 [1,2,3,5,8] 。

public int lenLongestFibSubseq(int[] A){
    int[][] dp = new int[A.length][A.length];
    HashMap<Integer, Integer> map = new HashMap<>();
    for (int i = 0; i < A.length; i++) {
        map.put(A[i], i);
    }
    int result = 0;
    for (int i = 1; i < dp.length; i++) {
        for (int j = 0; j < i; j++) {
            int k  = map.getOrDefault(A[i] - A[j], -1);
            dp[i][j] = k >= 0 && k < j ? dp[j][k] + 1 : 2;
            result = Math.max(result, dp[i][j]);
        }
    }
    return result == 2 ? 0 : result;
}

面试题94：最少回文分割

题目：给定一个字符串 s，请将 s 分割成一些子串，使每个子串都是回文串。

返回符合要求的最少分割次数。

示例：

输入：s = “aab”
输出：1
解释：只需一次分割就可将 s 分割成 [“aa”,“b”] 这样两个回文子串。

public int minCut(String s){
    // 预处理判断s各个子字符串是不是回文字符串
    int length = s.length();
    boolean[][] isPal = new boolean[length][length];
    for (int i = 0; i < length; i++) {
        for (int j = 0; j <= i; j++) {
            char c1 = s.charAt(i);
            char c2 = s.charAt(j);
            if(c1 == c2 && (i <= j + 1 || isPal[j + 1][i - 1])){
                isPal[j][i] = true;
            }
        }
    }

    int[] dp = new int[length];
    dp[0] = 0;
    for(int i = 1; i < length; i++){
        if(isPal[0][i]){
            dp[i] = 0;
        } else {
            dp[i] = i;
            for (int j = 1; j <= i; j++) {
                if(isPal[j][i]){
                    dp[i] = Math.min(dp[i], dp[j - 1] + 1);
                }
            }
        }
    }
    return dp[length - 1];
}

14.2 双序列问题

面试题95：最长公共子序列

题目：

给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。如果不存在公共子序列，返回 0 。

一个字符串的子序列是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如，“ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。
两个字符串的公共子序列是这两个字符串所共同拥有的子序列。

示例：
输入：text1 = "abcde", text2 = "ace" 
输出：3  
解释：最长公共子序列是 "ace" ，它的长度为 3 。

public int longestCommonSubsequence(String s1, String s2){
    int length1 = s1.length();
    int length2 = s2.length();
    if(length1 < length2){
        return longestCommonSubsequence(s2, s1);
    }
    int[] dp = new int[length2 + 1];
    for(int i = 1; i < length1 + 1; i++){
        int prev = 0;
        for(int j = 1; j < length2 + 1; j++){
            int cur;
            if(s1.charAt(i - 1) == s2.charAt(j - 1)){
                cur = prev + 1;
            }else {
                cur = Math.max(dp[j - 1], dp[j]);
            }
            prev = dp[j];
            dp[j] = cur;
        }
    }
    return dp[length2];
}

面试题96：字符串交织

题目：给定三个字符串 s1、s2、s3，请判断 s3 能不能由 s1 和 s2 交织（交错）组成。

两个字符串 s 和 t 交织的定义与过程如下，其中每个字符串都会被分割成若干非空子字符串：

s = s1 + s2 + … + sn
t = t1 + t2 + … + tm
|n - m| <= 1
交织是 s1 + t1 + s2 + t2 + s3 + t3 + … 或者 t1 + s1 + t2 + s2 + t3 + s3 + …
提示：a + b 意味着字符串 a 和 b 连接。

示例 1：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-VwsHE43D-1676748202627)(null)]
输入：s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"
输出：true

public boolean isInterleave(String s1, String s2, String s3){
    if(s1.length() + s2.length() != s3.length()){
        return false;
    }
    int len1 = s1.length();
    int len2 = s2.length();
    if(len1 < len2){
        return isInterleave(s2, s1, s3);
    }
    boolean[][] dp = new boolean[2][len2 + 1];
    dp[0][0] = true;
    for(int j = 1; j < len2 + 1; j++){
        dp[0][j] = s2.charAt(j - 1) == s3.charAt(j - 1) && dp[0][j - 1];
    }

    for(int i = 1; i < len1 + 1; i++){
        dp[i % 2][0] = dp[(i - 1) % 2][0] && s1.charAt(i - 1) == s3.charAt(i - 1);
        for(int j = 1; j < len2 + 1; j++){
            char c1 = s1.charAt(i - 1);
            char c2 = s2.charAt(j - 1);
            char c3 = s3.charAt(i + j - 1);
            dp[i % 2][j] = (dp[(i - 1) % 2][j] && c1 == c3) || (dp[i % 2][j - 1] && c2 == c3);
        }
    }
    return dp[len1 % 2][len2];
}

面试题97：子序列的数目

题目：

给定一个字符串 s 和一个字符串 t ，计算在 s 的子序列中 t 出现的个数。

字符串的一个子序列是指，通过删除一些（也可以不删除）字符且不干扰剩余字符相对位置所组成的新字符串。（例如，“ACE” 是 “ABCDE” 的一个子序列，而 “AEC” 不是）

题目数据保证答案符合 32 位带符号整数范围。

示例 1：

输入：s = “rabbbit”, t = “rabbit”
输出：3
解释：
如下图所示, 有 3 种可以从 s 中得到 “rabbit” 的方案。
rabbbit
rabbbit
rabbbit

public int numDistinct(String s, String t){
    int[] dp = new int[t.length() + 1];
    if(s.length() > 0){
        dp[0] = 1;
    }
    for(int i = 1; i < s.length() + 1; i++){
        int prev = dp[0];
        for(int j = 1; j < t.length() + 1; j++){
            int cur;
            if(s.charAt(i - 1) == t.charAt(j - 1)){
                cur = prev + dp[j];
                prev = dp[j];
                dp[j] = cur;
            } else {
                prev = dp[j];
            }
        }
    }
    return dp[t.length()];
}

14.3 矩阵路径问题

面试题98：路径的数目

题目：

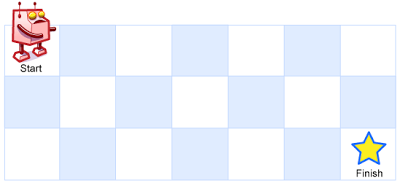
一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例：
输入：m = 3, n = 7
输出：28

public int uniquePaths(int m, int n){
    int dp[] = new int[n];
    Arrays.fill(dp, 1);
    for(int i = 1; i < m; i++){
        for(int j = 1; j < n; j++){
            dp[j] = dp[j] + dp[j - 1];
        }
    }
    return dp[n - 1];
}

面试题99：最小路径之和

题目：给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：一个机器人每次只能向下或者向右移动一步。

示例：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-PGQM00L7-1676748202108)(null)]
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

public int minPathSum(int[][] grid){
    int rLen = grid.length;
    int cLen = grid[0].length;
    int[] dp = new int[cLen];
    dp[0] = grid[0][0];
    for(int j = 1; j < cLen; j++){
        dp[j] = dp[j - 1] + grid[0][j];
    }
    for(int i = 1; i < rLen; i++){
        dp[0] = dp[0] + grid[i][0];
        for(int j = 1; j < cLen; j++){
            dp[j] = Math.min(dp[j - 1], dp[j]) + grid[i][j];
        }
    }
    return dp[cLen- 1];
}

面试题100：三角形中最小路径之和

题目：给定一个三角形 triangle ，找出自顶向下的最小路径和。

每一步只能移动到下一行中相邻的结点上。相邻的结点在这里指的是下标与上一层结点下标相同或者等于上一层结点下标 + 1 的两个结点。也就是说，如果正位于当前行的下标 i ，那么下一步可以移动到下一行的下标 i 或 i + 1 。

示例：

输入：triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
输出：11
解释：如下面简图所示：
2
3 4
6 5 7
4 1 8 3
自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

public int minimumTotal(List<List<Integer>> triangle){
    int[][] dp = new int[2][triangle.get(triangle.size() - 1).size()];
    dp[0][0] = triangle.get(0).get(0);
    for(int i = 1; i < triangle.size(); i++){
        List<Integer> list = triangle.get(i);
        dp[i % 2][0] = dp[(i - 1) % 2][0] + list.get(0);
        dp[i % 2][i] = dp[(i - 1) % 2][i - 1] + list.get(i);
        for(int j = 1; j < list.size() - 1; j++){
            dp[i % 2][j] = Math.min(dp[(i - 1) % 2][j - 1], dp[(i - 1) % 2][j]) + list.get(j);
        }
    }
    int result = Integer.MAX_VALUE;
    for(int i = 0; i < triangle.size(); i++){
        result = Math.min(dp[(triangle.size() - 1) % 2][i], result);
    }
    return result;
}

14.4 背包问题

面试题101：分割等和子集

题目：

给定一个非空的正整数数组 nums ，请判断能否将这些数字分成元素和相等的两部分。

示例：

输入：nums = [1,5,11,5]
输出：true
解释：nums 可以分割成 [1, 5, 5] 和 [11] 。

public boolean canPartition(int[] nums){
    int sum = 0;
    for (int num : nums) {
        sum += num;
    }
    if(sum % 2 == 1){
        return false;
    }
    return subsetSum(nums, sum / 2);
}

public boolean subsetSum(int[] nums, int target){
    boolean[][] dp = new boolean[2][target + 1];
    for(int i = 1; i < nums.length + 1; i++){
        dp[i % 2][0] = true;
        for(int j = 1; j < target + 1; j++){
            dp[i % 2][j] = dp[(i - 1) % 2][j];
            if(!dp[i % 2][j] && j >= nums[i - 1]){
                dp[i % 2][j] = dp[(i - 1) % 2][j - nums[i - 1]];
            }
        }
    }
    return dp[nums.length % 2][target];
}

面试题102：加减的目标值

题目：

给定一个正整数数组 nums 和一个整数 target 。

向数组中的每个整数前添加 ‘+’ 或 ‘-’ ，然后串联起所有整数，可以构造一个表达式：

例如，nums = [2, 1] ，可以在 2 之前添加 ‘+’ ，在 1 之前添加 ‘-’ ，然后串联起来得到表达式 “+2-1” 。
返回可以通过上述方法构造的、运算结果等于 target 的不同表达式的数目。

示例：

输入：nums = [1,1,1,1,1], target = 3
输出：5
解释：一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3

public int findTargetSumWays(int[] nums, int S){
        int sum = 0;
        for (int num : nums) {
            sum += num;
        }
        if(sum < S || (sum + S) % 2 == 1){
            return 0;
        }
        return subsetSum(nums, (sum + S) / 2);
    }

    private int subsetSum(int[] nums, int target) {
        int[][] dp = new int[nums.length + 1][target + 1];
        dp[0][0] = 1;
        for(int i = 1; i < nums.length + 1; i++){
            for(int j = 0; j < target + 1; j++){
                dp[i][j] += dp[i - 1][j];
                if(j >= nums[i - 1]){
                    dp[i][j] += dp[i - 1][j - nums[i - 1]];
                }
            }
        }
        return dp[nums.length][target];
    }

面试题103：最少硬币数目

题目：给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。

你可以认为每种硬币的数量是无限的。

示例：
输入：coins = [1, 2, 5], amount = 11
输出：3 
解释：11 = 5 + 5 + 1

public int coinChange(int[] coins, int target){
    int[][] dp = new int[coins.length + 1][target + 1];
    dp[0][0] = 0;
    for (int i = 1; i < target + 1; i++) {
        dp[0][i] = target + 1;
    }
    for(int i = 1; i < coins.length + 1; i++){
        for(int j = 0; j < target + 1; j++){
            dp[i][j] = dp[i - 1][j];
            for(int k = 1; k * coins[i - 1] <= j; k++){
                dp[i][j] = Math.min(dp[i][j], dp[i - 1][j - k * coins[i - 1]] + k);
            }
        }
    }
    return dp[coins.length][target] > target ? -1 : dp[coins.length][target];
}

面试题104：排列的数目

题目：

给定一个由不同正整数组成的数组 nums ，和一个目标整数 target 。请从 nums 中找出并返回总和为 target 的元素组合的个数。数组中的数字可以在一次排列中出现任意次，但是顺序不同的序列被视作不同的组合。

题目数据保证答案符合 32 位整数范围。

示例：

输入：nums = [1,2,3], target = 4
输出：7
解释：
所有可能的组合为：
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
请注意，顺序不同的序列被视作不同的组合。

public int combinationSum4(int[] nums, int target) {
    int[] dp = new int[target + 1];
    dp[0] = 1;
    for(int i = 0; i < target + 1; i++){
        for (int num : nums) {
            if(i >= num){
                dp[i] += dp[i - num];
            }
        }
    }
    return dp[target];
}