一、本周周赛总结

• T1 模拟。
• T2 脑筋急转弯。
• T3 拆位分析。
• T4 线段树/状压位运算(不是)。

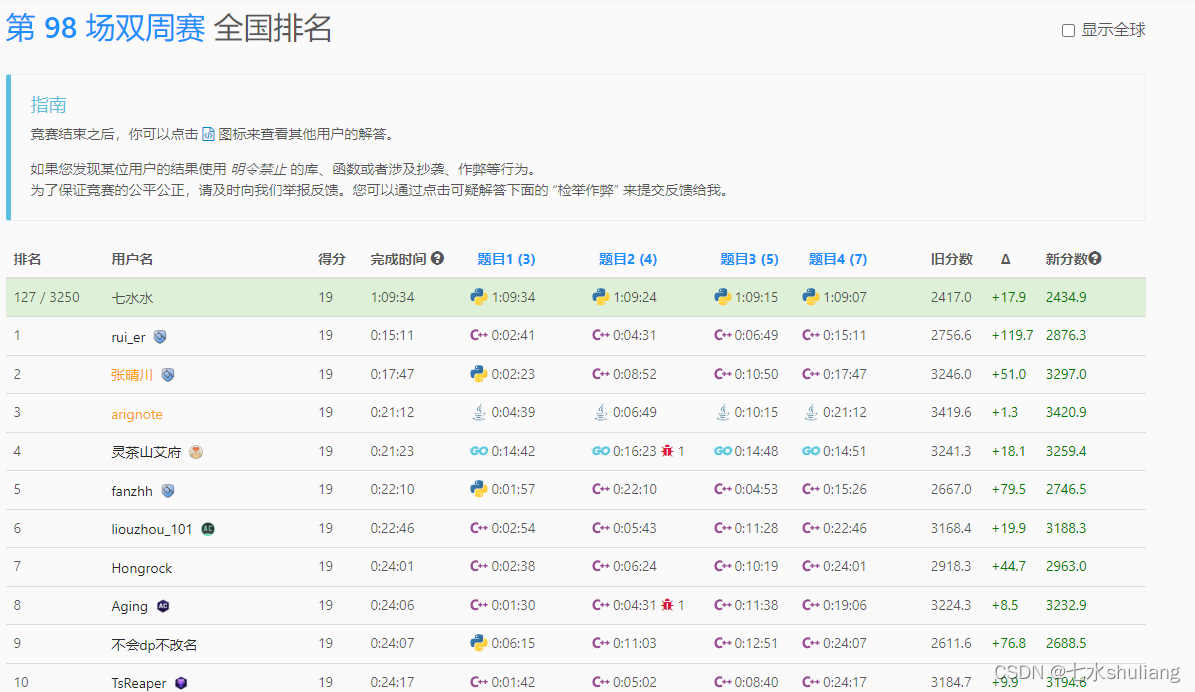
二、 [Easy] 6359. 替换一个数字后的最大差值

链接: 6359. 替换一个数字后的最大差值

1. 题目描述

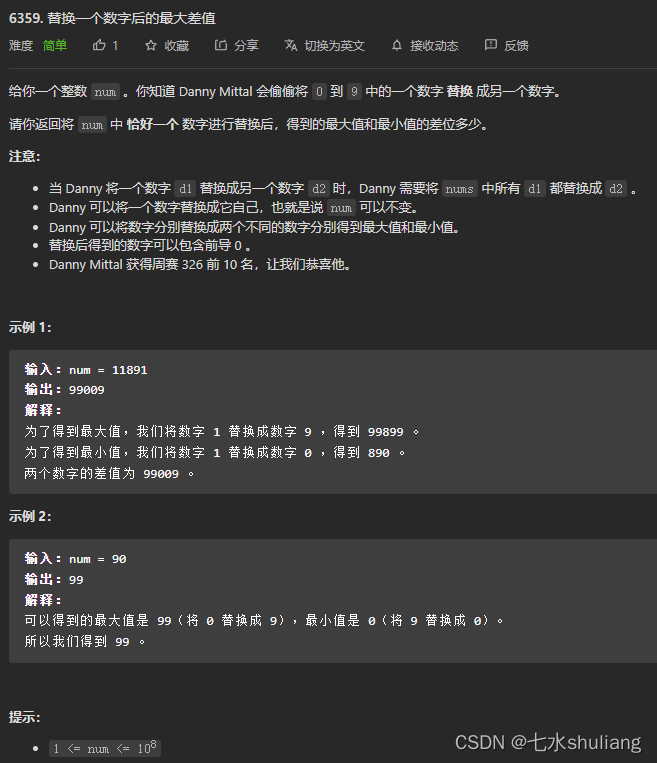
2. 思路分析

• 最小值一定是替换成0得来的。
• 最大值一定是替换成9得来的。
• 无脑暴力模拟。

3. 代码实现

class Solution:
    def minMaxDifference(self, num: int) -> int:
        mx = -inf 
        mn = inf 
        s = str(num)
        for i in range(10):
            p = int(s.replace(str(i),'9'))
            mx = max(mx,p)
            p = int(s.replace(str(i),'0'))
            mn = min(mn,p)
        return mx-mn

三、[Medium] 6361. 修改两个元素的最小分数

链接: 6361. 修改两个元素的最小分数

1. 题目描述

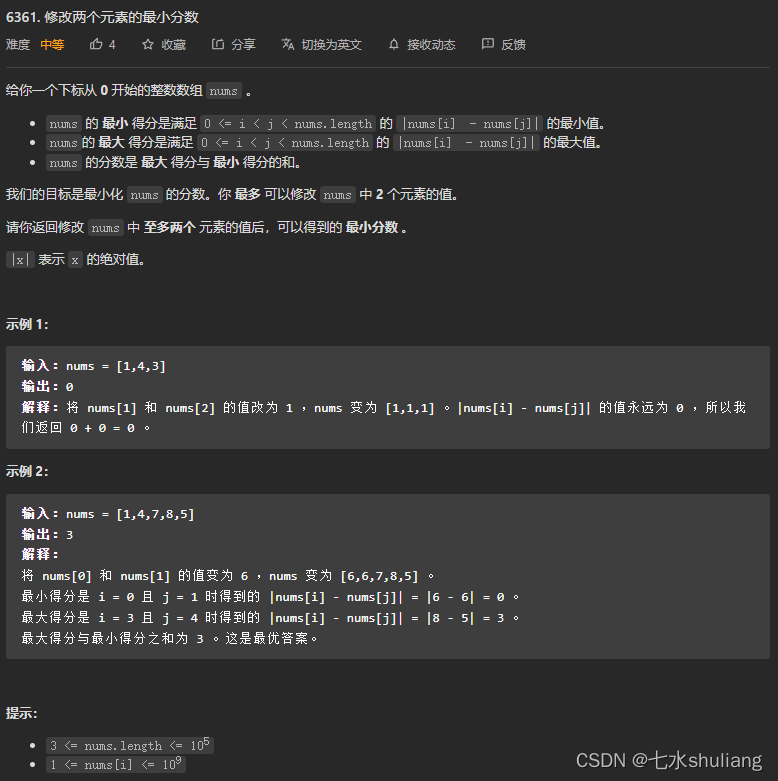
2. 思路分析

脑筋急转弯。

• 修改两个数显然可以相同，最小分一定是0。
• 最终得分就等于最大分。
• 那么缩小最大值和最小值的差即可。
• 即尝试删除两个最小值、删除两个最大值、删除一个最小值一个最大值。

3. 代码实现

class Solution:
    def minimizeSum(self, nums: List[int]) -> int:
        nums.sort()
        return min(nums[-1]-nums[2],nums[-3]-nums[0],nums[-2]-nums[1])

四、[Medium] 6360. 最小无法得到的或值

链接: 6360. 最小无法得到的或值

1. 题目描述

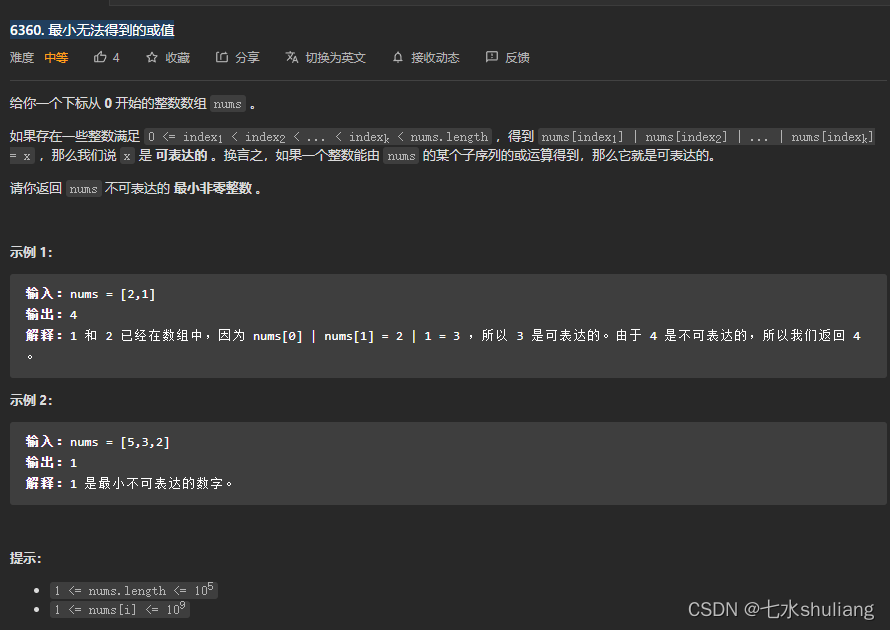
2. 思路分析

• 从小到大考虑每一位为1的情况。
• 比如4 (100)，如果nums中没有4，永远都组合不出来。而4是本位为1的最小值。因此想要4能组合出来，必须4存在于nums。
• 因此可以直接判断所有2的幂存在即可。

3. 代码实现

class Solution:
    def minImpossibleOR(self, nums: List[int]) -> int:
        s = set(nums)
        i = 1
        while i in nums:
            i *= 2
        return i

五、[Hard] 6358. 更新数组后处理求和查询

链接: 6358. 更新数组后处理求和查询

1. 题目描述

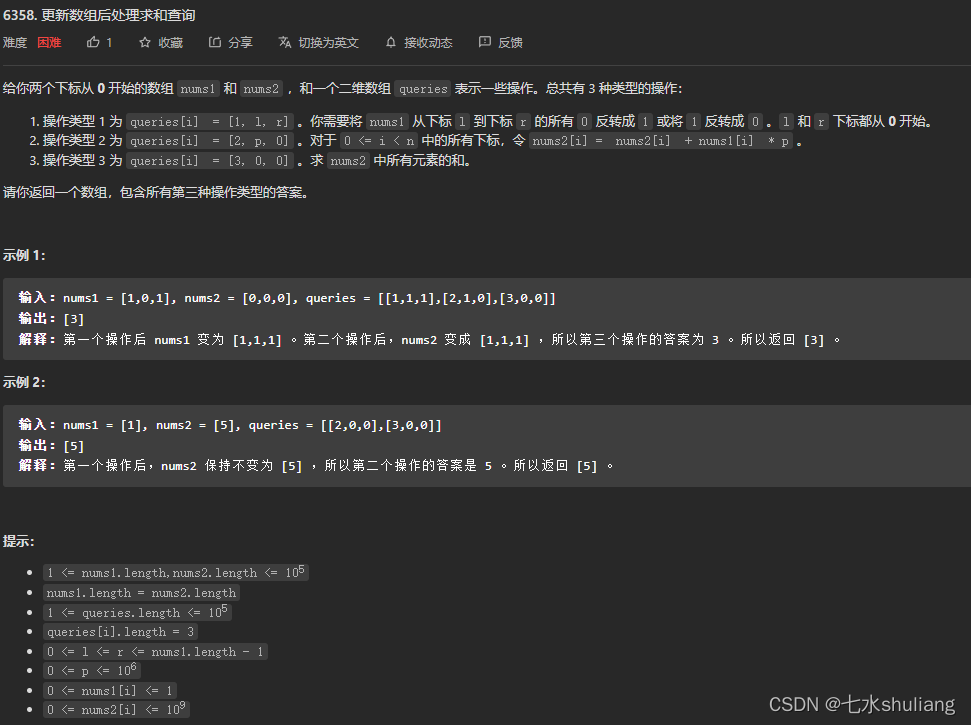
2. 思路分析

复杂度正确的正解是线段树，然而py位运算快更多。

• 题意中操作1是区间更新，直接取反；操作2实际上是查询nums1中含几个1，区间查询。
• 用懒更新RURQ线段树，lazy设置成异或1的变化。
• 注意更新时，线段数的节点值是1的数量取反，即长度-原数量。

---

位运算做法。

• 由于py中的数字是无限位的，那么可以直接把nums1压缩进一个数字，然后用区间异或全1来模拟nums1的变化。
• 用bit_count来计算位1的个数。

3. 代码实现

线段树

class IntervalTree:
    def __init__(self, size):
        self.size = size
        self.interval_tree = [0 for _ in range(size*4)]
        self.lazys = [0 for _ in range(size*4)]

    def give_lay_to_son(self,p,l,r):
        interval_tree = self.interval_tree
        lazys = self.lazys
        if lazys[p] == 0:
            return
        mid = (l+r)//2
        interval_tree[p*2] = mid - l + 1 -  interval_tree[p*2]
        interval_tree[p*2+1] = r - mid - interval_tree[p*2+1]
        lazys[p*2] ^= 1
        lazys[p*2+1] ^=1
        lazys[p] = 0
        
    def update(self,p,l,r,x,y,val):
        """
        把[x,y]区域全变成val
        """
        if y < l or r < x:
            return 
        interval_tree = self.interval_tree    
        lazys = self.lazys        
        if x <= l and r<=y:
            interval_tree[p] = r-l+1-interval_tree[p]
            lazys[p] ^= 1
            return
        self.give_lay_to_son(p,l,r)
        mid = (l+r)//2
        if x <= mid:
            self.update(p*2,l,mid,x,y,val)
        if mid < y:
            self.update(p*2+1,mid+1,r,x,y,val)
        interval_tree[p] = interval_tree[p*2]+ interval_tree[p*2+1]    

    
    def query(self,p,l,r,x,y):
        """
        区间求和      """        
        
        if y < l or r < x:
            return 0
        if x<=l and r<=y:
            return self.interval_tree[p]
        self.give_lay_to_son(p,l,r)
        mid = (l+r)//2
        s = 0
        if x <= mid:
            s += self.query(p*2,l,mid,x,y)
        if mid < y:
            s += self.query(p*2+1,mid+1,r,x,y)
        return s
    
class Solution:
    def handleQuery(self, nums1: List[int], nums2: List[int], queries: List[List[int]]) -> List[int]:
        n = len(nums1)
        s = sum(nums2)
        tree = IntervalTree(n)
        for i,v in enumerate(nums1,start=1):
            if v:
                tree.update(1,1,n,i,i,1)
        ans = []
        for op,l,r in queries:
            if op == 1:
                tree.update(1,1,n,l+1,r+1,1)
            elif op == 2:
                s += l*tree.query(1,1,n,1,n)
            else:
                ans.append(s)
        return ans

位运算

class Solution:
    def handleQuery(self, nums1: List[int], nums2: List[int], queries: List[List[int]]) -> List[int]:
        n = len(nums1)
        s = sum(nums2)
        x = int(''.join(map(str,nums1[::-1])),2)
        
        ans = []
        for op,l,r in queries:
            if op == 1:
                y = (1<<(r-l+1))-1
                y <<= l
                x ^= y
            elif op == 2:
                s += l*x.bit_count()
            else:
                ans.append(s)
        return ans

六、参考链接