一、BFS搜索的原理

• BFS搜索的原理：“逐层扩散”，从起点出发，按层次从近到远，逐层先后搜索。

• 编码：用队列实现。

• 应用：BFS一般用于求最短路径问题，BFS的特点是逐层搜索，先搜到的层离起点更近。

二、BFS：找最短路路径

• 应用场合:点和点直接的距离是1，即边长是1。

寻找从@到*的最短路径。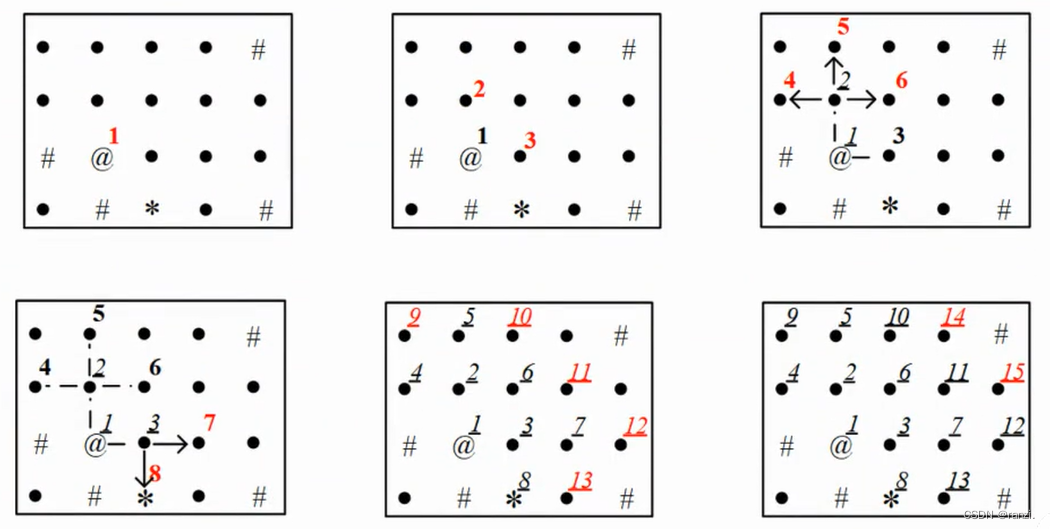

• 使用队列来实现。

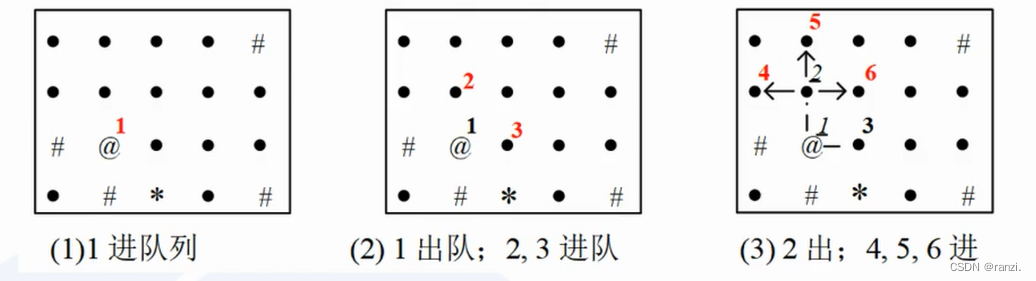
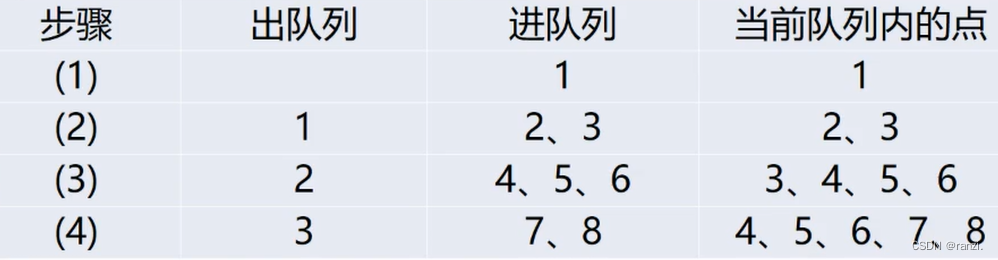
• 最短路径问题用BFS解决（逐层扩散）。

• 往BFS的队列中加入邻居结点时，按距离起点远近的顺序加入: 先加入距离起点为1的邻居结点，加完之后，再加入距离为2的邻居结点，等等。搜完一层，才会继续搜下一层。

三、输出路径的两种方法

• 简单方法：

• 每扩展到一个点v，都在v上存储从起点s到v的完整路径，到达终点t时，便得到了从起点s到t的完整路径。

• 优点：简单、适合小图。

• 缺点：占用大量空间，因为每个点上都存储子完整的路径，不适合大图。

• 标准方法：

• 在每个点上记录它的前驱点，从终点一步步回溯到起点，就可以得到一条完整路径。

• 优点：节省空间，因为每个点上只存储了上一个点，适合大图。

四、蓝桥杯真题(602号)

---

• 题目求字典序最小的最短路径。

• 在每次扩散下一层（往BFS的队列中加入下一层的结点）时，按字典序“D<L<R<U”的顺序加下一层的结点，那么第一个搜到的最短路径就是字典序最小的。

• 计算复杂度：每个点只搜一次，即进入队列和出队列一次。复杂度O(n)，n是迷宫内结点的总数。

• BFS能用于解决1千万个点的最短路问题。

---

• 输出路径的两种方法：

• 简单方法

• 标准方法

路径打印:从终点递归到起点，然后打印

读迷宫代码：

BFS队列实现：

五、连通性判断: BFS

• BFS判断连通性的步骤:

1. 从图上任意一个点u开始遍历，把它放进队列中。

2. 弹出队首u，标记u已搜过，然后搜索u的邻居点，即与u连通的点，放到队列中。

3. 继续弹出队首，标记搜过，然后搜索与它连通的邻居点，放进队列。

4. 继续以上步骤，直到队列为空，此时一个连通块已经找到。其他没有访问到的点，属于另外的连通块，按以上步骤再次处理这些点。

5. 最后所有点都搜到，所有连通块也都找到。

六、BFS的三种实现

• queue

• list

• deque (最快)

用下面的“178号真题”演示三种实现。

七、蓝桥杯真题(178号)

• BFS连通性判断：图论的一个简单问题，给定一张图，图由点和连接点的边组成，要求找到图中互相连通的部分。

---

• 什么岛屿不会被完全淹没?

若岛中有个陆地 (称为高地)，它周围都是陆地，那么这个岛不会被完全淹没。

用BFS搜出有多少个岛 (连通块)，检查这个岛有没有高地，统计那些没有高地的岛(连通块) 的数量，就是答案。

计算复杂度:每个像素点只用搜一次且必须至少搜一次，共N^2个点，BFS的复杂度是O(N^2)，不可能更好了。

---

1.queue

2.list

3.deque

八、BFS判重

• BFS=队列

• BFS：逐步扩展下一层，把扩展出的下一层状态放进队列中处理。

• 如果这些状态有相同的，只需搜一次，只需要进入队列一次。

• 必须判重。

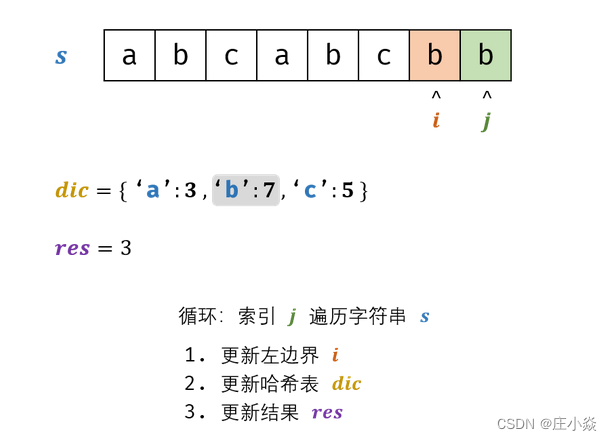
• Python判重方法：字典、set()。

1.字典判重

• 字典：无序、可变、有索引的集合。

• 字典:用花括号定义，有键和值。

2. set判重

• set()函数创建一个无序、不重复元素集

• 关系测试，删除重复数据，计算交集、差集、并集、补集。

九、双向广搜

• 应用场景:有确定的起点s和终点t；把从起点到终点的单向搜索，变换为分别从起点出发和从终点出发的“相遇”问题。

• 操作: 从起点s(正向搜索) 和终点t(逆向搜索) 同时开始搜索，当两个搜索产生相同的一个子状态v时就结束，v是相遇点。得到的s-v-t是一条最佳路径。

• 队列:一般用两个队列分别处理正向BFS和逆向BFS。

• 双向广搜的复杂度

• 当下一层扩展的状态很多时，双向广搜能大大优化，减少大量搜索。

• 由于起点和终点的串不同，正向BFS和逆向BFS扩展的下一层数量也不同，也就是进入2个队列的串的数量不同，先处理较小的队列，可以加快搜索速度。

十、蓝桥杯真题(178号)

---

• 分析：从起始状态到终止状态，求最少跳跃次数，是一个最短路径问题，用BFS。

• 建模：直接让炸蜢跳到空盘有点麻烦，因为有很多在跳。反过来看，让空盘跳，跳到虾蜢的位置，简单多了，只有一个空盘在跳。

• 化圆为线：题目是一个圆圈，不好处理，用一个建模技巧“化圆为线”，把圆形转换为线形。

• 把空盘看成0，有9个数字{0,1,2,3,4,5,6,7,8}，一个圆圈上的9个数字，拉直成了一条线上的9个数字，这条线的首尾两个数字处理成相连的。

• 八数码问题：有9个数字{0,1,2,3,4,5,6,7,8}，共有9!=362880种排列，不算多。

• 最短路径：

• 初始状态:“012345678”,目标状态:“087654321”。

• 从初始状态“012345678”跳一次，有4种情况:“102345678”、“210345678”“812345670”、“712345608”。

• 然后从这4种状态继续跳到下一种状态，一直跳到目标状态为止。

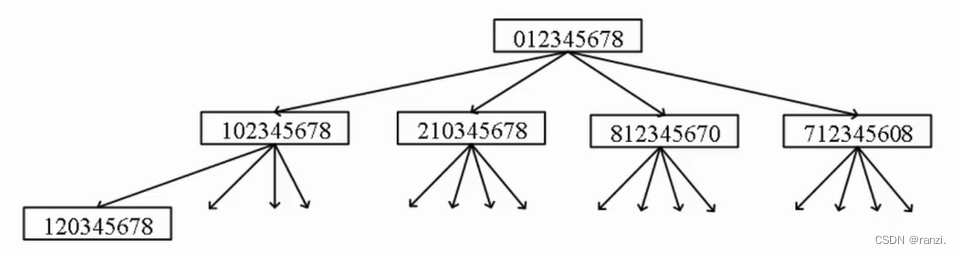
• 用BFS扩展每一层。

• 每一层就是炸蜢跳了一次，扩展到某一层时发现终点“087654321”，这一层的深度就是蛇蟠跳跃的次数。

• 为什么去重?

• 如果不去重：第1步到第2步，有4种跳法;第2步到第3步，有4*4种;...;第20步，有4^20 =1万亿种，那可就完犊子了。

• 判断有没有重复跳，如果跳到一个曾经出现过的情况，就不用往下跳了。一共只有9!=362880种情况。

• 代码复杂度

• 在每一层，能扩展出最少4种、最多362880种情况，最后算出的答案是20层，那么最多算20*362880=7257600次。在代码中统计实际的计算次数，是1451452次。

• 队列:最多有9!=362880种情况进入队列。

---

1. 字典去重，用list实现队列，速度慢:3s

2. set()去重，用list实现队列，速度快:1.4s

3.双向广搜

队列q1 : 正向搜索

队列q2 : 逆向搜索

• 用cnt统计运行了多少次:54568次。

• 前面用普通BFS计算:1451452次。

• 双向广搜的计算量只有4%。