Leetcode - 503

这题其实和下一个更大元素那题一样，只是说可以找自己前面的元素，那我索性就把遍历范围从本序列延长到两个相同序列。这样某个元素寻找下一个更大元素到本序列末尾后还可以继续往下，也就是从序列头开始找。

这里依旧是可以用单调栈装元素下标，若遍历到一个比栈顶元素（下标）对应的元素更大的元素，那么出栈，将这个值赋值给结果数组的下标对应位置。这里的单调栈可以设置为nums长度的两倍，这样赋值时候更方便，也可以长度和nums一致，这样赋值的时候，我们可以对出栈元素（下标）取模(%len(nums))这样可以。 另外出栈是一个循环过程，只要栈不为空和栈顶元素小于新元素时就一直出栈。最后让新元素入栈。

def nextGreaterElements(self, nums: List[int]) -> List[int]:
        nums = nums + nums

        stack = []
        res = [-1] *2 *  len(nums)

        for i,v in enumerate(nums):
            if stack:
                while stack and v > stack[-1][1]:
                    out = stack.pop()
                    res[out[0]] = v

                stack.append([i,v])
            else:
                stack.append([i,v])

        return res[:len(nums)//2]

Leetcode - 42

本地是重点题，掌握两种解法。

1. 双指针法，其实也不是双指针，只是一种思想。首先首尾元素不计算，因为左右两侧不存在围墙。

其次，注意计算方向，像这种方法里，我们只用计算竖向方向，所以每个位置都是单独计算的，计算方法为，当前位置，左侧最高处，和右侧最高处的最小的那个，减去自己位置的高度，就得出了当前位置能储水的最高高度，宽度为1。所以面积就是1*最高高度

def trap(self, height: List[int]) -> int:
        res = 0
        for i in range(len(height)):
            if i == 0 or i == len(height)-1: continue
            lHight = max(height[:i])
            rHight = max(height[i+1:])
            
            res1 = min(lHight,rHight) - height[i]        
            if res1 > 0:
                res += res1
        return res

2. 单调栈法：和前面一样，从栈顶到栈底的元素顺序是从小到大的。 这种方法处理水槽的方向是横向的，所以不用一个位置一个位置地处理。当当前高度大于栈顶元素对应高度，就开始计算面积，此时意味着“夹”出了槽，此时高度和宽度都是需要计算的，还需要用到栈顶的前一个元素，作为左壁，

高度就是当前元素 的高度 和左壁的高度的最小值再减去栈顶元素对应高度。

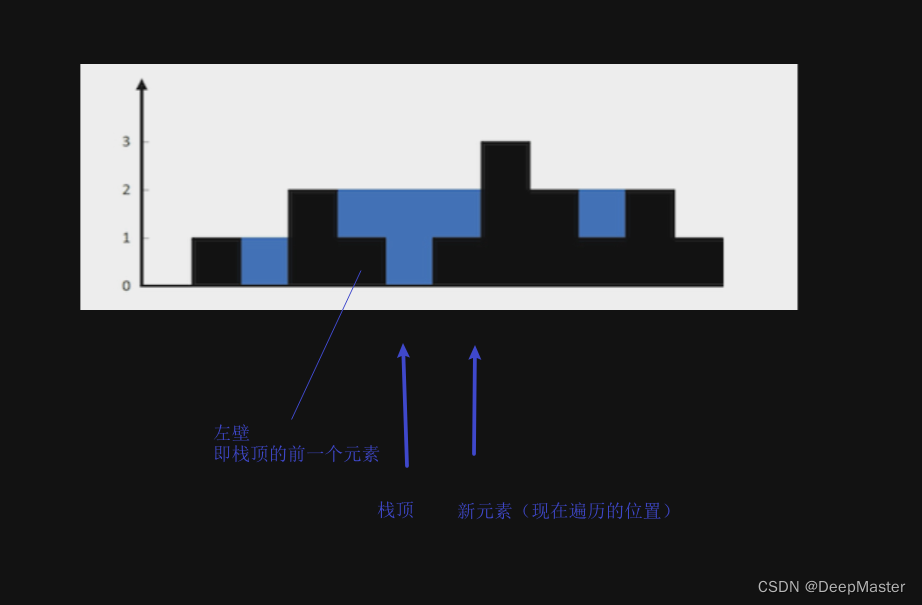
如图，碰到新元素之前，单调栈里的元素对应的高度依次是（2，1，0），现在碰到元素高度为1，所以要开始计算了。

水槽高度就为 min(1, 1) -0 = 1

宽度为新元素下标减去左壁下标再减去一，如图设左壁下标为0，元素就是2，夹出来的水槽的宽度刚好是 （2- 1） -1 = 1 ，所以此时水槽宽度是1，面积是 1 * 1 = 1.

此时0出栈，栈顶是1，但是新元素也是1，此时需要替换掉原来高度相同的那个元素，换成新元素对应的下标并入栈。

再往后 碰到一个更大的了，高度3，

此时根据左壁位置和新元素位置，宽度就是3，如图。

高度就是新元素和左壁的最小值再减去栈顶元素高度 min(3,2) - 1 = 1. 水槽面积是 3 * 1 = 3合理

def trap(self, height: List[int]) -> int:
        res = 0
        stack = []

        stack.append(0)

        for i,v in enumerate(height):
            if i ==0:
                continue
            temp = height[stack[-1]]
            if v < temp:
                stack.append(i)
            
            elif v == temp:
                stack.pop()
                stack.append(i)

            else:
                while stack and v > height[stack[-1]]:
                    # 栈顶就是中间的柱子：储水槽，就是凹槽的地步
                    mid_height = height[stack[-1]]
                    stack.pop()
                    if stack:
                
                        left_height = height[stack[-1]]
                        # 两侧的较矮一方的高度 - 凹槽底部高度
                        h = min(v, left_height) - mid_height
                        # 凹槽右侧下标 - 凹槽左侧下标 - 1: 只求中间宽度
                        w = i - stack[-1] - 1
                        # 体积：高乘宽
                        res += h * w
                stack.append(i)

        return res