数据分析spss应急考试
前言
-
单项选择 15(项)*2(分)=30
判断题 10*1 = 10
计算题 2*10
-
案例分析题目(考实验内容) 总四十分,分值不等
- 老师重点强调了
- 回归分析
- 因子分析
- 方差分析
- 参数、非参数检验
- 2独立样本的非参数检验应该用什么方法
- 多独立样本的应该用什么方法
- 配对样本的应该用什么方法
- 买会?,vr?,中位数……适用于那些数据
- 抽样
- 给你一个案例,你可不可以写出抽样思路
- 先是整群还是先是分层
- 简单随机抽样
- 给你一个案例,你可不可以写出抽样思路
-
spss的logistic回归不考
-
判别分析不考
-
spss的线性回归分析中的曲线分析也不考
软件分析
- 你的spss的格式 它能读那些的 考一些选择判断
相关分析
- 相关分析它的一个范围, 多少是正相关、多少是负相关,当相关系数是0的时候表示没有线性相关性质
聚类分析、因子分析是案例分析的重点
第四章补充讲了抽样
spss软件概述
利用spss进行数据分析一般经过:
建立数据文件、加工整理数据、分析数据、解释分析结果四个阶段
spss运行方式菜单式进行操作
spss数据文件建立和管理
spss的数据文件是一个有结构的,包含了变量视图和数据视图
唯一标识变量的是变量名
变量名标签
- 是对变量名做一个解释说明
变量值标签
- 对变量所取值的一些解释说明,增强分析结果的 可视性
比如在年纪录入时:用 1 表示 大一年纪、用2表示大二年纪
计量尺度(Measurement)
-
数值型(定距)
-
定序型(有固有大小或高低顺序)
-
定类型(无固有大小或高低顺序,分类)
变量测量包含了标度测量、有序测量与名义测量三种
其中标度测量对应定量变量,有序测量对应定序,名义测量对应定类变量。
数据的录入
一行就是一个个案
读取文本格式数据文件有读取固定格式和自由格式两种,自由格式必须要有分隔符
spss数据的保存
spss 数据默认后缀 .sav
spss结果文件默认后缀是 .spv
读取其他格式的数据文件
.sav .zsav .sys .port .bdf .dat .txt .csv
不能读.ppt
数据文件的合并
* 恒向合并
* 纵向合并
* 按照关键字关键字的升序排序合并用 横向合并
数据预处理
数据的排序
排序的目的是找到数据中最大值&最小值,进而计算数据的全距和离散程度
排序分为:单值排序 多重排序
- 那些属于定量变量
- 数值型的比如:年龄、合格率、身高、工资
- 那些属于定性变量
- 比如:专业、性别、职称
个案排秩和变量排序作用是不一样的
想知道某一个观测在已知条件下观测的位置,而又不希望打破数据现有的排序,可以用个案排秩
变量的计算
——通过现有变量得到新的变量
变量计算是针对所有个案的,每个个案都有自己的计算结果。
重新编码为相同的变量
重新编码为不同的变量
为了某个数据只在一个组中出现一次、编码和分区 都有一个区间
数据选取的基本方式
1. 选取全部数据
2. 按指定条件选取
3. 随机抽样:(近似抽样、精确抽样)
* 精确抽样:用户给定两个参数:希望选取的个案数、在前几个个案中选择
4. 选取某区域样本
* 选取指定范围内的所有个案,适用于 **时间序列**
5. 使用过滤个案,对**使用过滤个案,是对缺失值进行一个过滤**
对于计数的数据分析要进行加权的处理
统计学依据数据的计量尺度将数据分成三类**:定量、定序、定类**
两大类:定量(定距、定比)、定性(定序、定类)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-6CpO4Uzl-1676652396847)(C:\Users\Admin\AppData\Roaming\Typora\typora-user-images\image-20230216165430276.png)]](https://img-blog.csdnimg.cn/760b57024d37461e9f49a27864caaa7c.png)
行列互换是数据的转置
spss基本统计分析
刻画度量集中趋势的有
* **均值**
* **中位数**
* **众数**
集中趋势:数据想中心值靠拢的程度
刻画离散趋势有
- 标准差
- 极差
- 方差
离散趋势:数据远离中心值的程度
度量分布形态有
- 偏度
- 于正态分布而言 小于0 左偏,大于 0 右偏
- 分度
- 大于0 (有时候和3做出比较、看公式中有无做减3的处理)比正太分布陡峭,小于 0 比正态分布要平缓
分布形态:描述数据陡峭程度、是否对称等
频数分析
——用图标的形式对数据做一个简单的描述
频数:是指变量落在某个区域的次数
频数分析中出现的图表有哪些:条形图、饼图、直方图(可以通过直方图看,分布是否呈现正态分布)
- 条形图适用于–定序、定类变量分析
- 饼图,研究占比
- 直方图,适用于–定距型变量分析
变量的计算尺度
定类(比如表示性别):只能计次
定序(一件产品的满意度,如果用1表示非常满意,2表示比较满意,3表示中等满意,4表示比较不满意,5表示非常不满意):计次、排序
定距(比如温度之类的):计次、排序、加减
定比(体重):计次、排序、加减、乘除
下列哪些选项是不属于频数分析中统计量的 卡方
- 百分位数
- 集中趋势
- 离散趋势
- 分布形态
- 卡方
交叉分组下的频数分析
——针对多变量
当我们要研究变量 ≥ 2 \geq 2 ≥2个变量时使用交叉分组
边缘分布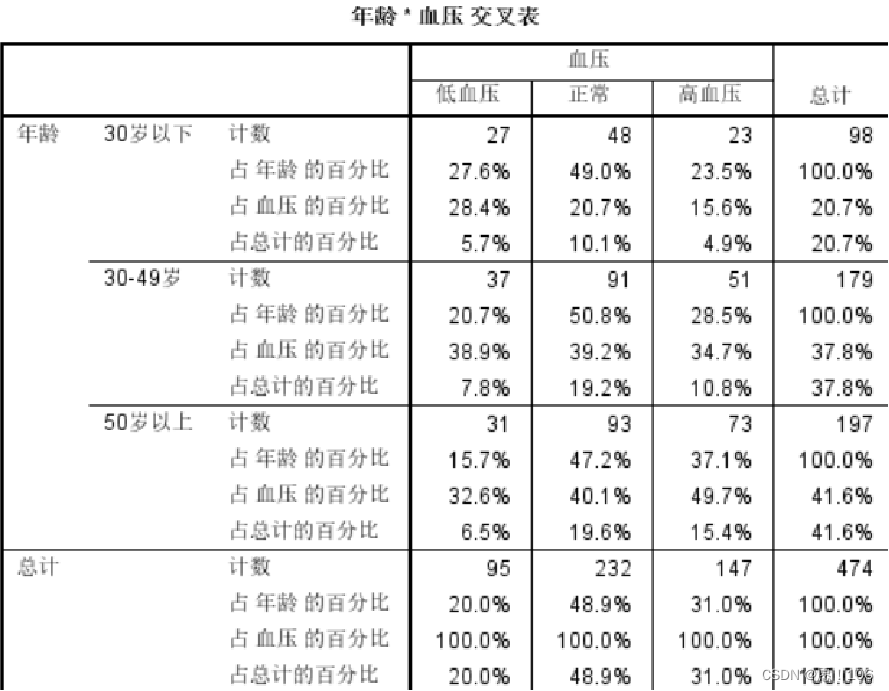
上表中的年龄变量称为行变量(Row),血压称为列变量(Column)。行标题和列标题分别是两个变量的变量值(或分组值)。表格中间是观测频数和各种百分比。
474人中,低血压、正常、高血压的人数分别为95、232、147,构成的分布称为交叉列联表的列边缘分布;
30岁以下、30-49岁、50岁以上的人数分别为98、179、197,构成的分布称为交叉列联表的行边缘分布;
98个低血压的人中各年龄段的人数分别是27,37,31,这些频数构成的分布称为条件分布,即在行变量(列变量)取值条件下的列变量(行变量)的分布。
交叉连表的卡方检验
步骤:
- 建立原假设
- 假设行变量与列变量独立
- 选择和计算检验统计量
- 计算观测值和临界值
- 结论和决策
- 利用卡方统计量的这个值和临界值进行比较
- 观测值 > > >临界值,实际分布与期望分布过大拒绝原假设
- <,反之同意
卡方统计量观测值的大小取决于两个因素:第一:列联表的单元格子数;第二:观测频数与期望频数的总差值。
多选项分析
对应于多选项分析之前要进行分解,分解有 多选项二分法(变量取值 0 or 1 )和多选项分类法(对于多选项问题可以选几个答案)
抽样
应该会考一道分析题:
多阶段抽样(重要、一定要理解各种抽样意义)
要做这道题你首先要理解不同抽样的意义:
概率抽样
-
简单随机抽样:从总体N个单位中随机地抽取n个单位作为样本 ,每个单位入抽样本的概率是相等的
-
分层抽样:将抽样单位按某种特征或某种规则划分为 不同的层,然后从不同的层中独立、随机 地抽取样本
-
整群抽样:将总体中若干个单位合并为组(群),抽样时 直接抽取群,然后对中选群中的所有单位全部实施调查
- 例子:一个年纪 1000人,要抽样500个人他们的数学成绩进行调查
将1000人分为20个班
因此我们只需选出10个班进行调查
- 例子:一个年纪 1000人,要抽样500个人他们的数学成绩进行调查
-
系统抽样:.将总体中的所有单位(抽样单位)按一定顺 序排列,在规定的范围内随机地抽取一个 单位作为初始单位,然后按事先规定好的 规则确定其它样本单位
- 先从数字1到k之间随机抽取一个数字r作为 初始单位,以后依次取r+k,r+2k…等单位
例题




抽样分布
正态分布和均值、标准差有关
三大分布-和自由度有关
- X 2 \mathcal{X}^2 X2分布
- f f f分布
- t t t分布
中心极限定理
设从均值为 μ \mu μ,方差为 σ 2 \sigma^2 σ2的一个任意总 体中抽取容量为n的样本,当n充分大时,样本均值的抽样分布近似服从均值为 μ \mu μ、方差为 σ 2 / n \sigma^2/n σ2/n的正态分布
对于方差和均值(重要)

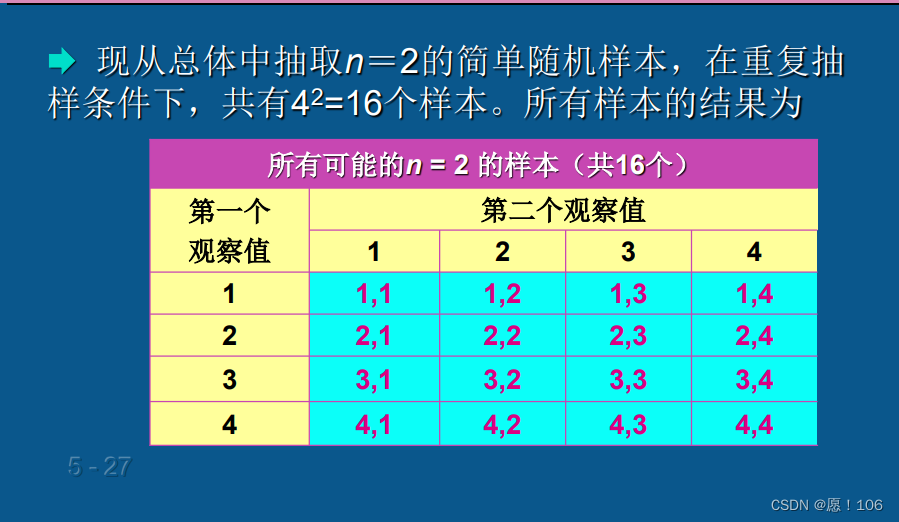
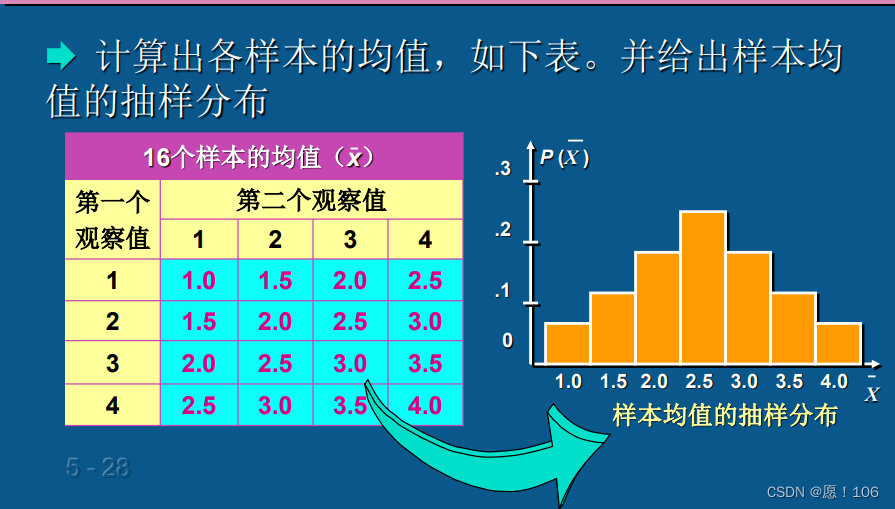
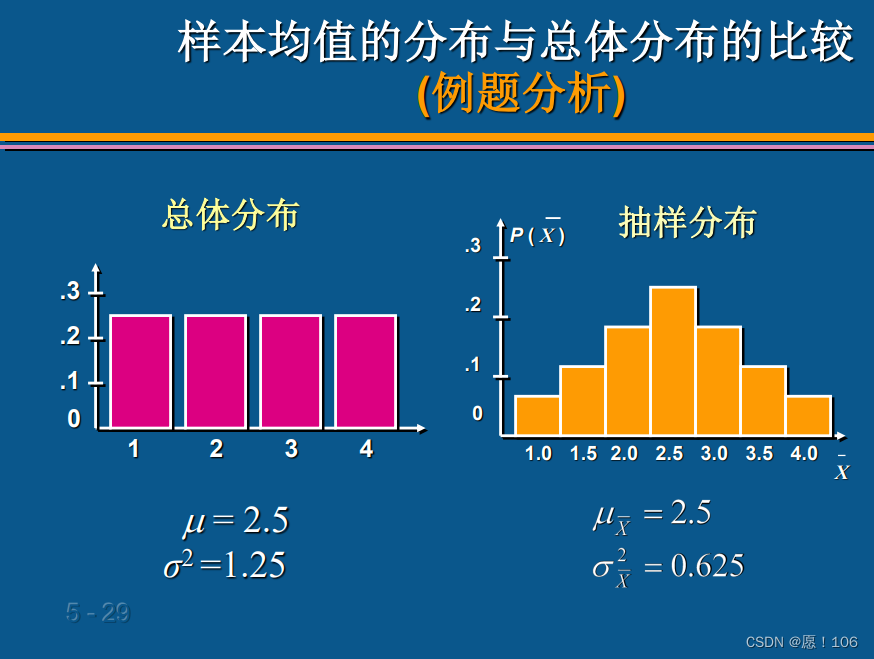
标准差就是方差开根号
卡方分布(服从行-1*列-1的自由度)、t分布、f分布是和自由度有关的
正态分布和自由度是无关的
判断数据是否是正态分布用 p-p图(概率-概率图) Q-Q图(分位数-分位数图),带有正态曲线的直方图去看
正态分布分成三类我们利用严格意义上的正态分布(通过KS、KW检验),近似正态(KS、KW检验的没有通过、但没有严重的偏态)
参数检验
假设检验
步骤
-
确定 h 0 h_0 h0 假设和备择假设$ h_1$
- 单样本t检验:验一个样本平均数与一个已知的总体平均数的差异是否显著, h 0 h_0 h0不显著, h 1 h_1 h1相反
- 两个独立样本t检验:检验两个样本平均数与其各自所代表的总体的差异是否显著, h 0 h_0 h0不显著, h 1 h_1 h1相反
- 两个配对样本t检验:可视为单样本t检验的扩展,不过检验的对象由一群来自常态分配独立样本更改为二群配对样本之观测值之差
-
选择检验统计量、在 h0条件下确定检验统计量的分布
- 使用t检验,就假设服从t分布
- 算出概率值,选取显著性水平 α \alpha α
-
如果概率值和a进行比较 概率值 > α \alpha α,不拒绝h0,概率值< α \alpha α,拒绝
假设检验中的两类错误
- 第一类(弃真错误)
- 原假设为真时拒绝原假设
- 第一类错误的概率为 α \alpha α(显著性水平)
- 第二类错误(取伪错误)
- 原假设为假时接受原假设
- 第二类错误的概率为 β \beta β
单样本t检验:数据总体要近似服从正态分布
两独立样本t检验:数据总体要近似服从正态分布 + 两个样本相互独立
两配对样本t检验:数据总体要近似服从正态分布 + 两个配对样本
比如:你要求减肥茶有没有用你要得到
- 喝减肥茶之前的样本和减肥茶之后的样本
方差分析
方差分析是一个假设参数检验的范畴,是研究是均值的差异,它有两个前提:样本的总体正态或近似正态、各总体的方差应该相同
方差分析研究的并不是方差,而是均值的变异,即推断多个总体的均数是否有差别。它是一个多独立样本检验
不管是单因素还是多因素,它其实研究的是一个或多个控制变量对一个观测变量的一个影响(我们的观测变量只有一个)
观测变量 是一个连续性的数值性变量
这个控制变量是一个分类型的变量
(我们把不同的分类称之为不同的水平)
单因素,多因素、协方差分析它选择的统计量是什么F统计量
检验统计量:总变差=组间差异+组内差异
| 总平方和 | 自由度 | 均方 | F | ||
|---|---|---|---|---|---|
| 组间 | A | k-1 | A/(k-1) | ( A / ( k − 1 ) ) ÷ B / ( n − k ) (A/(k-1)) \div B/(n-k) (A/(k−1))÷B/(n−k) | |
| 组内 | B | n(总的个案数)-k | B/(n-k) | 无 | |
| 总计 | A+B | n-1 | 无 | 无 |
进行决策如果F的概率P > α \alpha α,说明控制变量在不同水平下对观测变量不产生了显著影响,概率值< α \alpha α,说明控制变量在不同情况下产生了显著影响
非参数检验
肯定会考案例分析
参数检验 V S VS VS 非参数检验
异
| 参数检验 | 非参数检验 |
|---|---|
| 数据总体要近似服从正态分布 | 所有数据都可以用 |
| 灵敏度更高 | 灵敏度比参数检验低 |
| 参数检验要利用到总体的信息(总体分布、总体的一些参数特征如方差),以总体分布和样本信息对总体参数作出推断 | 非参数检验不需要利用总体的信息(总体分布、总体的一些参数特征如方差),以样本信息对总体分布作出推断。 |
同
都是统计分析方法的重要组成部分
单样本非参数检验
二项检验 用来检验是否符合二项分布 适用于离散型变量,要求检验变量必须为数值型的二元变量。
卡方检验 用来检验总分布和已知分布是否有显著差异 适用于分类变量的统计推断
K-S检验 推断总体是否服从某个理论分布 适用于探索连续随机变量的分布情况
变量值的随机性检验 利用样布数据对总体可能出现的随机值进行检验
以上都用于单样本非参数
两独立样本非参数检验
-
曼-惠特尼U检验(Mann-Whitney U):平均秩检验
- 大样本、小样本情况如何分析
-
k-s检验
-
游程检验(Wald-Wolfowitz runs)
多独立样本非参数检验
- 中位数检验
两配对样本非参数检验
- 变化显著性检验(McNemar)
- 符号检验
- 符号平均秩检验(wilcoxon)
多配对样本非参数检验
- Friedman检验
理解多独立样本、两配对样本和多配对样本非参数检验方法的设计思想,重点掌握K-W检验方法、Wilcon符号秩检验和Friedman检验的基本原理及使用场合,熟练掌握数据组织方式和具体操作
理解SPSS单样本非参数检验方法的设计思想,重点掌握卡方检验和K-S检验的基本原理和计算过程,并熟练掌握其具体操作
非常有可能是是计算题



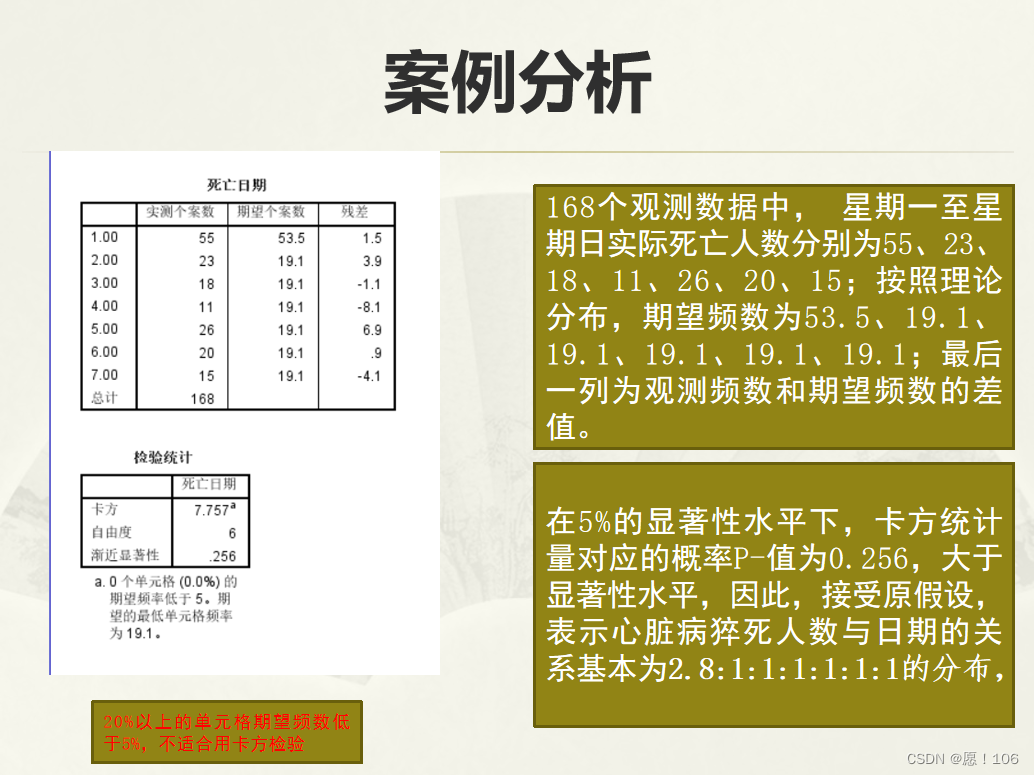


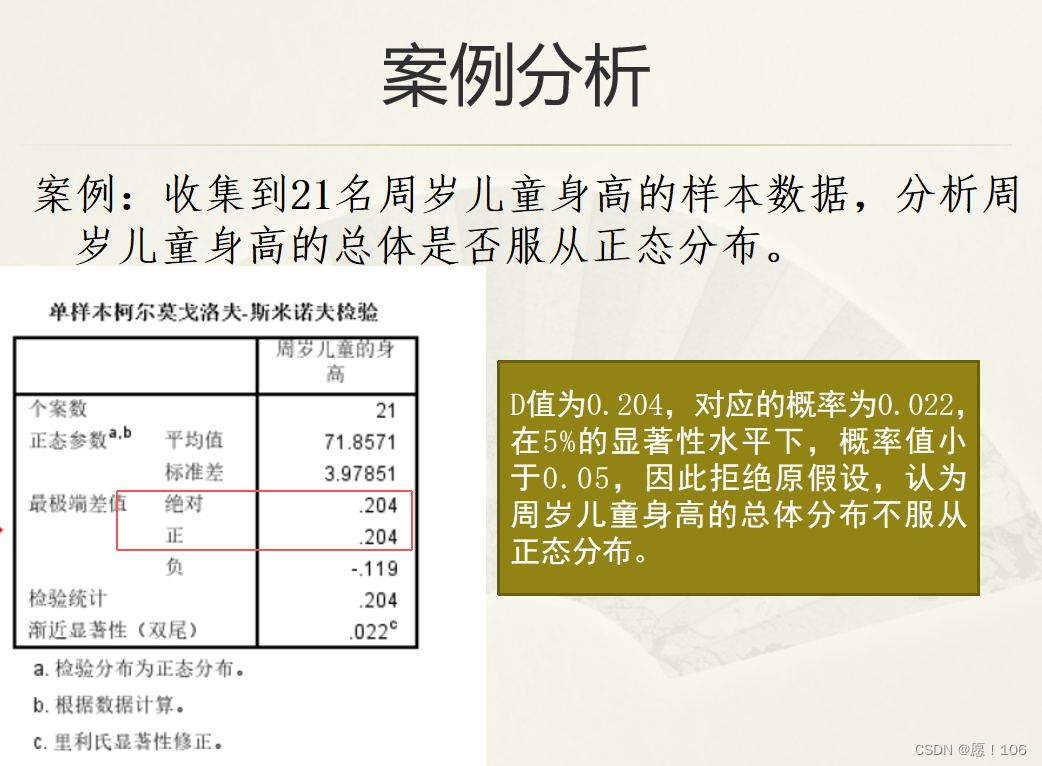
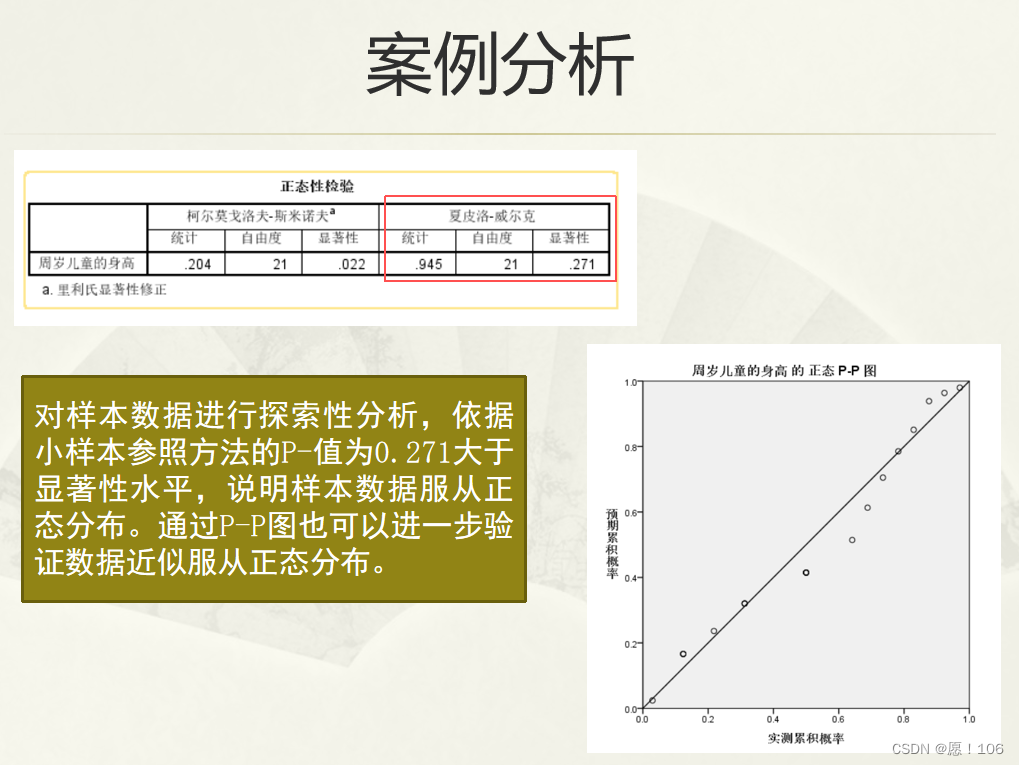
相关分析
相关变量间的关系一般分为两种:平行关系、因果关系。统计学上采用相关分析研究呈平行关系的相关变量之间的关系。
散点图有正相关和负相关
相关系数有:Spearman相关系数(计算数值型)、Kendall相关系数(计算分类型)、简单线性相关系数(Pearson)(计算分类型)
相关系数越接近1正相关性越强、越接近-1负相关性越强、等于0无线无线性相关。但也有可能有其他的关系,有曲线的等等。
因子分析
判断适不适合因子分析:
-
相关系数矩阵中相关系数>0.3
-
KMO >0.6
-
巴特利特球形检验:给出的原假设是这个相关系数矩阵,它是一个单位阵
提取因子,提取的是否有效。看你的这个因子能不能解释原有变量的大部分变差,若干个因子提取的较为合理,最终因子和因子之间的这个相关系数矩阵应该是一个单位值。
也就是说两个因子之间相关系数是为零的,就不相关。
聚类分析
聚类分析无监督、无先验知识
层次聚类(系统聚类)
一种是R型、针对个案
一种是Q型、针对变量
把变量做一个聚类,就是一个降维
spss默认距离是组间平局连锁距离;最短距离、最近距离关键看有木有加上类中个体与个体之间的距离
层次聚类中可以形成形成一个范围内的解,但是K均值聚类一旦K确定就只能聚成K类
spss的判别分析
Fisher判别法、贝叶斯判别法用于分类、有先验知识、有监督
![[MySQL]初识数据库](https://img-blog.csdnimg.cn/img_convert/ddc48061334f9d94dacbb94df155a73c.gif)