蒙特卡洛方法

理解：是一种利用大量样本与样本中正确数量形成的概率去逼近真实值的一种方法。

可以很巧妙的求取某些问题：如 π 的值

1、利用蒙特卡洛方法求π

我们知道圆的面积公式是：π * r * r

那么 1 / 4 圆的面积就是 1/ 4 *π * r * r

此时我们有这么一个边长为 1 的正方形、又有一个半径为 1 的圆，让 1 / 4 的圆放在这个正方形中：如下图

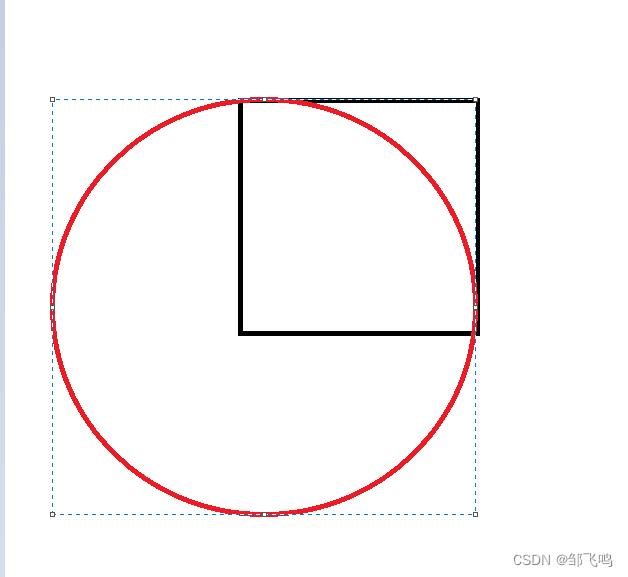
然后、此时我们随机的在正方形区域打点：

我们可以知道、点可能落在圆内，也可能在圆外、那么当打点次数足够多时，是完全有可能将正方形每一个地方都打点、那么在正方形中 1 / 4 圆的面积就应该是：正方形的面积 * 点打在圆内的概率。

也就是说 ：

​ 1 / 4 圆的面积 = 正方形的面积 * 打在圆内点数量 / 全部点数量

即：（假设圆半径、正方形边长都为 1、打在圆内点数量为 count_y 、总点数为 ： count ）

​ 1/ 4 *π * 1 * 1 = 1 * 1 * count_y / count

简化为：

​ π = 4 * count_y / count

即：我们只需要求出点打在圆内的概率就能知道 π 的值。

那么：怎么知道点是打在圆内呢？

通过 点 到 圆心的长度与圆半径比较即可。

且 点打的越多、概率越逼近此正方形内 1/4圆 与 正方形 面积的比值，即真实的π值

上代码！

from random import random

# 假设正方形边长、圆半径都为1、
countall = 10000000 # 总点数
count_y = 0 # 在圆内点数

for i in range(countall):
    x = random() # 因为此随机数范围正好在 0~1，符合正方形边长、所以获取的 x，y就相当于在正方形中随机的一个点
    y = random()
    # 判断这个点在不在圆内
    if pow((x * x + y * y), 0.5) < 1:
        count_y += 1

print("当点数为："+str(countall)+" 时、π值为："+str(4 * count_y / countall))

结果：
当点数为 100 时、π值为：3.16
当点数为：10000 时、π值为：3.1164
当点数为：1000000 时、π值为：3.143912
当点数为：10000000 时、π值为：3.1412768
当点数为：100000000 时、π值为：3.14212396

可以看到、当次数足够多时、最后计算 π 的值是越逼近真实值的、但是既然是概率作为驱动、所以每一次的值不可能一样、甚至可能出现次数太多反而没那么精确（可能是次数还不够、但是一亿次啊喂、再多电脑就跑太久了）

最后：不只是可以用来计算 π ，比如说一张不规则图片、分 白。黑两色、求白色面积、此时依旧可以使用此方法判断落点处颜色与整体落点数进而求面积