最大的以 1 为边界的正方形【LC1139】

给你一个由若干 0 和 1 组成的二维网格 grid，请你找出边界全部由 1 组成的最大 正方形 子网格，并返回该子网格中的元素数量。如果不存在，则返回 0。

写了50分钟写出来了 思路是对的 但就是不够清晰 并且想着先写再说 然后越写越有点乱 感觉是个坏习惯 以后还是得想清楚了再写 不然好浪费时间呐

写出来了还是心满意足的 java时间2ms 100%

• 思路：

  • 使用前缀和数组记录每个位置向左和向上连续1的个数，记为$rows[i][j]$和$cols[i][j]$

  • 然后使用变量a记录当前成立的正方形的最大边长，枚举正方形的每个右上顶点$(i,j)$，其向左连续1的个数为$rows[i][j]$，当该正方形的边长大于$a$时才会对结果有影响，因此当$rows[i][j]>a$时，枚举该正方形可能的边长$b \in (a,rows[i][j]] $，判断该正方形是否合法。

  • 该正方形的四个顶点如下图所示，如果B顶点向上连续1的个数和向左连续1的个数大于等于b，并且C顶点向上连续1的个数大于等于b，那么该正方形成立

    

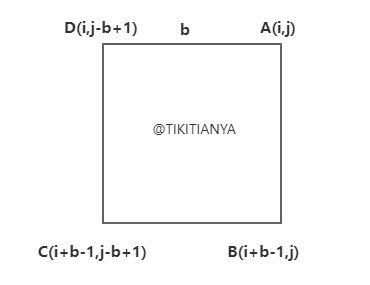
• 实现

  class Solution {
      public int largest1BorderedSquare(int[][] grid) {
          int n = grid.length;
          int m = grid[0].length;
          int[][] rows = new int[n + 1][m + 1];
          int[][] cols = new int[n + 1][m + 1];
          for (int i = 0; i < n; i++){
              for (int j = 0; j < m; j++){
                  if (grid[i][j] == 1){
                      rows[i + 1][j + 1] = rows[i + 1][j] + 1;
                  }                
              }
          }
          for (int i = 0; i < m; i++){
              for (int j = 0; j < n; j++){
                  if (grid[j][i] == 1){
                      cols[j + 1][i + 1] = cols[j][i + 1] + 1;
                  }                
              }
          }
          int a = 0;// 边长
          for (int i = 1; i <= n ; i++){
              for (int j = 1; j <= m ; j++){
                  for (int b = rows[i][j]; b > a; b--){
                      if (b > a && i + b - 1 <= n 
                          && rows[i + b - 1][j] >= b 
                          && cols[i + b - 1][j - b + 1] >= b 
                          && cols[i + b - 1][j] >= b){
                          a = b;
                          break;
                      }
                  }
                  
              }
          }
          return a * a;
  
      }
  }
  

  • 复杂度
    • 时间复杂度：$O(n^2)$
    • 空间复杂度：$O(n^2)$