相关链接:
- 【路径分割】序列分隔和路径提取的案例
- 【算法】LNS(大邻域算法)和ALNS(自适应大邻域算法)(持更)
- Python实现(MD)VRPTW常见求解算法——自适应大邻域搜索算法(ALNS),本文也是该篇的解析
- 干货 | 自适应大邻域搜索(Adaptive Large Neighborhood Search)入门到精通超详细解析-概念篇
- 自适应大邻域搜索(Adaptive Large Neighborhood Search)-详解
- 自适应大邻域 | 用ALNS框架求解一个TSP问题 - 代码详解
文章目录
- 0. 简介
- 一、Destory
- 1.1 随机破坏
- 1.2 最坏值破坏
- 1. 3 执行破坏算子
- 二、Repair
- 2.1 随机修改
- 2.2 贪婪修复
- 搜索贪婪修复位置
- 2.3 最大贡献值修复
- 搜索最大贡献值
- 2.4 执行修复算子
- 三。选择--破坏and修复的类型
- 更新算子权重
- 重置得分
0. 简介
ALNS是从LNS发展扩展而来的,在了解了LNS以后,我们现在来看看ALNS。ALNS在LSN的基础上,允许在同一个搜索中使用多个destroy和repair方法来获得当前解的邻域。
ALNS会为每个destroy和repair方法分配一个权重,通过该权重从而控制每个destroy和repair方法在搜索期间使用的频率。 在搜索的过程中,ALNS会对各个destroy和repair方法的权重进行动态调整,以便获得更好的邻域和解。简单点解释,ALNS和LNS不同的是,ALNS通过使用多种destroy和repair方法,然后再根据这些destroy和repair方法生成的解的质量,选择那些表现好的destroy和repair方法,再次生成邻域进行搜索。
solution的邻域
一个解x经过destroy和repair方法以后,实则是相当于经过了一个邻域动作的变换.

上图是三个CVRP问题的解,上左表示的是当前解,上右则是经过了destroy方法以后的解(移除了6个customers),下面表示由上右的解经过repair方法以后最终形成的解(重新插入了一些customers)。
上面展示的只是生成邻域中一个解的过程而已,实际整个邻域还有很多其他可能的解。比如在一个CVRP问题中,将destroy方法定义为:移除当前解x中15%的customers。假如当前的解x中有100名customers,那么就有C(100,15)= 100!/(15!×85!) =2.5×10的17次方 种移除的方式。并且,根据每一种移除方式,又可以有很多种修复的方法。这样下来,一对destroy和repair方法能生成非常多的邻居解,而这些邻居解的集合,就是邻域了.
destroy和repair的形象

伪代码

代码的主要函数
# 数据结构:解
class Sol()
# 数据结构:需求节点
Class Node()
# 数据结构:车场节点
Class Depot()
# 数据结构:全局参数
Class Model()
# 读取csv文件
Def readCSVFile()
# 初始化参数:计算’距离矩阵、时间矩阵、初始信息素’
Def calDistanceTimeMatrix()
# 计算路径费用
Def calTravelCost()
# 根据Split结果,提取路径
Def splitRoutes()
# 计算目标函数
Def calObj()
# 随机构造初始解
Def genInitialSol()
# 随机破坏
Def createRandomDestory()
# 最值破坏
Def crateWorseDestory()
# 随机修复
Def createRandomRepair()
# 贪婪修复
Def createGreadyRepair()
# 搜索贪婪修复位置
Def findGreedyInsert()
# 最大贡献值修复
Def createRegretRepair()
# 搜索最大贡献值
Def find RegretInsert()
# 选择修复破坏算子
Def selectDestoryRepair()
# 执行破坏算子
Def doDestory()
# 执行修复算子
Def doRepair()
# 重置得分
Def resetScore()
# 更新算子权重
def updateWeight()
# 绘制目标函数收敛曲线
Def plotObj()
# 输出优化结果
Def outPut()
# 绘制优化车辆路径,以3个车场为例
Def plotRoutes()
# 运行函数
Def run()
一、Destory
1.1 随机破坏
def createRandomDestory(model):
d=random.uniform(model.rand_d_min,model.rand_d_max)
reomve_list=random.sample(range(model.number_of_demands),int(d*(model.number_of_demands-1)))
return reomve_list
- model.rand_d_max = 0.4 # 随机破坏最大破坏比例
- model.rand_d_min = 0.1 # 随机破坏最小破坏比例
- model.number_of_demands=len(model.demand_id_list)需求节点数目
int(d*(model.number_of_demands-1):破坏的节点个数
- return :破坏的节点(们)的ID
1.2 最坏值破坏
def createWorseDestory(model,sol):
deta_f=[]
for node_no in sol.node_no_seq:
node_no_seq_=copy.deepcopy(sol.node_no_seq)
node_no_seq_.remove(node_no)
obj,_,_,_=calObj(node_no_seq_,model)
deta_f.append(sol.obj-obj)
sorted_id = sorted(range(len(deta_f)), key=lambda k: deta_f[k], reverse=True)
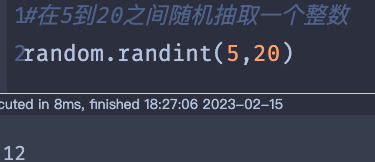
d=random.randint(model.worst_d_min,model.worst_d_max)
remove_list=sorted_id[:d]
return remove_list
- sol.node_no_seq: sol的整数型基因编码
- sol.obj:sol的目标值
- model.worst_d_min = 5 # 最坏值破坏最少破坏数量
- model.worst_d_max = 20 # 最坏值破坏最多破坏数量
- sorted_id:是根据(破坏后的解的)obj值从小到大排序所对应的node_id号。

- return :破坏的节点(们)的ID
1. 3 执行破坏算子
def doDestory(destory_id,model,sol):
if destory_id==0:
reomve_list=createRandomDestory(model)
else:
reomve_list=createWorseDestory(model,sol)
return reomve_list
- destory_id: 0-1随机数,用来选择执行 随机破坏还是最值破坏
- 随机破坏:随机破坏几个节点
- 最值破坏:根据某个解sol,破坏obj值降低最大的几个节点
二、Repair
2.1 随机修改
def createRandomRepair(remove_list,model,sol):
unassigned_node_no_seq=[]
assigned_node_no_seq = []
# remove node from current solution
for i in range(model.number_of_demands):
if i in remove_list:
unassigned_node_no_seq.append(sol.node_no_seq[i])
else:
assigned_node_no_seq.append(sol.node_no_seq[i])
# insert
for node_no in unassigned_node_no_seq:
index=random.randint(0,len(assigned_node_no_seq)-1)
assigned_node_no_seq.insert(index,node_no)
new_sol=Sol()
new_sol.node_no_seq=copy.deepcopy(assigned_node_no_seq)
new_sol.obj,new_sol.route_list,new_sol.route_distance,new_sol.timetable_list=calObj(assigned_node_no_seq,model)
return new_sol
- 按照node_no_seq的顺序,将节点分为未分配节点和已分配节点
- unassigned_node_no_seq:未分配节点序列
- assigned_node_no_seq:已分配节点序列
- 将未分配节点 依次插入,插入位置的索引随机生成。
- 以新的node_no_seq生成一个new_sol,并计算new_sol的属性
- 返回new_sol
2.2 贪婪修复
def createGreedyRepair(remove_list,model,sol):
unassigned_node_no_seq = []
assigned_node_no_seq = []
# remove node from current solution
for i in range(model.number_of_demands):
if i in remove_list:
unassigned_node_no_seq.append(sol.node_no_seq[i])
else:
assigned_node_no_seq.append(sol.node_no_seq[i])
#insert
while len(unassigned_node_no_seq)>0:
insert_node_no,insert_index=findGreedyInsert(unassigned_node_no_seq,assigned_node_no_seq,model)
assigned_node_no_seq.insert(insert_index,insert_node_no)
unassigned_node_no_seq.remove(insert_node_no)
new_sol=Sol()
new_sol.node_no_seq=copy.deepcopy(assigned_node_no_seq)
new_sol.obj,new_sol.route_list,new_sol.route_distance,new_sol.timetable_list=calObj(assigned_node_no_seq,model)
return new_sol
- 按照node_no_seq的顺序,将节点分为未分配节点和已分配节点
- unassigned_node_no_seq:未分配节点序列
- assigned_node_no_seq:已分配节点序列
-
while :未分配的节点
- 使用
findGreedyInsert获得插入的节点insert_node_no和索引insert_index - assigned_node_no_seq,按照索引插入节点
- unassigned_node_no_seq删除当前节点
- 使用
-
以新的node_no_seq生成一个new_sol,并计算new_sol的属性
-
返回new_sol
搜索贪婪修复位置
def findGreedyInsert(unassigned_node_no_seq,assigned_node_no_seq,model):
best_insert_node_no=None
best_insert_index = None
best_insert_cost = float('inf')
assigned_obj,_,_,_=calObj(assigned_node_no_seq,model)
for node_no in unassigned_node_no_seq:
for i in range(len(assigned_node_no_seq)):
assigned_node_no_seq_ = copy.deepcopy(assigned_node_no_seq)
assigned_node_no_seq_.insert(i, node_no)
obj_, _,_,_ = calObj(assigned_node_no_seq_, model)
deta_f = obj_ - assigned_obj
if deta_f<best_insert_cost:
best_insert_index=i
best_insert_node_no=node_no
best_insert_cost=deta_f
return best_insert_node_no,best_insert_index
- best_insert_node_no=None ,从unassigned_node_no_seq选择最佳插入的节点
- best_insert_index = None,插入节点的最佳位置
- best_insert_cost = float(‘inf’),插入的成本
- assigned_obj: assigned_node_no_seq(部分节点序列)的目标值
一. 对于未分配的节点进行循环,循环次数为:未分配的节点个数
1. 对于插入的位置进行循环,循环次数为:未分配的节点个数+1
1) assigned_node_no_seq_:已分配节点序列的 ’深复制‘
2) 按照循环的索引位置,将节点插入
3)计算新序列 assigned_node_no_seq_的obj值
4)deta_f: 目标值的增幅
5) 判断:增幅值是否小于当前记录的最大插入成本
a. 更新 最佳插入索引best_insert_index
b. 更新最佳插入节点best_insert_node_no
c. 更新最大插入成本best_insert_cost
二、return :最佳插入节点和最佳索引
2.3 最大贡献值修复
def createRegretRepair(remove_list,model,sol):
unassigned_node_no_seq = []
assigned_node_no_seq = []
# remove node from current solution
for i in range(model.number_of_demands):
if i in remove_list:
unassigned_node_no_seq.append(sol.node_no_seq[i])
else:
assigned_node_no_seq.append(sol.node_no_seq[i])
# insert
while len(unassigned_node_no_seq)>0:
insert_node_no,insert_index=findRegretInsert(unassigned_node_no_seq,assigned_node_no_seq,model)
assigned_node_no_seq.insert(insert_index,insert_node_no)
unassigned_node_no_seq.remove(insert_node_no)
new_sol = Sol()
new_sol.node_no_seq = copy.deepcopy(assigned_node_no_seq)
new_sol.obj, new_sol.route_list,new_sol.route_distance,new_sol.timetable_list = calObj(assigned_node_no_seq, model)
return new_sol
- 按照node_no_seq的顺序,将节点分为未分配节点和已分配节点
- unassigned_node_no_seq:未分配节点序列
- assigned_node_no_seq:已分配节点序列
-
while :未分配的节点
- 使用
findRegretInsert获得插入的节点insert_node_no和索引insert_index - assigned_node_no_seq,按照索引插入节点
- unassigned_node_no_seq删除当前节点
- 使用
-
以新的node_no_seq生成一个new_sol,并计算new_sol的属性
-
返回new_sol
搜索最大贡献值
def findRegretInsert(unassigned_node_no_seq,assigned_node_no_seq,model):
opt_insert_node_no = None
opt_insert_index = None
opt_insert_cost = -float('inf')
for node_no in unassigned_node_no_seq:
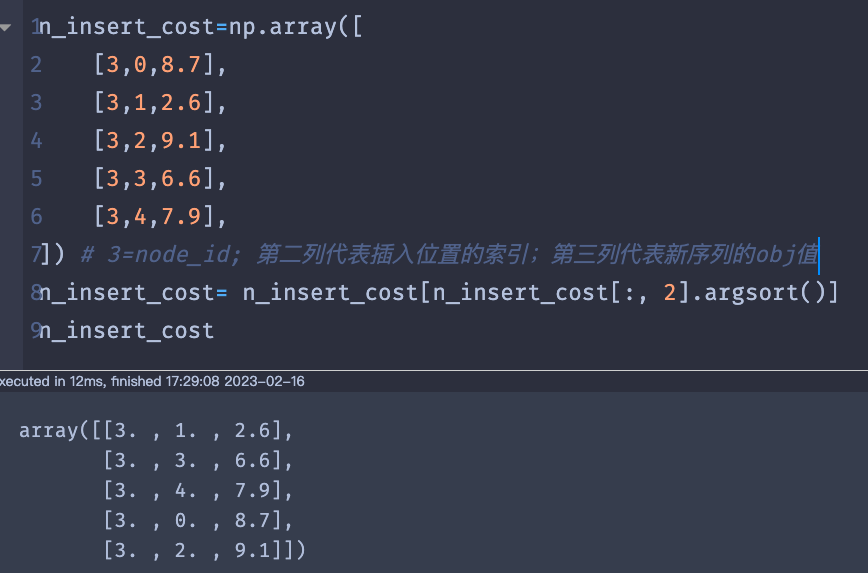
n_insert_cost=np.zeros((len(assigned_node_no_seq),3))
for i in range(len(assigned_node_no_seq)):
assigned_node_no_seq_=copy.deepcopy(assigned_node_no_seq)
assigned_node_no_seq_.insert(i,node_no)
obj_,_,_,_=calObj(assigned_node_no_seq_,model)
n_insert_cost[i,0]=node_no
n_insert_cost[i,1]=i
n_insert_cost[i,2]=obj_
n_insert_cost= n_insert_cost[n_insert_cost[:, 2].argsort()]
deta_f=0
for i in range(1,model.regret_n):
deta_f=deta_f+n_insert_cost[i,2]-n_insert_cost[0,2]
if deta_f>opt_insert_cost:
opt_insert_node_no = int(n_insert_cost[0, 0])
opt_insert_index=int(n_insert_cost[0,1])
opt_insert_cost=deta_f
return opt_insert_node_no,opt_insert_index
- model.regret_n = 5 # 后悔值破坏数量
- opt_insert_node_no = None ,最优插入节点
- opt_insert_index = None ,最优插入索引
- opt_insert_cost = -float(‘inf’),最优插入成本
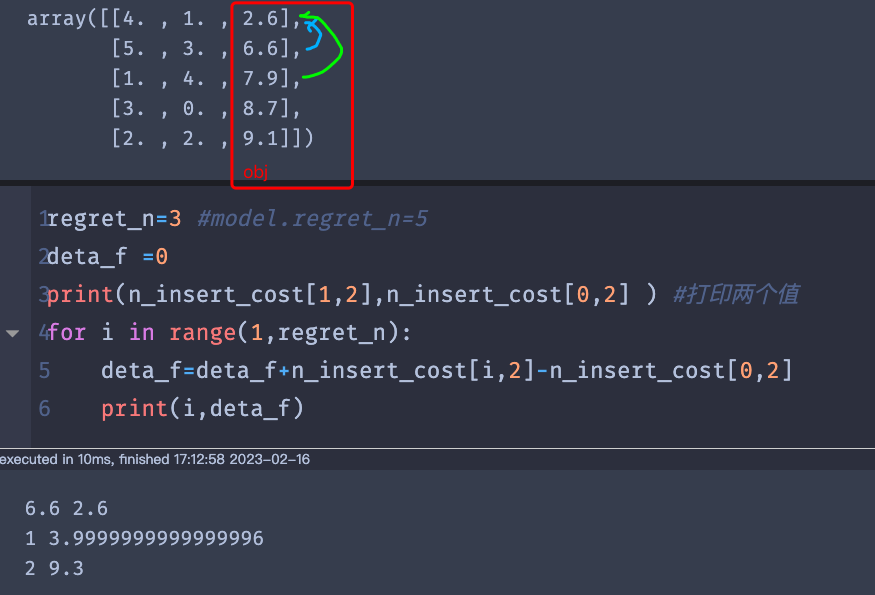
一. 对于未分配的节点进行循环,节点:node_no, 循环次数为:未分配的节点个数
1. n_insert_cost, 插入成本空矩阵,shape=(已分配节点个数,3)
2. 对于插入的位置进行循环,索引:i, 循环次数为:未分配的节点个数+1
1) assigned_node_no_seq_:已分配节点序列的 ’深复制‘
2) 按照循环的索引位置,将节点插入
3)计算新序列 assigned_node_no_seq_的obj_值
4) n_insert_cost中填入(i,0)--node_no ,(i,1)--i, (i,2)--obj_
3. n_insert_cost,计算最小插入成本
4. deta_f: 目标值的增幅,初始设为0
5. i:1->5的循环
i=1: deta_f=0+n_insert_cost[1,2]-n_insert_cost[0,2]
i=2:deta_f=n_insert_cost[1,2]-n_insert_cost[0,2]+ n_insert_cost[2,2]-n_insert_cost[0,2]
i=3: deta_f=n_insert_cost[1,2]-n_insert_cost[0,2]
+ n_insert_cost[2,2]-n_insert_cost[0,2]
+ n_insert_cost[3,2]-n_insert_cost[0,2]
i=4: deta_f =n_insert_cost[1,2]-n_insert_cost[0,2]
+ n_insert_cost[2,2]-n_insert_cost[0,2]
+ n_insert_cost[3,2]-n_insert_cost[0,2]
+ n_insert_cost[4,2]-n_insert_cost[0,2]
6. Dudge: regret_n个增幅值的和> 最优插入成本
更新最优插入节点id
更新最优插入节点的索引
更新最优插入节点的obj
二、return : opt_insert_node_no,opt_insert_index
对于一个待插入的序列和一个需要插入的节点。
我们计算假设在每个索引插入后的新序列(们)的obj值。根据obj值从小到大获得插入索引的排序。选中较小的obj值的前regret_n=5个,累计后4个与最小obj的增幅值求和,为deta_f.并将deta_f与最优插入成本n_insert_cost作比较,然后选择是否更新n_insert_cost.
注意:这里做比较不是选择的是最小的obj值,为什么如此设计的原因未知!!!
2.4 执行修复算子
def doRepair(repair_id,reomve_list,model,sol):
if repair_id==0:
new_sol=createRandomRepair(reomve_list,model,sol)
elif repair_id==1:
new_sol=createGreedyRepair(reomve_list,model,sol)
else:
new_sol=createRegretRepair(reomve_list,model,sol)
return new_sol
- repair_id: 0-1-2随机数,当前有3种修复方式
随机修复:基于解sol,随机产生插入索引,随机插入节点
贪婪修复:对于选择的节点和插入的位置,使得obj增幅最高即可的一组索引和节点
最值修复:对于选择的节点和插入的位置,使得后续插入的obj增长最高的一组索引和节点
三。选择–破坏and修复的类型
def selectDestoryRepair(model):
d_weight=model.d_weight
d_cumsumprob = (d_weight / sum(d_weight)).cumsum()
d_cumsumprob -= np.random.rand()
destory_id= list(d_cumsumprob > 0).index(True)
r_weight=model.r_weight
r_cumsumprob = (r_weight / sum(r_weight)).cumsum()
r_cumsumprob -= np.random.rand()
repair_id = list(r_cumsumprob > 0).index(True)
return destory_id,repair_id
- model.d_weight=d_weight = np.ones(2) * 10 =array([10.10]) # 破坏算子权重
- np.random.rand() 每一个元素是服从0~1均匀分布的随机样本值,也就是返回的结果中的每一个元素值在0-1之间。
- model.r_weight=np.ones(3) * 10 =array([10,10,10) # 修复算子权重
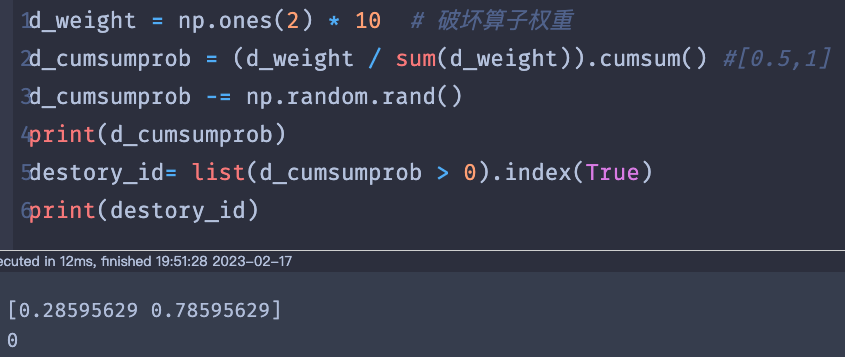
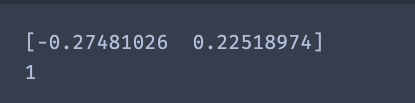
return:
- 对于破坏算子会随机返回0或1;
- 对于修复算子会随机返回0,1,2
更新算子权重
在electDestoryRepair中可以看到选择破坏算子或者修复算子是被model.d_weight和model.r_weight的值影响的.所以,改变该数组值则会影响选择结果.因此,有了该函数.
def updateWeight(model):
for i in range(model.d_weight.shape[0]):
if model.d_select[i]>0:
model.d_weight[i]=model.d_weight[i]*(1-model.rho)+model.rho*model.d_score[i]/model.d_select[i]
else:
model.d_weight[i] = model.d_weight[i] * (1 - model.rho)
for i in range(model.r_weight.shape[0]):
if model.r_select[i]>0:
model.r_weight[i]=model.r_weight[i]*(1-model.rho)+model.rho*model.r_score[i]/model.r_select[i]
else:
model.r_weight[i] = model.r_weight[i] * (1 - model.rho)
model.d_history_select = model.d_history_select + model.d_select
model.d_history_score = model.d_history_score + model.d_score
model.r_history_select = model.r_history_select + model.r_select
model.r_history_score = model.r_history_score + model.r_score
- model.d_weight=array([ , ]) #破坏算子的权重
- model.d_select =array([ , ]) # 破坏算子选择次数
- model.d_score=array([ , ]) # 破坏算子的得分
- model.d_history_select=array([ , ]) # 破坏算子累计选择次数
- model.d_history_score =array([ , ])# 破坏算子累计得分
- model.rho # 权重衰减哔哩
- model.r_weight=array([ , , ])
- model.r_select=array([ , , ])# 修复算子选择次数
- model.r_score==array([ , , ])# 修复算子的得分
- model.r_history_select=array([ , , ])# 修复算子累计选择次数
- model.r_history_score=array([ , , ])# 修复算子累计得分
初始情况
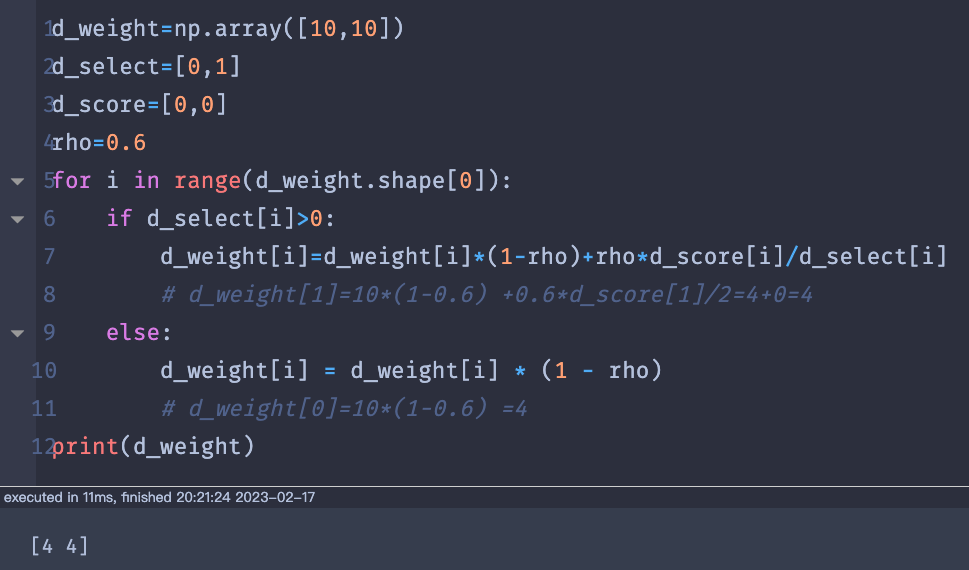
一般情况
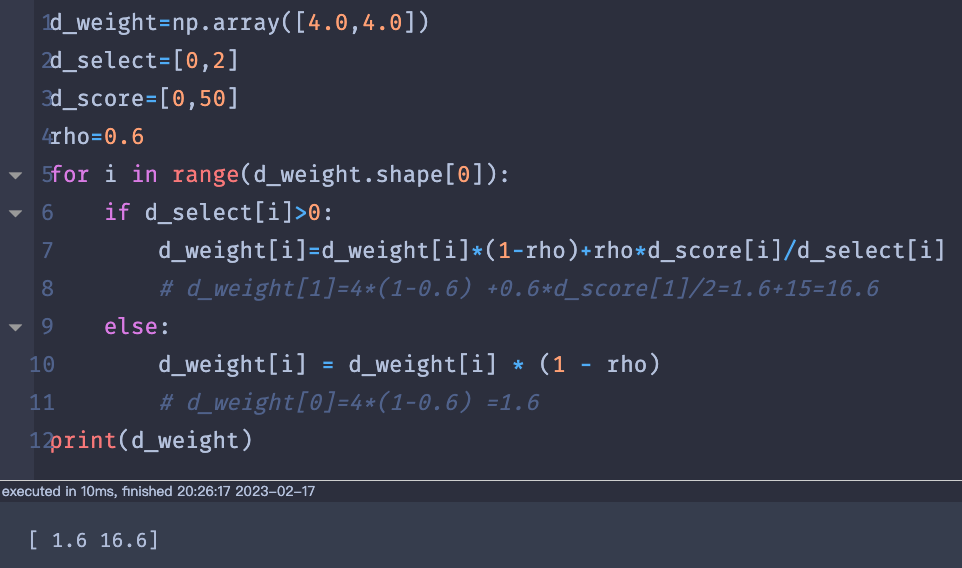
与d_score相关.d_score的值与主函数的下面代码相关.
# model.r1=30, model.r2=20, model.r3=10
if new_sol.obj<sol.obj:
sol=copy.deepcopy(new_sol)
if new_sol.obj<model.best_sol.obj:
model.best_sol=copy.deepcopy(new_sol)
model.d_score[destory_id]+=model.r1 #一等得分值
model.r_score[repair_id]+=model.r1
else:
model.d_score[destory_id]+=model.r2 #二等得分值
model.r_score[repair_id]+=model.r2
elif new_sol.obj-sol.obj<T:
sol=copy.deepcopy(new_sol)
model.d_score[destory_id] += model.r3 #三等得分值
model.r_score[repair_id] += model.r3
new_sol是在sol上破坏和修复后的新领域解.
- 情况一: 新解的obj<原解的obj + 新解的obj<最优解的obj==>得30分
- 情况2: 新解的obj<原解的obj, 但没有比最优解好==》得20分
- 情况3:新解比原来的解差==》得10分.
重置得分
在每个epoch中重置得分的初始值.因为会出现比[1.6, 16.6]两者之间的差距跟大的值.如果这样的值一直出现,则失去了选择破坏算子和修复算子的初衷,这样就不是ALNS与LNS没啥大的区别了.
def resetScore(model):
model.d_select = np.zeros(2)
model.d_score = np.zeros(2)
model.r_select = np.zeros(3)
model.r_score = np.zeros(3)